Homework #3: BME 2210
Due as a single PDF file ICON submission by Friday, September 28, 2018 by 5:00 PM
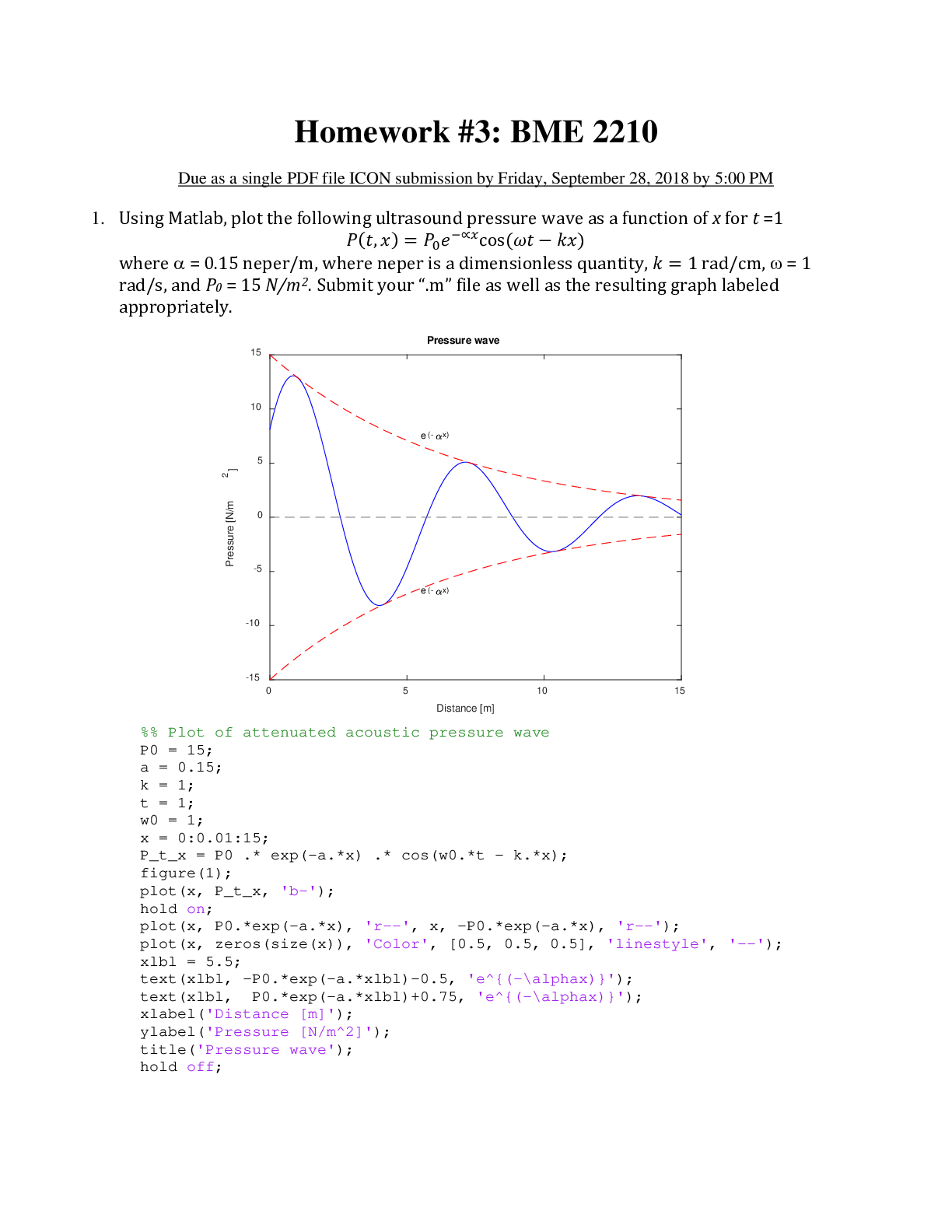
1. Using Matlab, plot the following ultrasound pressure wave as a function of x for t =1
??(??, ??) = ??0??−∝??co
...
Homework #3: BME 2210
Due as a single PDF file ICON submission by Friday, September 28, 2018 by 5:00 PM
1. Using Matlab, plot the following ultrasound pressure wave as a function of x for t =1
??(??, ??) = ??0??−∝??cos(???? − ????)
where α = 0.15 neper/m, where neper is a dimensionless quantity, ?? = 1 rad/cm, ω = 1
rad/s, and P0 = 15 N/m2. Submit your “.m” file as well as the resulting graph labeled
appropriately.
%% Plot of attenuated acoustic pressure wave
P0 = 15;
a = 0.15;
k = 1;
t = 1;
w0 = 1;
x = 0:0.01:15;
P_t_x = P0 .* exp(-a.*x) .* cos(w0.*t - k.*x);
figure(1);
plot(x, P_t_x, 'b-');
hold on;
plot(x, P0.*exp(-a.*x), 'r--', x, -P0.*exp(-a.*x), 'r--');
plot(x, zeros(size(x)), 'Color', [0.5, 0.5, 0.5], 'linestyle', '--');
xlbl = 5.5;
text(xlbl, -P0.*exp(-a.*xlbl)-0.5, 'e^{(-\alphax)}');
text(xlbl, P0.*exp(-a.*xlbl)+0.75, 'e^{(-\alphax)}');
xlabel('Distance [m]');
ylabel('Pressure [N/m^2]');
title('Pressure wave');
hold off;
0 5 10 15
Distance [m]
-15
-10
-5
0
5
10
15
Pressure [N/m 2
]
Pressure wave
e (- x)
e (- x)
2. An ultrasound imaging system is used to create a B-mode image of a soft-tissue sample. We
want an image that extends to a depth of 30 cm from the transducer. Assume that 175
A-mode lines are used to create the B-mode image.
a) How much time is required to acquire the data for each A-mode line?
Assume that the speed is constant and equals 1540 m/s.
Since it is not given, pulse time can be ignored.
????−???????? = ??
?? = 0.3 × 2
1540 = 390 ????????
b) What is the maximum possible B-mode image refresh rate, in frames per second?
???????????? = ????−???????? × ???????????? = 390 × 175 = 68.25 ????????
Therefore maximum frame rate (FR) becomes:
???? = 1
????????????
= 14.65 ?????????? ?????? ????????????
c) Using the same refresh rate calculated above, what is the maximum depth possible if all
A-mode lines are acquired simultaneously?
If all lines are acquired simultaneously, the frame time will be the same as a single line
time:
???????????? = ????−???????? = 68.25 ????????
????????ℎ = ?? × ????????????
2 = 52.55 ??
Of course this is not realistic since the signal will be attenuated several centimeters from
the transducer.
3. Answer the following showing your work:
a) If the attenuation coefficient of the heart muscle ??ℎ?? = 0.185 (???? ∙ ??????)−1, calculate
the distance at which the signal amplitude of a 2-MHz ultrasound beam will be reduced
by half traveling through heart muscle.
b) You have two transducers available, a 25-MHz transducer and a 3-MHz transducer.
Which transducer should you use to perform an echocardiogram, and why (show your
work)?
Our model for the pressure (or intensity) P(t) of an ultrasound wave passing through the
body is:
??(??) = ??0 (??)??−??????????(???? − ????)
where the attenuation is given by ??−????. The value of z when the intensity is one-half of
the initial intensity (due to attenuation) is then when
??−???? = 1
2
→ ln(0.5) = −????
with ??ℎ?? = 0.185 × 2 = 0.37????−1, solving for ?? yields ?? = 1.87????.
We know that the attenuation coefficient ?? varies linearly with frequency ??, therefore,
??ℎ??3?????? = 0.185 × 3 = 0.555 ????−1, which means signal is reduced by half after
?? = 1.25????.
On the other hand, ??ℎ??_25?????? = 0.185 × 25 = 4.625 ????−1, which means that the
signal is reduced by half after ?? = 0.15????.
So the best transducer for interrogating the heart is the 3-MHz transducer. The 25-MHz
transducer has too much attenuation at the deep core structures.
4. An ultrasound beam incident at an angle of 15° from fat tissue into muscle tissue, calculate
the angle of refraction using the table below?
Material Density
[kg/m3
]
Acoustic
Impedance
[kg.m-2
.s-1
]
Attenuation
Coefficient (α)
[neper.m-1
.MHz-1
]
Fat 920 1.35 x 106 1.072
Muscle 1070 1.68 x 106 1.46
Water 1000 1.52 x 106 1.0
Snell’s law states:
sin ????
sin ????
= ??1
??2
Also we have ?? = ??0??, therefore,
Cfat = (1.35x106
) / (920) = 1467 m/s
Cmuscle = (1.68x106
) / (1070) = 1570 m/s
sin ???? = ??????????????
????????
× sin ???? = 1570 × sin(15°)
1467
???? = 16.1°
5. Using the table above and in the figure shown below, the transducer is stimulated with a
A B
Fat Muscle
Transducer
Water
short pulse resulting in a short burst of pressure traveling through the sequence of materials
shown in figure. Assume that no echoes are returned at the transducer-tissue interface. The
transducer is operating at 3 MHz frequency, measured from the transducer edge, A = 3 cm
and B = 5 cm. Use specific sound speeds in the corresponding materials.
a) Assuming perpendicular incidence and that the system is setup to equalize the amplitude
of all the returned signals (don’t account for attenuation and reflection/transmittance at
interfaces), sketch the timing of the first echoes (signals) received by the transducer
from interfaces A, and B.
Since speeds can be calculated from table above, we have
Cfat = (1.35x106
) / (920) = 1467 m/s
Cmuscle = (1.68x106
) / (1070) = 1570 m/s
tA = dtravel/cfat = 2x3x10-2 / 1467 = 40.9 µsec.
tB = tA + dtravel/cmuscle = 40.9x10-6 + (2x2x10-2 / 1570) = 66.4 µsec.
b) Now accounting for attenuation and reflection/transmittance at interfaces calculate the
actual amplitudes of the pulses from interfaces A and B relative to the incident
amplitude.
Since attenuation is a function of frequency, therefore at f = 3 MHz we have:
???????? = 1.072 ∗ 3 = 3.216 ??????????
??
Attenuation factor due to fat (one way travel) = ??−???????????????? = ??−3.216∗0.03 = 0.908
?????????????? = 1.46 ∗ 3 = 4.38 ??????????/??
Attenuation factor due to muscle (one way travel) = ??−???????????????????????????? = ??−4.38∗0.02 = 0.916
Also we have,
????????−???????????? = �
?????????????? − ????????
?????????????? + ????????
� = 0.109
??????????????−?????? = �
???????? − ??????????????
?????????????? + ????????
� = −0.109
Time
Pressure
40.9 µsec 66.4 µsec
P0 P0
??????????????−?????????? = �
???????????? − ??????????????
?????????????? + ????????????
� = −0.05
????????−???????????? = � 2 × ??????????????
?????????????? + ????????
� = 1 + ????????−???????????? = 1.109
??????????????−?????? = � 2 × ????????
?????????????? + ????????
� = 1 + ??????????????−?????? = 0.891
???? = ??0 × ??−???????????????? × ????????−???????????? × ??−????????????????
= ??0(0.908)(0.109)(0.908) = 0.09??0
???? = ??0 × ??−???????????????? × ????????−???????????? × ??−???????????????????????????? × ??????????????−??????????
× ??−???????????????????????????? × ??????????????−?????? × ??−????????????????
= ??0(0.908)(1.109)(0.916)(−0.05)(0.916)(0.891)(0.908) = 0.034??0
Time
Pressure
40.9 µsec 66.4 µsec
PA = 0.09 P0
PB = 0.034 P0
[Show More]







.png)


 HESI VI EXIT EXAM.png)






















