StarGuard Written Test Review – 100% Correct Answers | Verified | Latest 2024 Version
$ 9.5

TEST BANK for BUSINESS RESEARCH METHODS 5th Edition by Emma Bell, Alan Bryman and Bill Harley ISBN-13 978-0198809876. (Complete Chapters 1-27).
$ 22
 – Chamberlain College of Nursing.png)
MATH 225N Week 5 Lab Assignment (2020) – Chamberlain College of Nursing | MATH225N Week 5 Lab Assignment (2020)
$ 6.5

PSYC 426 Athabasca University Final Exam questions and answers with 100% correct answers 2024
$ 15.5

2023/2024 ATI TEAS 7 READING LATEST VERSION 45 QUESTIONS & ANSWERS.
$ 20

GCE Computer Science H446/01: Computer systems A Level Mark Scheme for June
$ 10.5

Sociology2001 > SOCL 2001 / SOCL2001 Sociology test bank
$ 8.5
.png)
Humanities through the Arts 10th Edition by Lee Jacobus, F. David Martin
$ 7

PN ADULT MEDICAL SURGICAL ONLINE PRACTICE 2024 A AND B WITH NGN
$ 32.5

HESI Exponents Practice Test Question Answers
$ 10

Sophia Learning Art History 1 – Unit 3 Milestone 3,100% CORRECT
$ 13

Agile E1 (CBO) 60566 ‘’Questions and Answers 100% guarantee answers aid grade A’’
$ 8.5
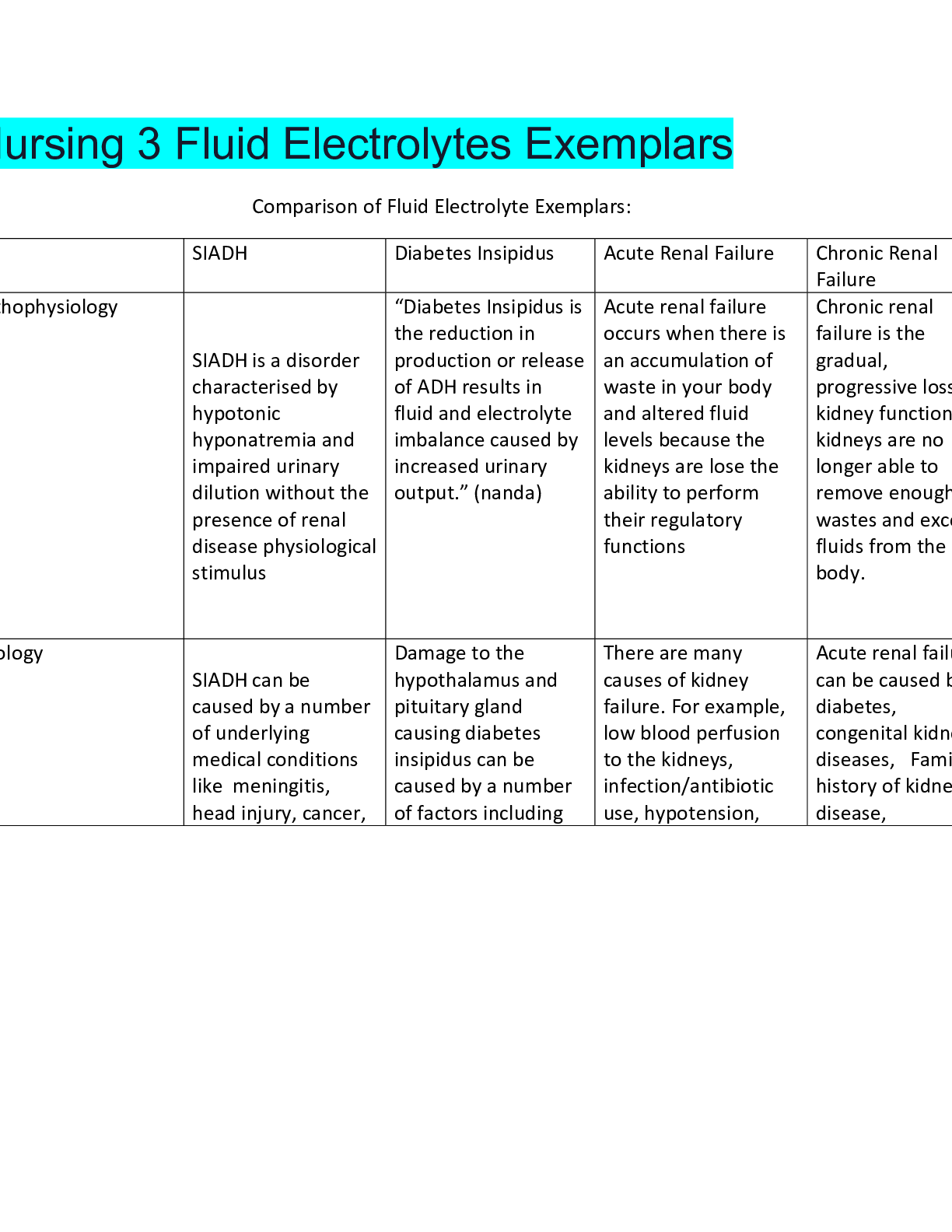
Nursing 3 Fluid Electrolytes Exemplars,100% CORRECT
$ 11

CS 1101 Programming Fundamentals - Term 3, 2021-2022
$ 12

The City College of New York, CUNY MECHANICAL ENGINEERING<<<ME 46100Lab 11 461-5
$ 8

NEW NURS 6670 midterm exam 2023 (MAY-JULY SESSION) –Walden University Questions with Answers, Updated file 2023 JUNE
$ 12.5

NURSE AIDE PRACTICE TEST EXAM COMPLETE QUESTIONS WITH CORRECT ANSWERS GUARANTEED PASS | RATED A+
$ 9.5

AST 113 ASTRONOMY Lab 9
$ 9

Selected Harry George (Room 401) Quiz | Lesson 22 | Diabetes Mellitus, Part 1 2022
$ 17.5

MVA LEANERS PERMIT TEST 100% CORRECT
$ 12

NR-103 Week 5 RUA Assignment Compassion Fatigue The Cost of Caring (Complete)
$ 7

ATI Proctored Mental Health
$ 12

HESI EXIT ADVANCED PATHOPHYSIOLOGY 2023 COMPLETE EXAM QUESTIONS AND VERIFIED ANSWERS – EXPERT FEEDBACK
$ 11

Star Spectra Gizmo
$ 7

SOCS 325 Week 8 Final Exam
$ 38

eBook [PDF] Women Moralists in Early Modern France 1st Edition By Julie Candler Hayes
$ 29

[Solved] As an alternative proposal means of increasing shareholder value
$ 14

Ashford University - MAT 232MAT232 WEEK4 DISCUSSION1
$ 7

eBook Affect and Emotion in Multi-Religious Secular Societies 1st Edition By Christian von Scheve, Anna Berg, Meike Haken, Nur Ural
$ 29

DAANCE ALL MODULE EXAM GUIDE 2023 SOLUTION WELL ANSWERED.
$ 12

NR 603 Week 5 APEA Predictor Assignment
$ 5

Case Study: 100 Yen Sushi _ QSO-610-11376-M01 Mgmt of Service Operations | Answered correctly Latest 2026 updated.
$ 13

Test Bank for Fundamentals of Physics 10th Edition by David Halliday, Resnick, Walker | All Chapters 1-44
$ 19

[eBook] (EPUB) [PDF] Biochemistry A Short Course 5th Edition By Justin Hines, Catherine Reinke, John Tymoczko
$ 30

eBook Standorttheorien, Regional- und Stadtökonomik in Theorie und Praxis, German Edition 1st edition by Oliver Farhauer, Alexandra Kröll
$ 29

AQA A-level CHEMISTRY 7405/1 JUNE 2022 FINAL MARK SCHEME> Inorganic and Physical Chemistry
$ 17

Ashford University - MATH MAT 232MAT 232 week 4 discussion.
$ 7

ITS 462 - Colorado State University. The Module 3 reading covers the CISA stages of the audit process. A CISA is expected to have a thorough understanding of the entire audit process. Choose two of the 10 stages (listed below), and describe each chosen stage and its importance to the overall auditing process.
$ 9.5

ATI COMPREHENSIVE EXIT FINAL (summer 2024)
$ 14

Auditing & Assurance Services, 7th Edition by Grant Gay | TEST BANK
$ 26

CS 1101 Programming Fundamentals - Term 5, 2021-2022
$ 11

BILLY JOHNSON iHuman Case Study. Complete Solution
$ 10

USPS Exam 421 Window Clerk
$ 10

[eTextBook] [PDF] Foundations of Mechanical Accuracy 1st Edition By Wayne R. Moore
$ 29
.png)
WGU C790 NURSING INFORMATICS QUESTIONS AND ANSWERS 100% CORRECT
$ 10.5

Feel the Heat, Student Exploration | Questions and Answer Key GIZMOS
$ 6

WGU Masters Course C795 - Cybersecurity Management II Tactical
$ 18

PEARSON EDEXCEL A LEVEL JUNE 2023 JAPANESE QUESTION PAPER 1
$ 7

AQA A-level COMPUTER SCIENCE Paper 1 QP 2021
$ 10

NRS 433 Topic 2 DQ 2
$ 7

ATI_NCLEX PREDICTOR REMEDIATION STUDY NOTES (New, 2020) (SATISFACTION GUARANTEED
$ 30

2020_OCR_COMPUTER_SCIENCE_2_PRO_MS.pdf (1)
$ 13

Test Bank for Principles of Auditing and Other Assurance Services 22nd Edition by Ray Whittington and Kurt Pany
$ 24

OCR GCE Computer Science H446/02: Algorithms and programming Advanced GCE Mark Scheme for Autumn 2021
$ 10

Research Paper > ACS College of Engineering - MATH. 1014. Polar coordinate system
$ 12

SOCS 185N Week 5 Assignment: Pre-Writing Map for the You Decide Census Paper
$ 9
.png)
AAPC - Final Exam
$ 10
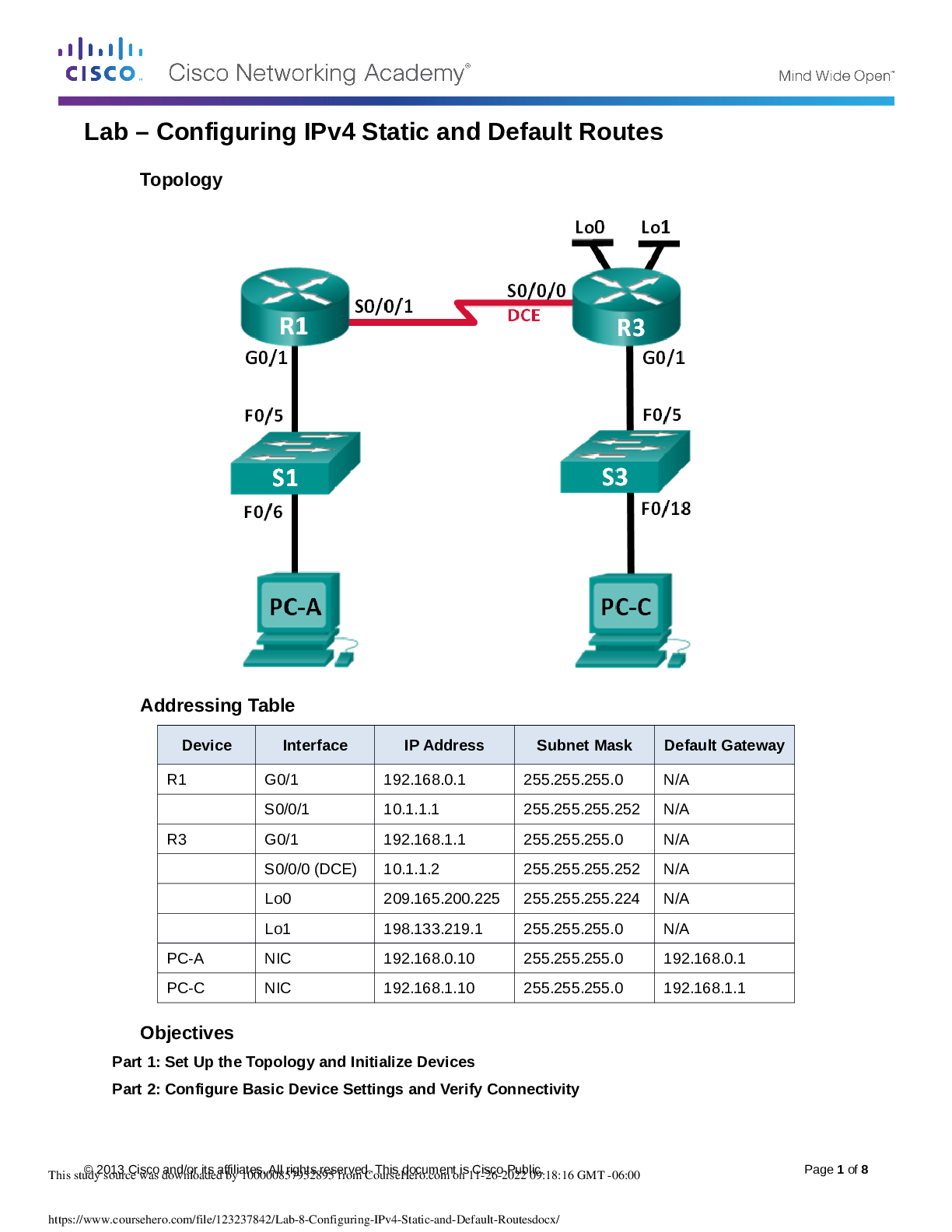
Lab 8 - Configuring IPv4 Static and Default Routes.





 (Diane Pacitti etc.png)