Tutorial: UDFs for a User-Defined Scalar
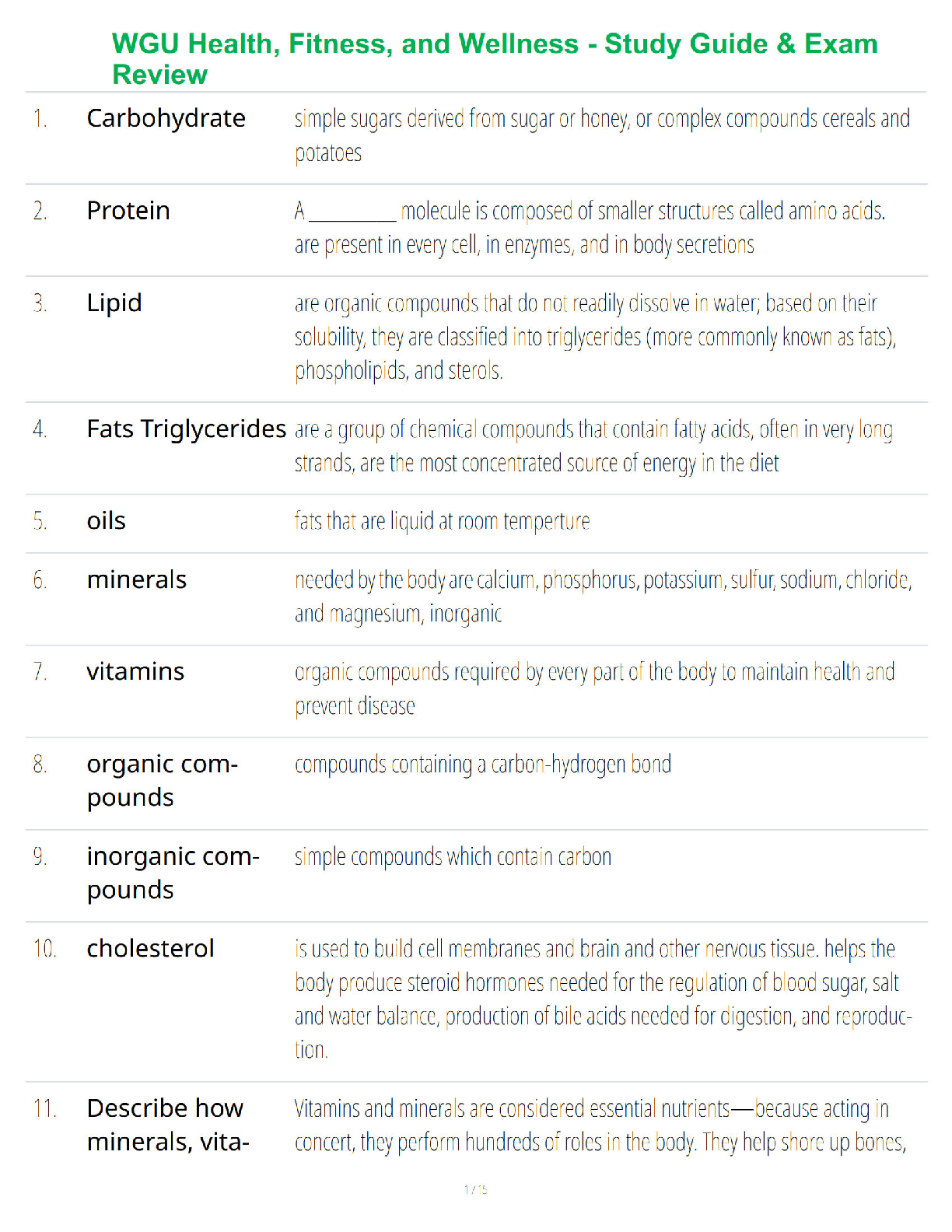
Introduction
ANSYS FLUENT solves the the transport equation for a user-defined scalar (UDS) in the
same way as it solves the transport equation for a scalar in the core equatio
...
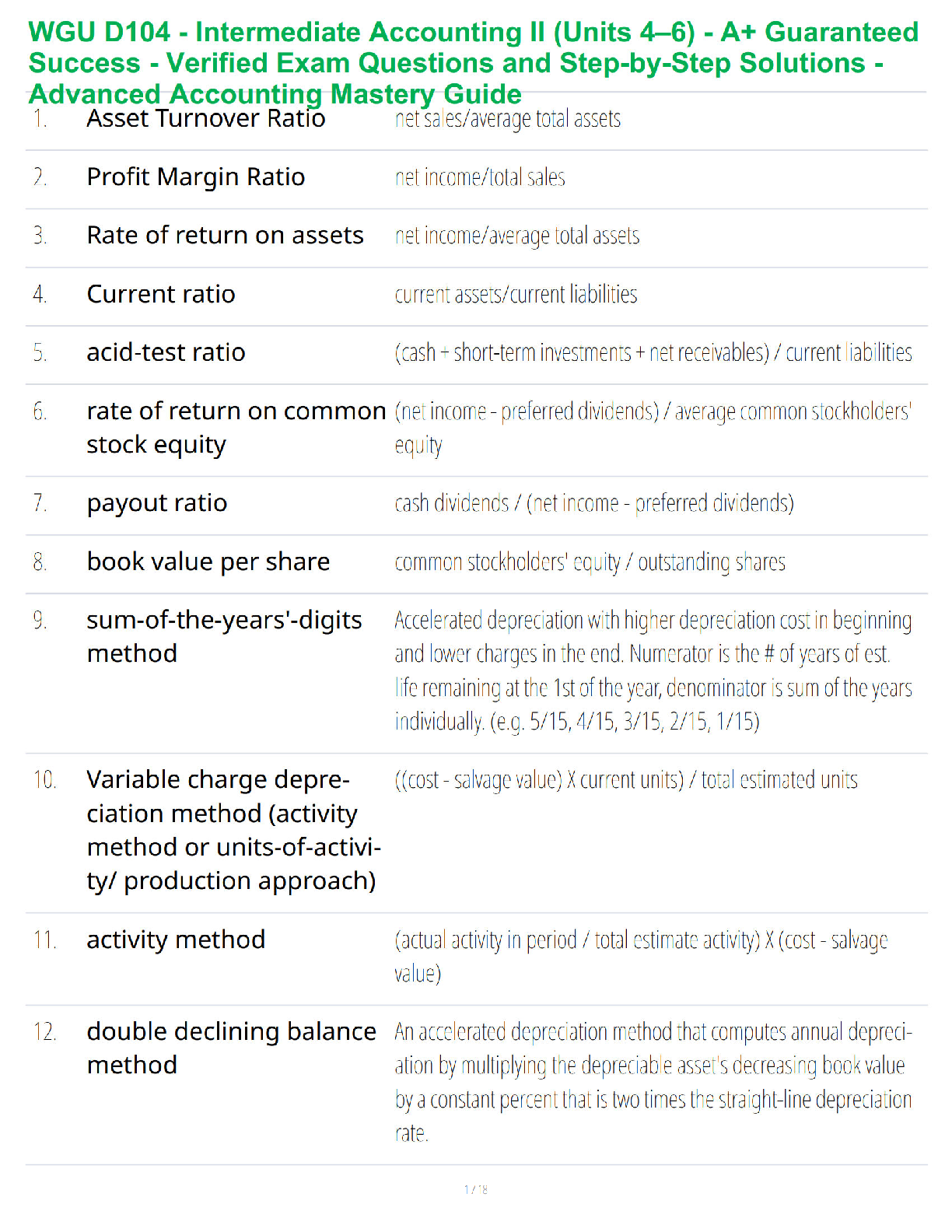
Tutorial: UDFs for a User-Defined Scalar
Introduction
ANSYS FLUENT solves the the transport equation for a user-defined scalar (UDS) in the
same way as it solves the transport equation for a scalar in the core equations, such as
a species mass fraction. The UDS capability can be used to implement a wide range of
physical models in magnetohydrodynamics, electromagnetics, and more.
In this tutorial you will learn to solve a general scalar diffusion equation (1) with the
possible types of boundary condition (BC) at the boundary (or a part of the boundary) of
the domain.
c
@φ
@t − r: (Γrφ) = Sφ; in Ω; t > 0 (1)
The possible types of boundary conditions are as follows:
• Dirichlet BC: φ = D0
• Neumann BC: −Γ(@φ=@n) = q0
• Mixed BC: −Γ(@φ=@n) = hc(φ − φ1)
Here, D0, q0, hc, and φ1 are constant values.
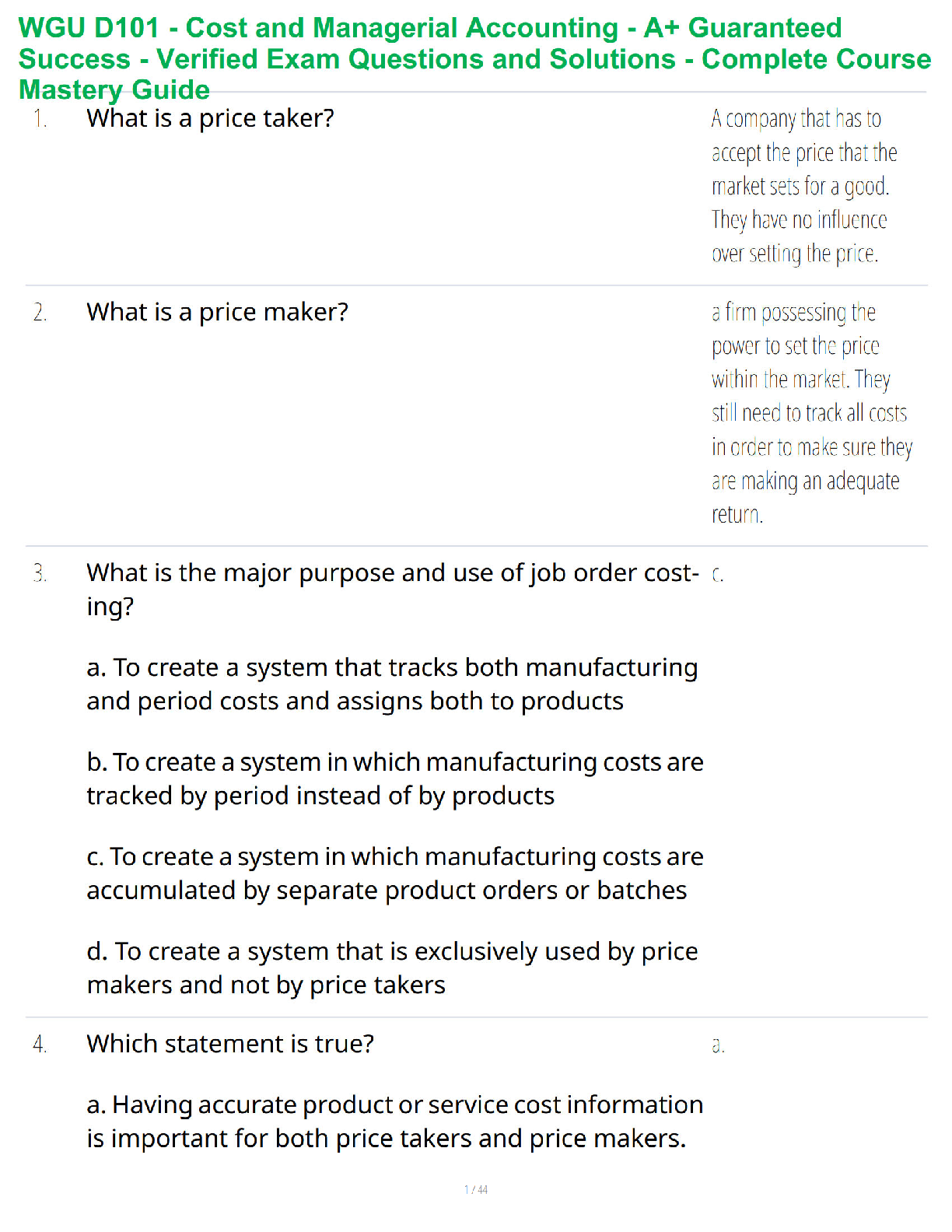
Prerequisites
This tutorial is written with the assumption that you have completed Tutorial 1 from
ANSYS FLUENT 12.0 Tutorial Guide, and that you are familiar with the ANSYS FLUENT
navigation pane and menu structure. Some steps in the setup and solution procedure will
not be shown explicitly.
For more details about UDFs, see ANSYS FLUENT 12.0 UDF Manual.
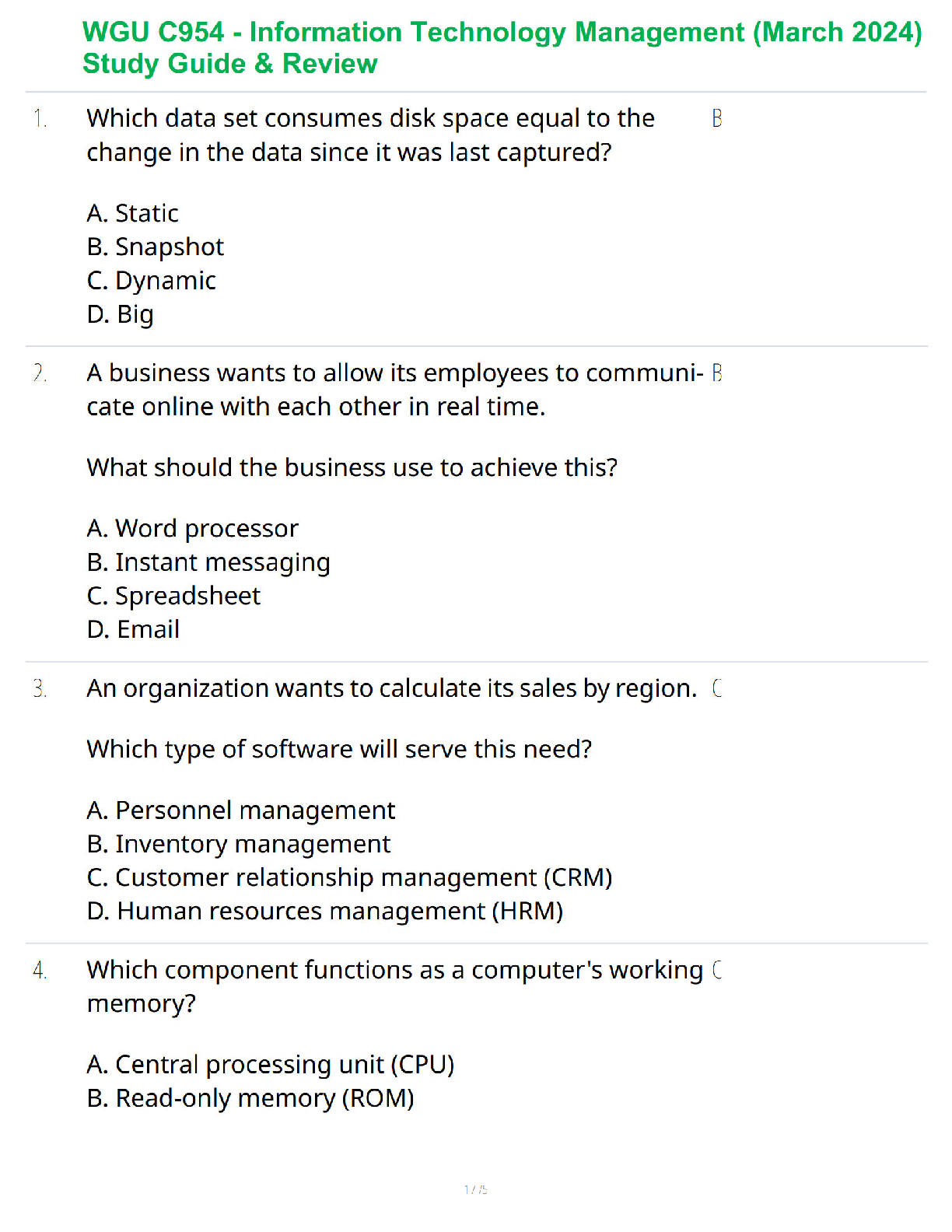
Problem Description
As shown in the problem illustration, the problem is a 2D rectangle, with constant flux,
constant value, and mixed boundary conditions along the boundary edges.
[Show More]