5 Hooke’s Law
Introduction
When a net force F is applied to a spring, it will stretch or compress the spring by a distance Δx.
Where k is called the spring constant and is a measure of the stiffness of the spring. I
...
5 Hooke’s Law
Introduction
When a net force F is applied to a spring, it will stretch or compress the spring by a distance Δx.
Where k is called the spring constant and is a measure of the stiffness of the spring. In this
equation ( -^ x ̂) represents that force and displacement is in opposite direction to each other.
Force and the displacement display a linear relationship.
The graph of Force vs displacement is a linear graph in
the form of y= mx. Now, we have (ideally) the slope (m) =
k (spring constant).
Pre-lab and Discussion Questions
Pre-Lab Questions
This part of the lab is to be completed prior to class.
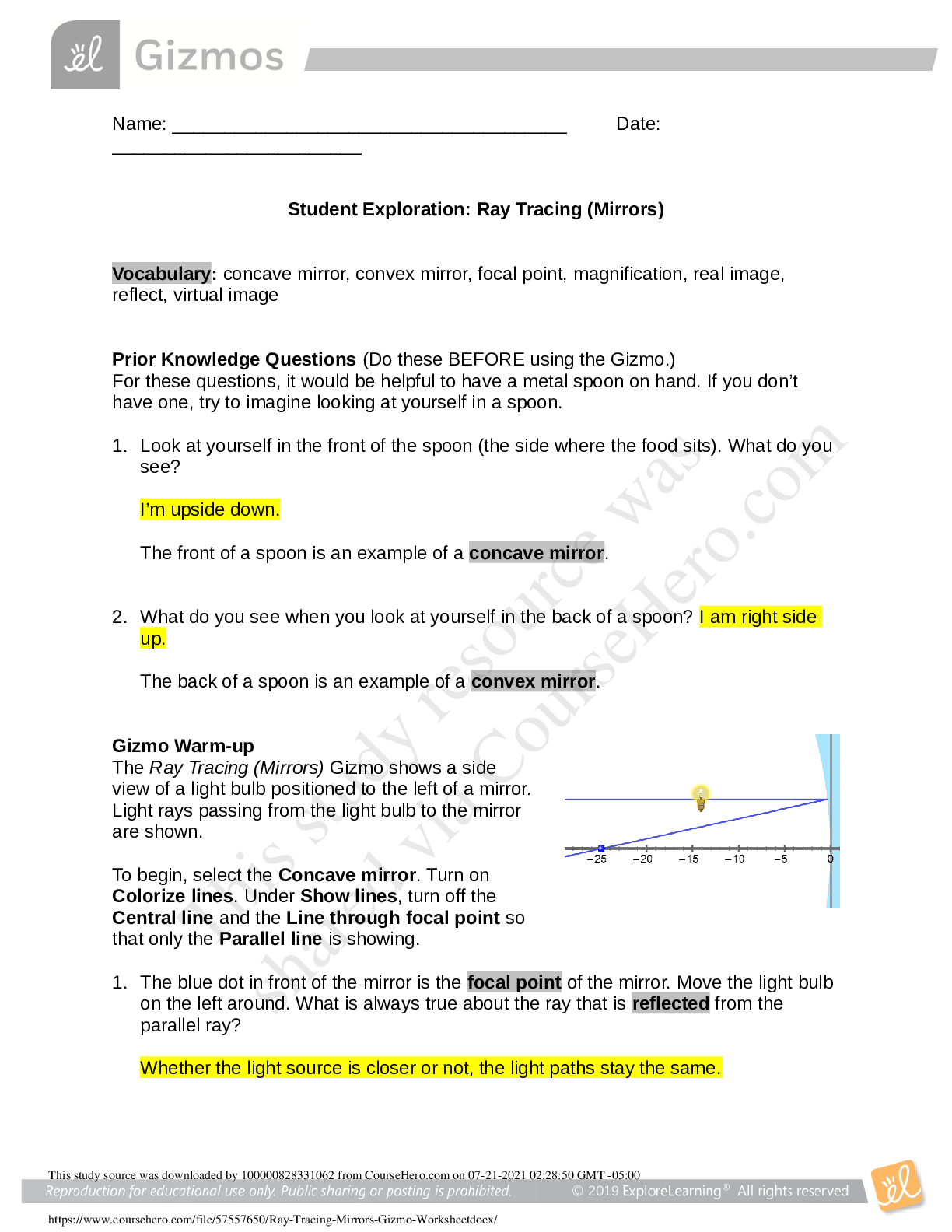
All springs have an inherent length when they are in equilibrium, and we set this as x = 0.
1. Why do you think a force is generated when a spring is stretched or compressed? [3 pts]
2. How does the direction of the force change when a spring is
compressed (x < 0) or stretched (x > 0). Why this force is
called a restoring force? [3 pts]
3. A spring is characterized by a constant k that measures its stiffness. How does the restoring
force depend on k? [3 pts]
4. A force of 600 N compresses a spring by 0.5 m. What is the spring constant for this spring?[3
pts]
5. A force of 40 N will stretch a spring by 0.1 m. How far will a force of 80 N stretch it? [3 pts]
Discussion Questions
This part of the lab is to be completed with your group in class.
Hooke’s Law can also be applied to a spring hanging vertically.
Like a horizontal spring, we call the equilibrium point x = 0.
6. What new force should be taken into account for this situation? [3 pts]
7. Draw a free-body diagram and find an expression for the equilibrium position x. [3
pts]
8. Hooke’s Law states that the distance a vertical spring stretches varies directly with the weight
hanging from it. A spring stretches 35 cm when a 3 kg mass is hanging from it. What is the
mass needed to stretch the spring 80 cm? [4 pts]
F W
Figure 1: Spring in natural length and stretched length
Experiment
The purpose of this lab is to verify Hooke’s Law and determine the spring constants for various
springs and combinations.
Equipment: The following simulators will be used in this experiment.
Part 1: https://phet.colorado.edu/sims/html/masses-and-springs/latest/masses-and-springs_en.html
Part 2: https://phet.colorado.edu/sims/html/hookes-law/latest/hookes-law_en.html
In those simulators, you will use springs with different spring constants.
Part 1: Verify Hooke’s Law using a vertically hanging spring.
• Open the https://phet.colorado.edu/sims/html/masses-and-springs/latest/masses-andsprings_en.html and open the LAB link.
• Click Displacement/ Natural length, and mass equilibrium to display those lines on the
simulator screen.
• Keep the gravity as 9.8 m/s2 (earth gravitational acceleration).
• Set the damping factor as LOTS. This will help you to read the equilibrium position easily.
Note that it will not affect the stretch length on the simulator.
• Set the spring constant LARGE.
• Drag the ruler to the simulator screen and place it at the natural length indicator (blue dash
line) on zero.
• Open Excel and construct a table with the headings shown in Table 1. The table should
include a title, column headings with units.
Table 1: The table of hanging mass, force and displacement [5 pts]
Hanging mass (kg) Force (N) Displacement (m)
• The displacement of the spring is the
distance between the natural positions
(Blue dash line) of the spring to the
equilibrium position (black dash line) as
shown in Figure 1. To exert a force on
the spring, add 50 g to the holder. Find
the displacement x of the spring (the
scale increments are 1 mm) and
record it in the spreadsheet in the appropriate column. Repeat, adding another 50 g each
time until you run out of masses.
•Fill in the mass increments on your table and then find the gravitational force F (N) acting on the
spring in each mass increment (hint: force = mass x gravity).
•Create a graph of Force vs. Displacement on excel. Add a linear trend line and display the
equation.
9. What type of relationship does Hooke’s Law predict between the force and the displacement?
Does your graph show this relationship? [5 pts]
10. What is the unit for the slope of your graph? Given this, how does the slope relate to the spring
constant k? What is the spring constant of the spring used in this simulator? [5 pts]
11. Insert a screenshot of your graph here or attach the excel file. [10 pts]
Part 2: Determine the spring constants for various spring combinations.
• Open the simulator at
https://phet.colorado.edu/sims/html/hookes-law/latest/hookes-law_en.html and open “systems”.
• Add a second sheet to the excel file and create a table with the following column headings:
Apply different forces from -100 to + 100 in increments of 25 (-100, -75, -50, -25, 0, +25, +50,
+75, +100) and record the displacement in the appropriate column.
Applied Force
(N)
Displacement for springs in parallel
(m)
Displacement for springs in series
(m)
• Now choose the series combination . Set spring constant as 400 N/m for both springs.
Record the displacement Δx of the series combination of springs for various applied forces.
12. Create a graph of Force vs displacement that includes the series combination of springs and
parallel combinations. The completed graph should have two scatter graphs. Make sure to plot
Force on the y-axis and displacement on the x-axis. Add a linear trendline to each scatter graph
and be sure to display the best-fit equation on the graph. Insert a screenshot of your table and
graph below, or attach the excel file. Note that your graph should include title, axis titles
(including units), scale, and a trend or fit line. [10 pts]
13. Record the value of the spring constant for the series and parallel combination in Data Table 3
as kexpt.
Data Table 3: Spring Constants [5 pts]
Slope k (N/m)
Single Spring: 400 400
Springs in parallel: 800 800
Springs in series: 200 200
• Suppose we wanted to replace the series combination of springs with a single spring that has
an equivalent spring constant. In physics, the characteristics of items combined in series
usually follow one of two relationships:
14. Using your experimental data, determine which formula is correct for adding springs in series.
15. Two springs added in series will always have a LARGER / SMALLER final spring constant
than either of the individual springs. (Circle the correct answer.) [2 pts]
16. Each spring has set to have a spring constant of 400 N/m. Calculate the theoretical value of the
spring constant for the series and parallel combination using the given equation above. Record
17. Calculate the percent error between the experimental and theoretical values of kSeries and the
percent error between the experimental and theoretical values of kparallel. Record in Data Table
4. Show an sample calculation below. [5 pts]
Results and Conclusions (10 pts)
Briefly summarize the objective of today’s lab as well as the results of your experiment.
Objective: The objective of today’s lab was to observe using the method of
Results: We measured the experimental value of Series and Parallel to be 0.005 & 800 N/m.
The known value is 0.05 & 800 N/m . This gives a percent error/difference of 0%for our
experiment.
In a real lab usually, we get about 15-10% error percentage. If your calculated % difference
or % error values are zero think about if you use real springs what could be the sources of
error.
The deviation of our measurements from theory could be attributed to
Note - the following are never acceptable sources of error:
• “human error”
• rounding/calculation errors
• mysterious equipment malfunction
[Show More]












.png)






.png)