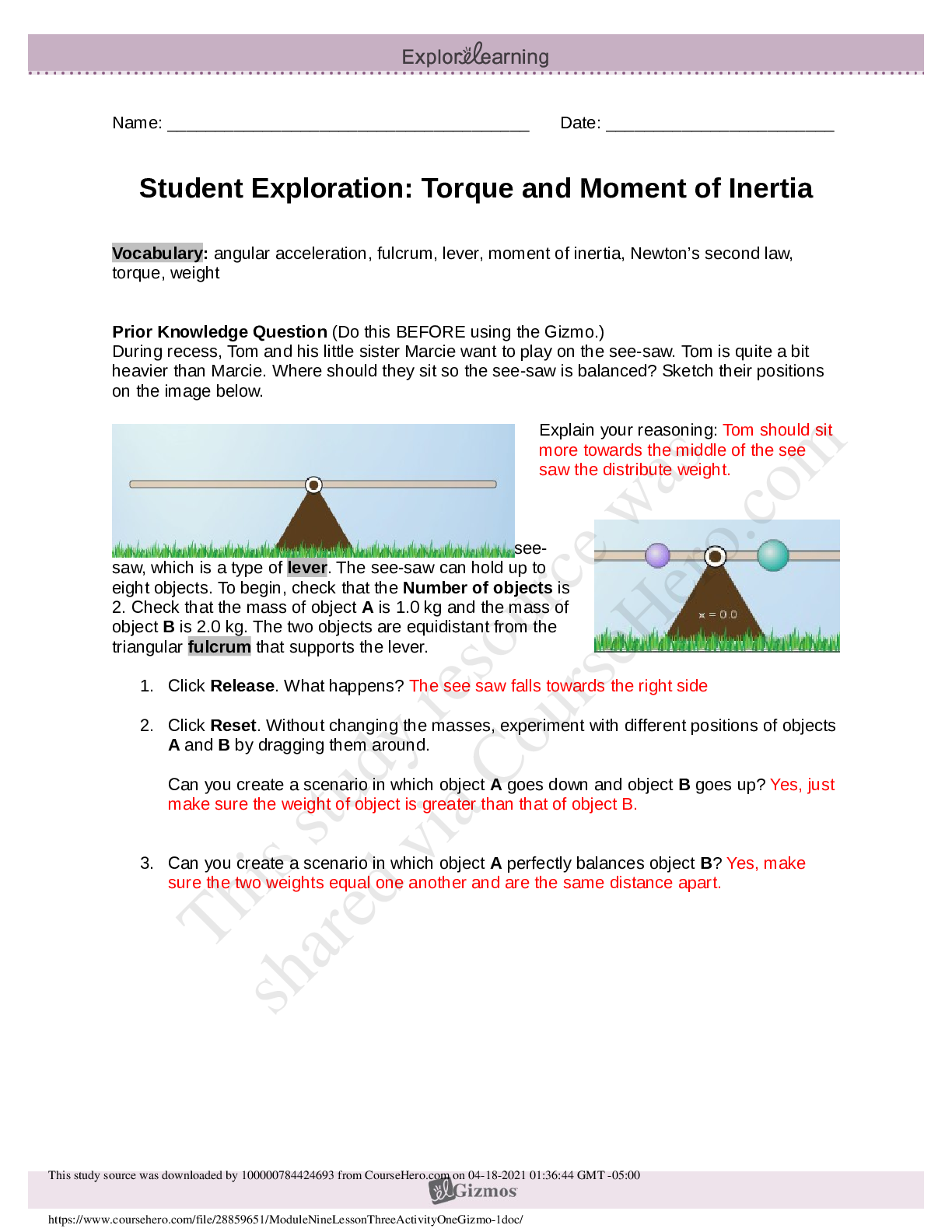
jung (dhj299) – #19 - Torque – fenton – (581) 1
This print-out should have 16 questions.
Multiple-choice questions may continue on
the next column or page – find all choices
before answering.
001 (part 1 of 2) 10.0
...
jung (dhj299) – #19 - Torque – fenton – (581) 1
This print-out should have 16 questions.
Multiple-choice questions may continue on
the next column or page – find all choices
before answering.
001 (part 1 of 2) 10.0 points
The arm of a crane at a construction site is
15.0 m long, and it makes an angle of 16.3
◦
with the horizontal. Assume that the maximum load the crane can handle is limited
by the amount of torque the load produces
around the base of the arm.
What maximum torque can the crane withstand if the maximum load the crane can
handle is 784 N?
Correct answer: 11287.3 N · m.
Explanation:
Let : d = 15.0 m and
Wmax = 784 N .
θ = 90.0
◦ − 16.3
◦ = 73.7
◦
, so
τmax = F d sin θ
= Wmax d sin θ
= (784 N)(15 m)(sin 73.7
◦
)
= 11287.3 N · m .
002 (part 2 of 2) 10.0 points
What is the maximum load for this crane at
an angle of 33.8
◦ with the horizontal?
Correct answer: 905.537 N.
Explanation:
Let : θ = 90.0
◦ − 33.8
◦ = 56.2
◦
We have the same maximum torque, so
W =
τmax
d sin θ
=
11287.3 N · m
(15 m) sin 56.2
◦
= 905.537 N .
003 10.0 points
A uniform horizontal rod of mass 1.4 kg and
length 0.6 m is free to pivot about one end
as shown. The moment of inertia of the rod
about an axis perpendicular to the rod and
through the center of mass is given by I =
m ℓ2
12
.
0.6 m
F 42
◦
pivot 1.4 kg
If a 9.9 N force at an angle of 42◦
to the horizontal acts on the rod as shown, what is the
magnitude of the resulting angular acceleration about the pivot point? The acceleration
of gravity is 9.8 m/s
2
.
Correct answer: 0.841454 rad/s
2
.
Explanation:
Let : ℓ = 0.6 m ,
m = 1.4 kg ,
θ = 42◦
, and
F = 9.9 N .
By the parallel axis theorem, the moment
of inertia of a stick pivoted at the end is
I = Icm + m d2
=
1
12
m ℓ2 + m
�
ℓ
2
�2
=
1
3
m ℓ2
.
The sum of the torques (counterclockwise rotation defined as positive) is
Xτ = F ℓ sin θ − m g
ℓ
2
= I α
[Show More]







.png)