Mathematics > QUESTIONS & ANSWERS > MAT 2355 Introduction to Geometry – THIRD ASSIGNMENT -University of Ottawa. (All)

MAT 2355 Introduction to Geometry – THIRD ASSIGNMENT -University of Ottawa.

Document Content and Description Below

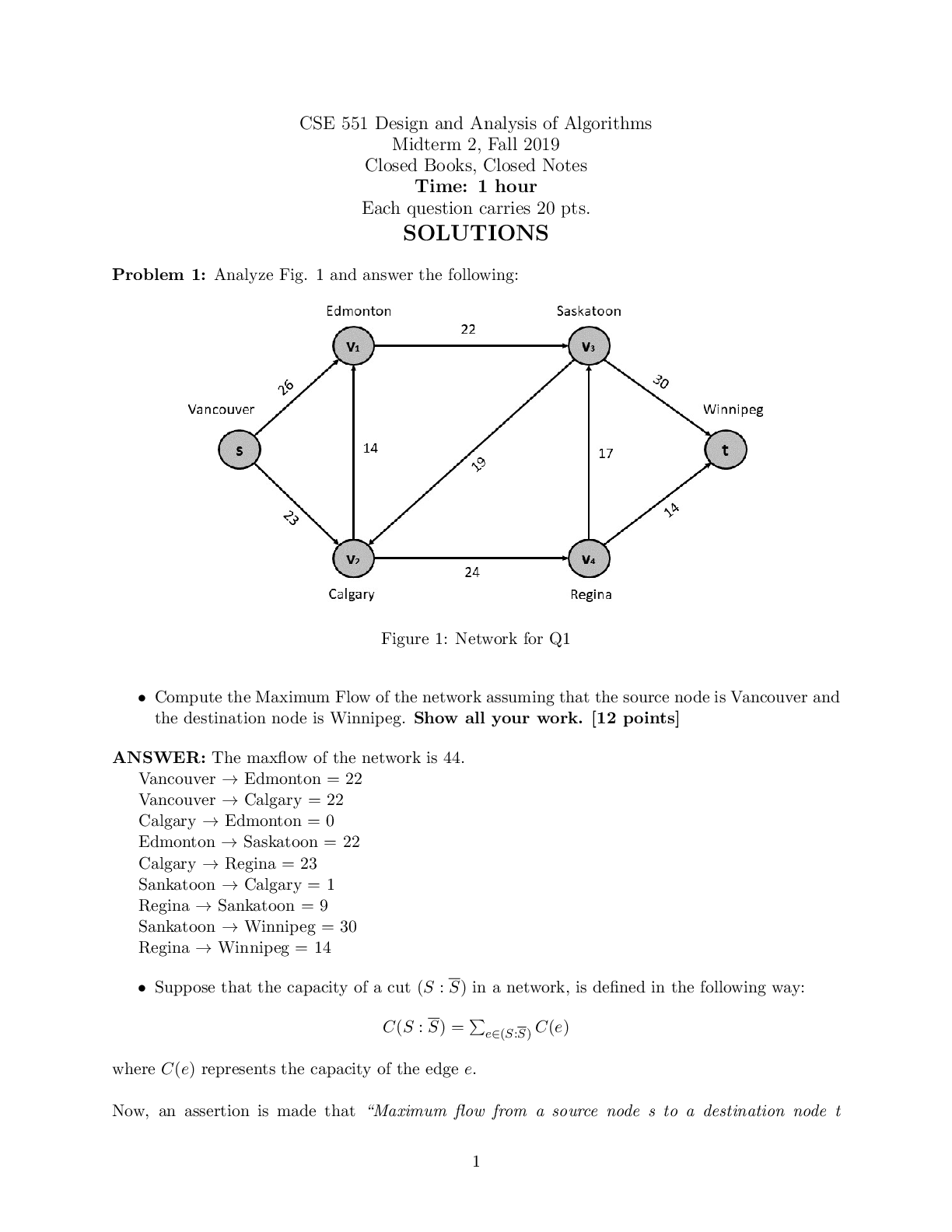
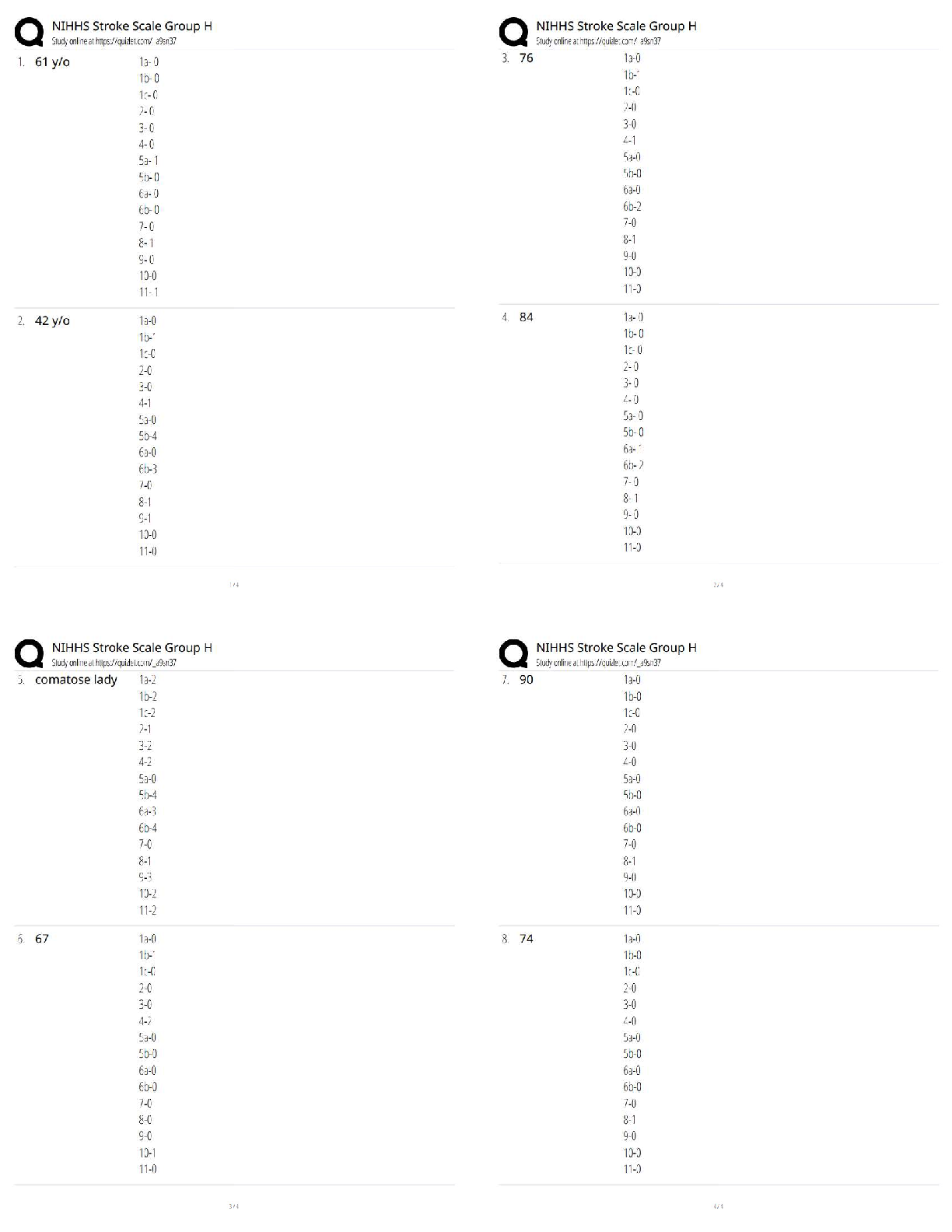
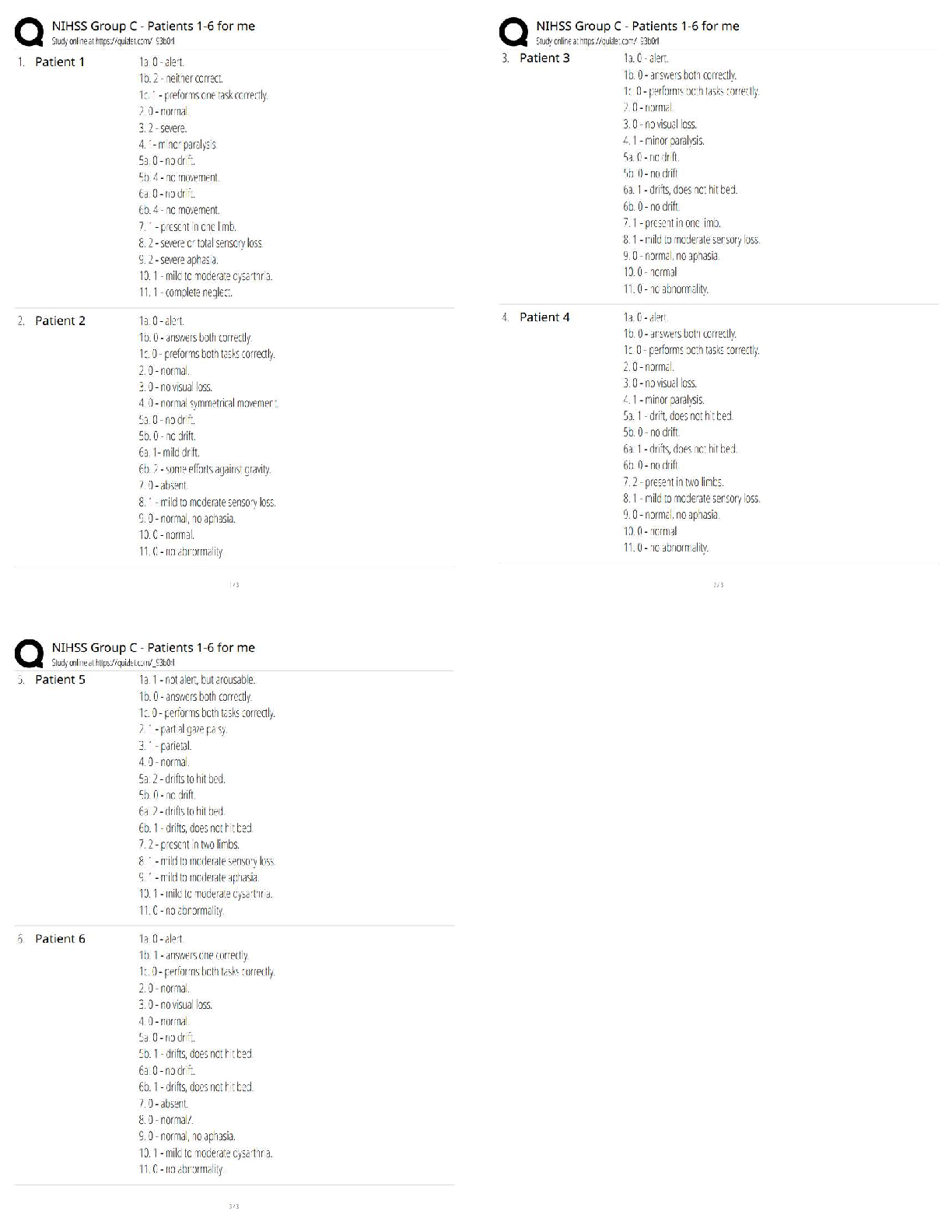
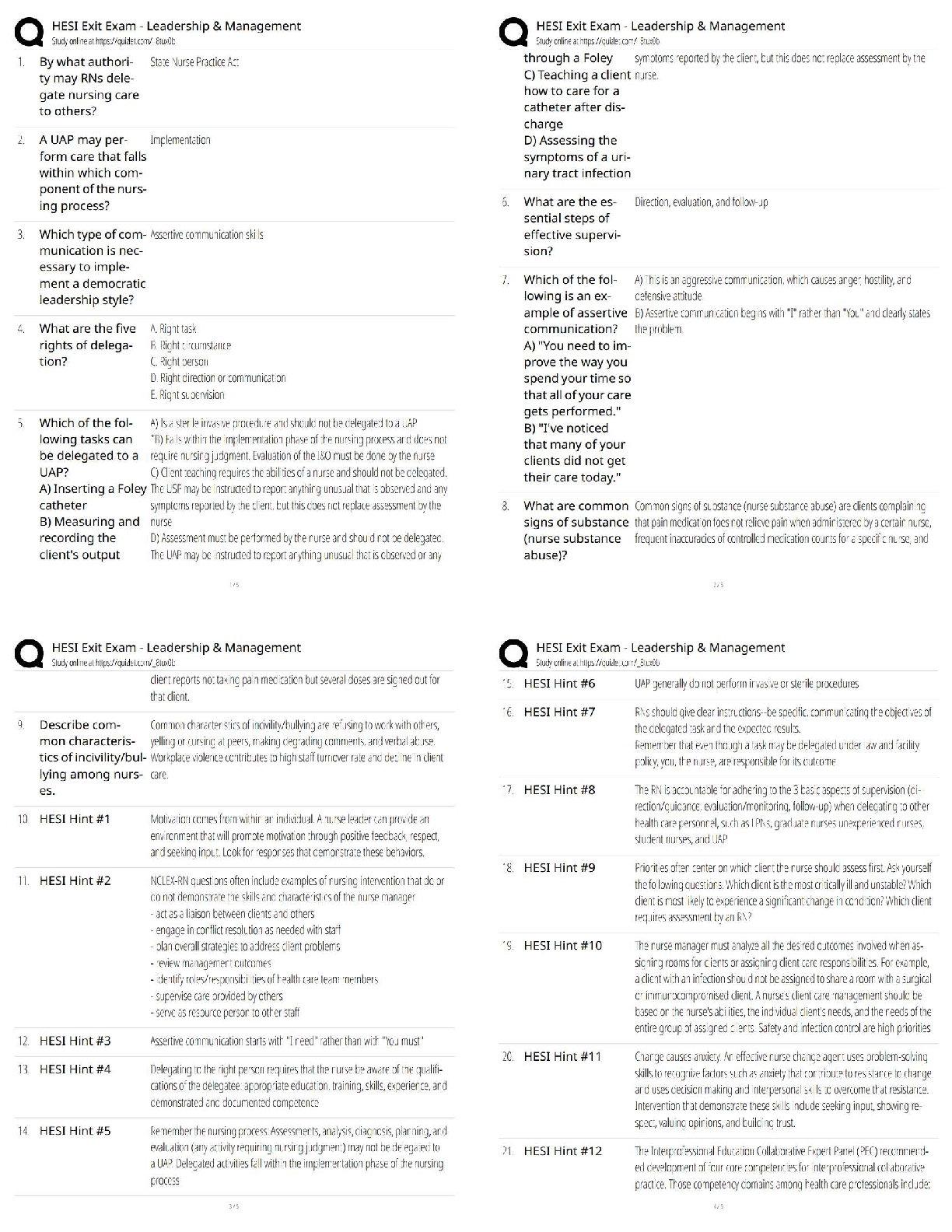
MAT 2355 Introduction to Geometry – THIRD ASSIGNMENT -University of Ottawa. MAT2355 – INTRODUCTION TO GEOMETRY – THIRD ASSIGNMENT QUESTION 1. In this question you should only write the fin ... al answers. Simplify your answers as much as possible. (a) [1 point] Compute the product of the following quaternion numbers: (-1 - i + 2k)(i - j) = 1 + i + 3j + k (b) [1 point] Let w = 1 - i + 2k. Then ... jwj = p1 + 1 + 4 = p6 and w-1 = 16 + 1 6i - 1 3k (c) [1 point] Let R : E3 ! E3 be the rotation in E3 with axis in the direction of the vector ~a = (-1; 2; -2) and angle θ = π 3 . If p 2 E3 denotes the point (0; 1; 0) then ... R(p) (d) [2 points] Let R : E2 ! E2 be the reflection such that R(0; 0) = (1; 1) and R(0; -1) = (2; 1). Then R is the reflection by the line y = mx + b where ... m = -1 and b = 1 Grading Scheme: (a): -.5 pts for each incorrect coefficient. (b): .5 +.5 (c): -.5 pts for each incorrect coefficient. (d): 1+1. QUESTION 2. For each of the following isometries determine if it is orientation-preserving or orientation-reversing. You do not need to justify your answer. 2 (a) [1 point] The map f : C ! C given by f(z) = iz - i + 2. (b) (b) [1 point] The composition of five reflections in E3. Grading Scheme: 1 + 1 3 QUESTION 3. [3 points] For each of the following statements, determine if the statement is true or false. Circle T for the true statements and F for the false statements. For each correct answer you will receive 1 point. For each incorrect answer you will receive -1 points. If you do not circle any of the letters next to a statement, you will receive 0 points for that statement. T F For every two line segments AB and A0B0 of equal length in E2, there exists a rotation R : E2 ! E2 such that R(A) = A0 and R(B) = B0. T F If the triangles 4ABC and 4A0B0C0 in E2 are similar (that is, \A = \A0, \B = \B0, and Grading Scheme: See the question statement. The minimum grade will be zero (i.e., if their total grade is negative, they receive zero. QUESTION 4. [2 points] A pentagon is a polygon with five sides (possibly with different lengths). Prove that for every pentagon ABCDE we have \A + \B + \C + \D + \E = 3π. 5 QUESTION 5. (a) [3 points] Using the method of Cartan–Dieudonne Theorem, write the isometry ´ f : C ! C ; f(z) = -iz + i - 1 as a product of three reflections. Determine the equations of the fixed lines of the three reflections. You should give the equations of these fixed lines in the form y = mx + b. (b) [1 point] Can f be written as a composition of fewer reflections? Justify your answer. 6 Q UESTION 6. [1 point] You are standing at a point A between two mirrors m1 and m2. You are looking at the reflection in m2 of your image in m1 (that is, point B in the picture). The mirrors suddenly start a counterclockwise rotation about their common axis (point O), but the angle between them does not change. What happens to the distance between you (point A) and your image (point B)? Does it increase? Decrease? Or does it remain fixed? Justify your answer. [Show More]

Last updated: 2 years ago

Preview 1 out of 6 pages

Buy Now

Instant download

We Accept: