Mathematics > QUESTION PAPER (QP) > CS 361 Computational Probability - University of Illinois_Homework 8. (All)

CS 361 Computational Probability - University of Illinois_Homework 8.

Document Content and Description Below

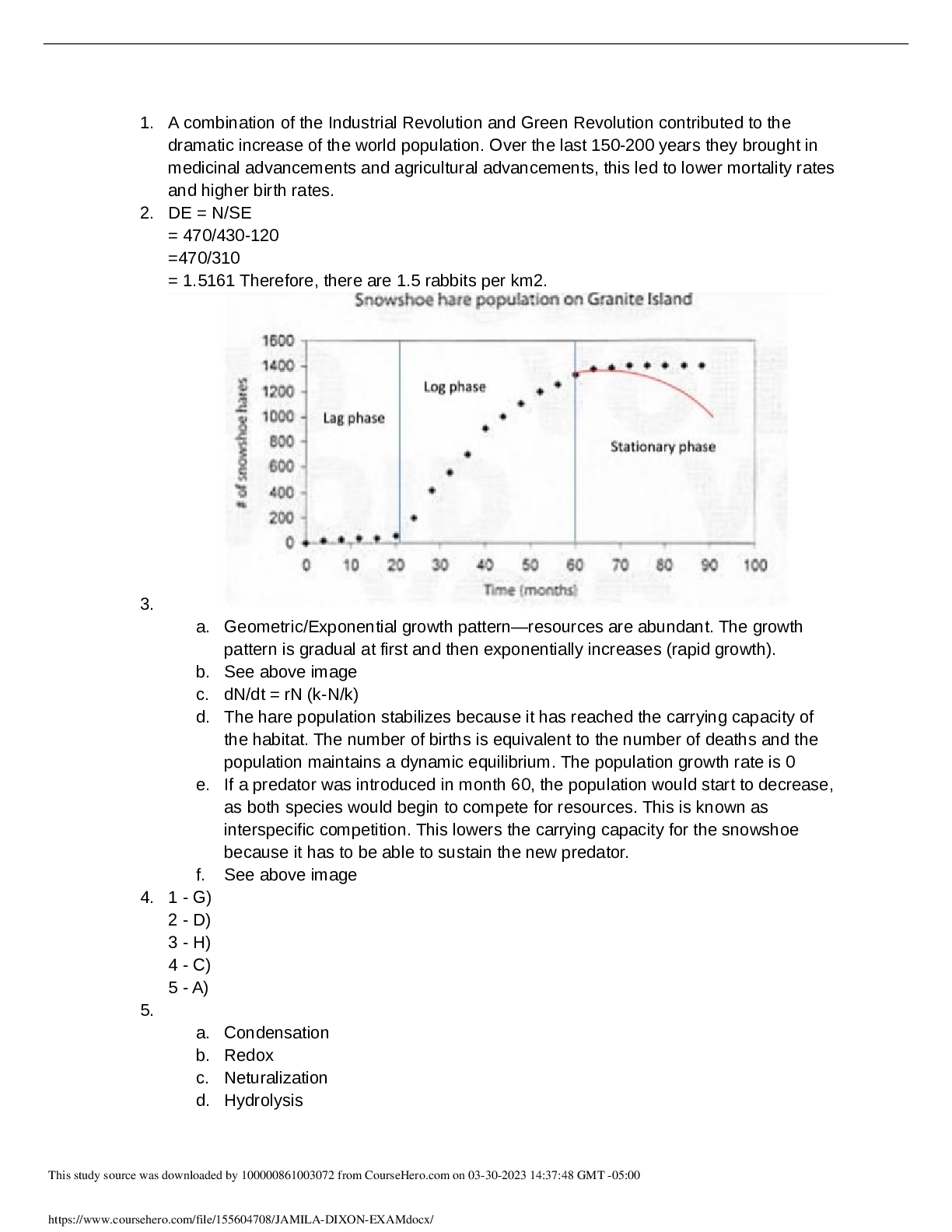
CS 361 Computational Probability - University of Illinois_Homework 8. Homework 8 1. We can write out the likelihood function for the exponential distribution as L(θ) = P(xjθ) = θe-θx If we ass ... ume that all the values in the set are found independently we can write the likelihood function as follows: NY X2i θe-θxi Next we can take the log of both sides to yield: ln(L(θ)) = ln( NY X2i θe-θxi) = NX X2xi ln(θexp(-θxi)) = NX X2xi ln(θ) + ln(exp(-θxi) = NX X2xi ln(θ) - θxi We can take the log of theta term and factor it out of the summation along with the theta constant multiplied by x to get: Ln(L(θ)) = Nln(θ) - θ NX X2xi xi We can differentiate both sides to give: d dθln(L(θ)) = dθ d Nln(θ) - dθ d θ XN X2xi xi = N θ - NX X2xi xi Setting this equal to 0 and solving for theta gives: θ^ = N PN X2xi xi 1 2. The maximum likelihood function for a Poisson distribution is: L(λ) = N1 PN i=1 Xi Since the max likelihood function is the average of the number of observations in a given period of time we can calculate he average number of popup windows for each day separately. (a)i. For day 1: (3 + 1 + 4 + 2) ∗ 14 = 2:5 counts/hr ii. For day 2: (2 + 1 + 2) ∗ 1 3 ≈ 1:667 counts/hr iii. For day 3: (3 + 2 + 2 + 1 + 4) ∗ 1 5 = 2:4 counts/hr (b) Since for day 4, the observer already summed the number of observations and we have the given time we can just divide the sum by the period of time they were recording observations for to get: 13 6 ≈ 2:167 counts/hr (c) The MLE for the intensity for all the days taken together is just the sum of all the occurrences divided by the total time spend browsing: (3+1+4+2+2+1+2+3+2+2+1+4+13)∗ 4+3+5+6 1 ≈ 2:22 [Show More]

Last updated: 2 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: