Mathematics > QUESTIONS & ANSWERS > Pennsylvania State University MATH 141 CALC ANLY GEOM II . n-Class Worksheet Week 5. Solurions. Win (All)

Pennsylvania State University MATH 141 CALC ANLY GEOM II . n-Class Worksheet Week 5. Solurions. Winter 2023.

Document Content and Description Below

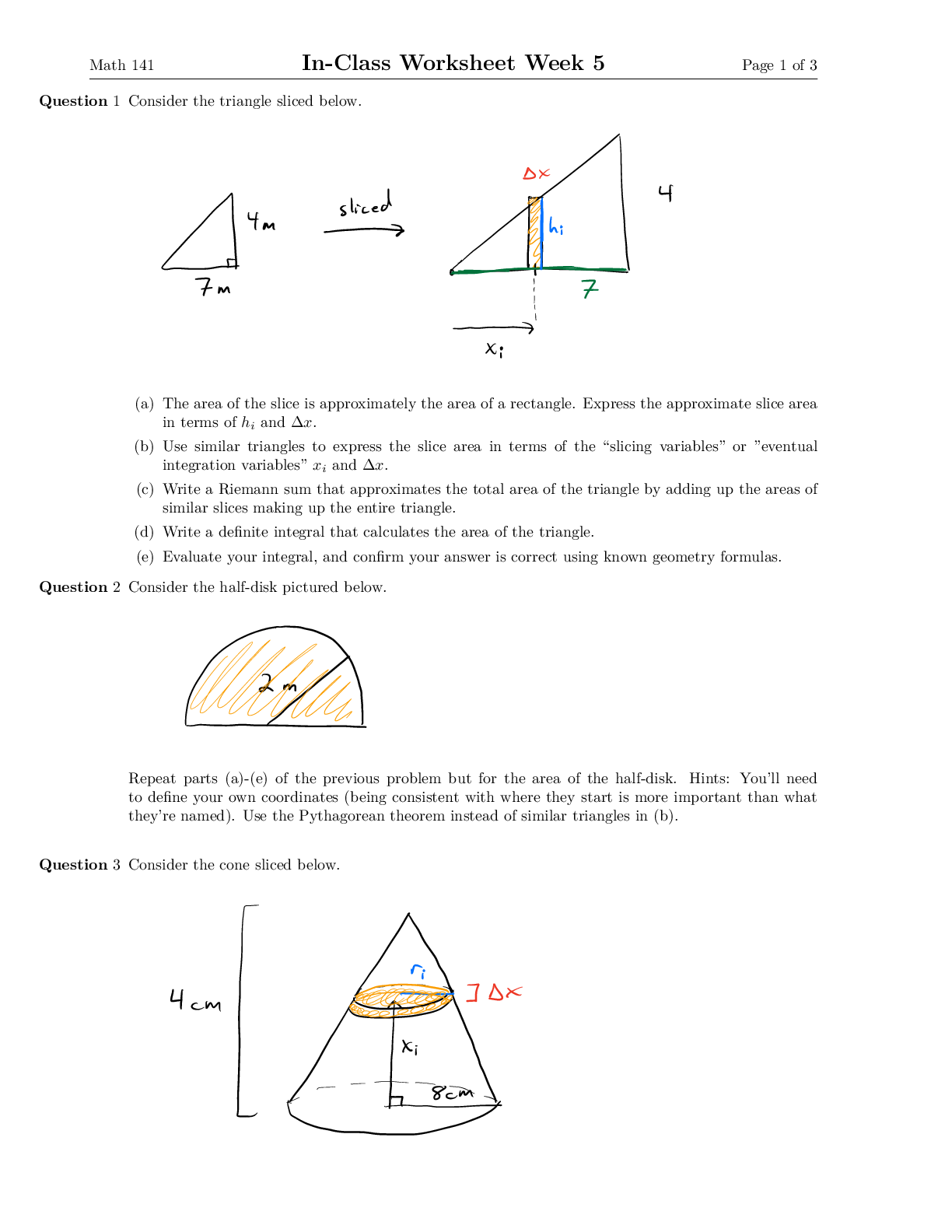
Math 141 In-Class Worksheet Week 5 Page 1 of 3 Question 1 Consider the triangle sliced below. (a) The area of the slice is approximately the area of a rectangle. Express the approximate slice area i ... n terms of hi and ∆x. (b) Use similar triangles to express the slice area in terms of the “slicing variables” or ”eventual integration variables” xi and ∆x. (c) Write a Riemann sum that approximates the total area of the triangle by adding up the areas of similar slices making up the entire triangle. (d) Write a definite integral that calculates the area of the triangle. (e) Evaluate your integral, and confirm your answer is correct using known geometry formulas. Question 2 Consider the half-disk pictured below. t.gg Repeat parts (a)-(e) of the previous problem but for the area of the half-disk. Hints: You’ll need to define your own coordinates (being consistent with where they start is more important than what they’re named). Use the Pythagorean theorem instead of similar triangles in (b). Question 3 Consider the cone sliced below. (a) The volume of the slice is approximately the volume of a cylinder. Express the slice volume in terms of ri and ∆x. (b) Use similar triangles to express the slice volume in terms of the “slicing variables” or ”eventual integration variables” xi and ∆x. (c) Write a Riemann sum that approximates the total volume of the cone by adding up the volumes of similar slices making up the entire cone. (d) Write a definite integral that calculates the volume of the cone. (e) Evaluate your integral, and confirm your answer is correct using known geometry formulas. (f) Suppose that the cone is made of sand with variable density. The density of the sand is given by ρ(x) = 8 - x2 4 g cm3 (meaning the sand closer to the floor is more tightly packed), where x is the distance to the floor. Approximate the mass of the pictured slice in terms of xi and ∆x. (g) Write a definite integral that calculates the total mass of the cone. Question 4 Consider the square-based pyramid pictured below. Repeat parts (a)-(d), (f), (g) of the previous problem but for the volume and mass of the pyramid. Use the same density function, with x still being the distance to the floor. Hint: Your slice will NOT be approximately cylindrical this time, so you’ll need to make some adjustments. Question 5 Consider the region bounded by y = x4, y = 16 and the y-axis. (a) Find the area of the region. (b) Write, but do not evaluate, an integral to find the volume of the solid obtained by rotating the region about the x-axis. (c) Write, but do not evaluate, an integral to find the volume of the solid obtained by rotating the region about the y-axis. (d) Write, but do not evaluate, an integral to find the volume of the solid whose base is the region and whose cross sections perpendicular to the x-axis are squares. (e) Write, but do not evaluate, an integral to find the volume of the solid whose base is the region and whose cross sections perpendicular to the y-axis are equilateral triangles. Question 6 Integral Grab Bag! [Show More]

Last updated: 2 years ago

Preview 1 out of 3 pages

Buy Now

Instant download

We Accept: