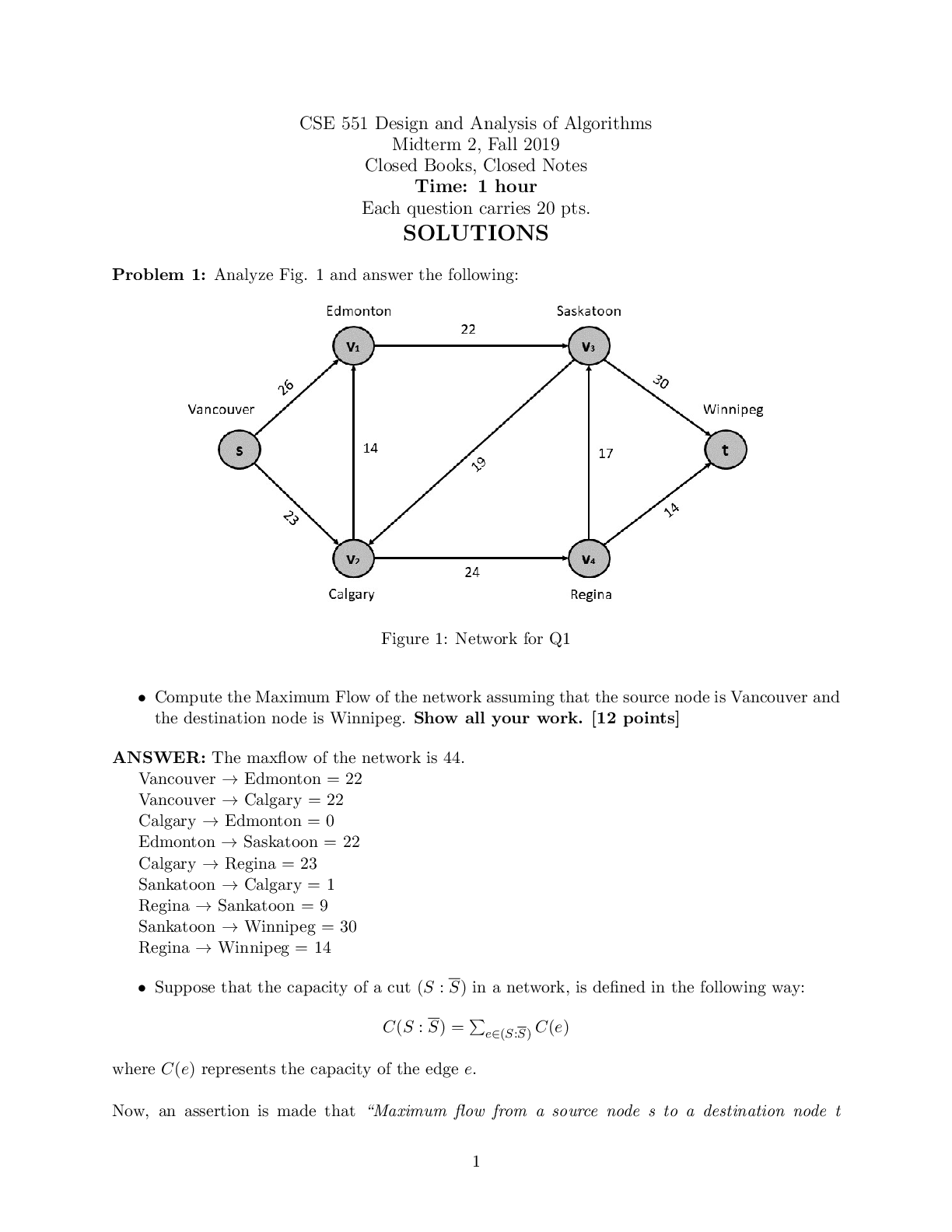
eBook Business Statistics Abridged, Australia and New Zealand, 8th Edition By Eliyatham Selvanathan, Saroja Selvanathan, Keller
$ 25

Liberty University - ETHICS 205 Test 24 Latest Study Guide (Latest 2021) 100% Correct Study Guide, Download to Score A