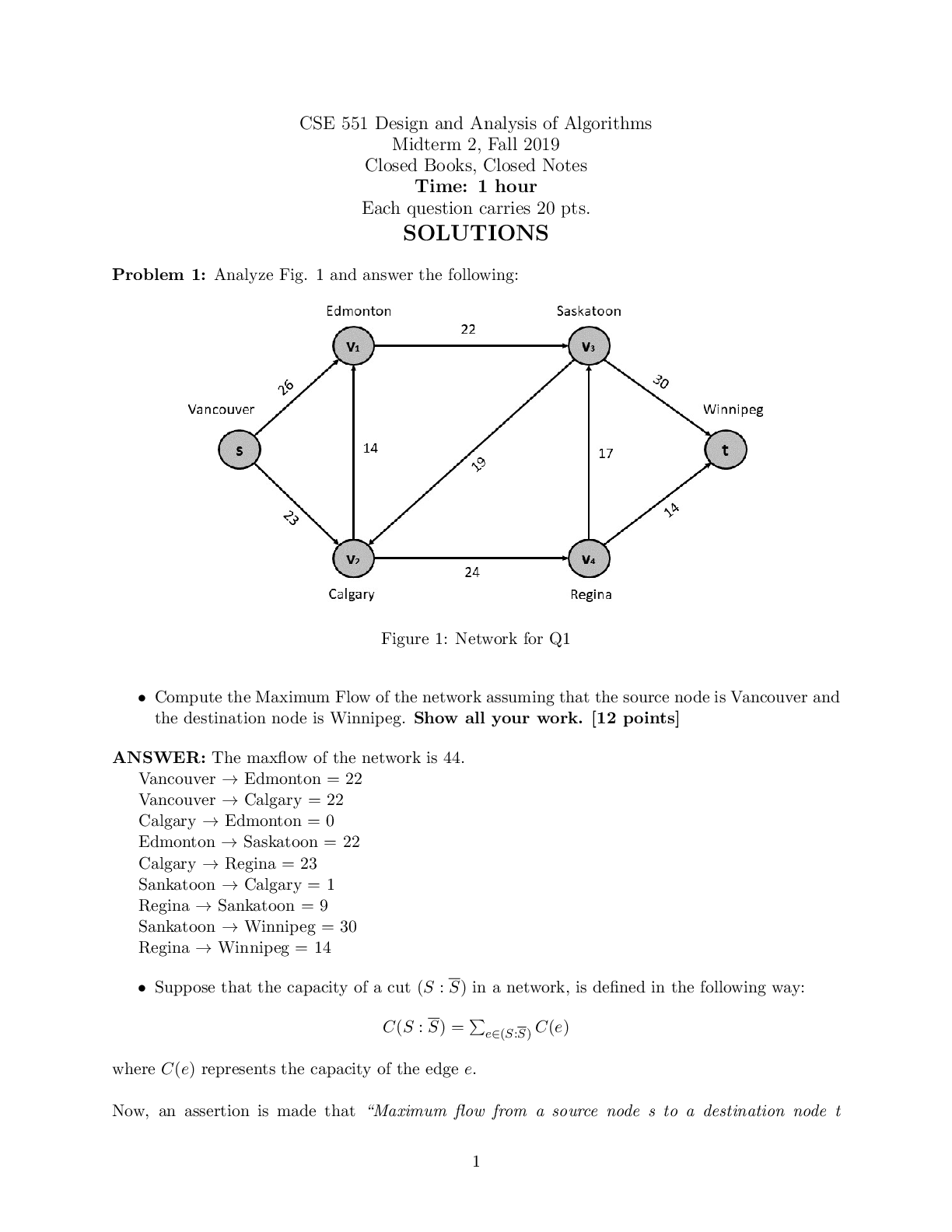
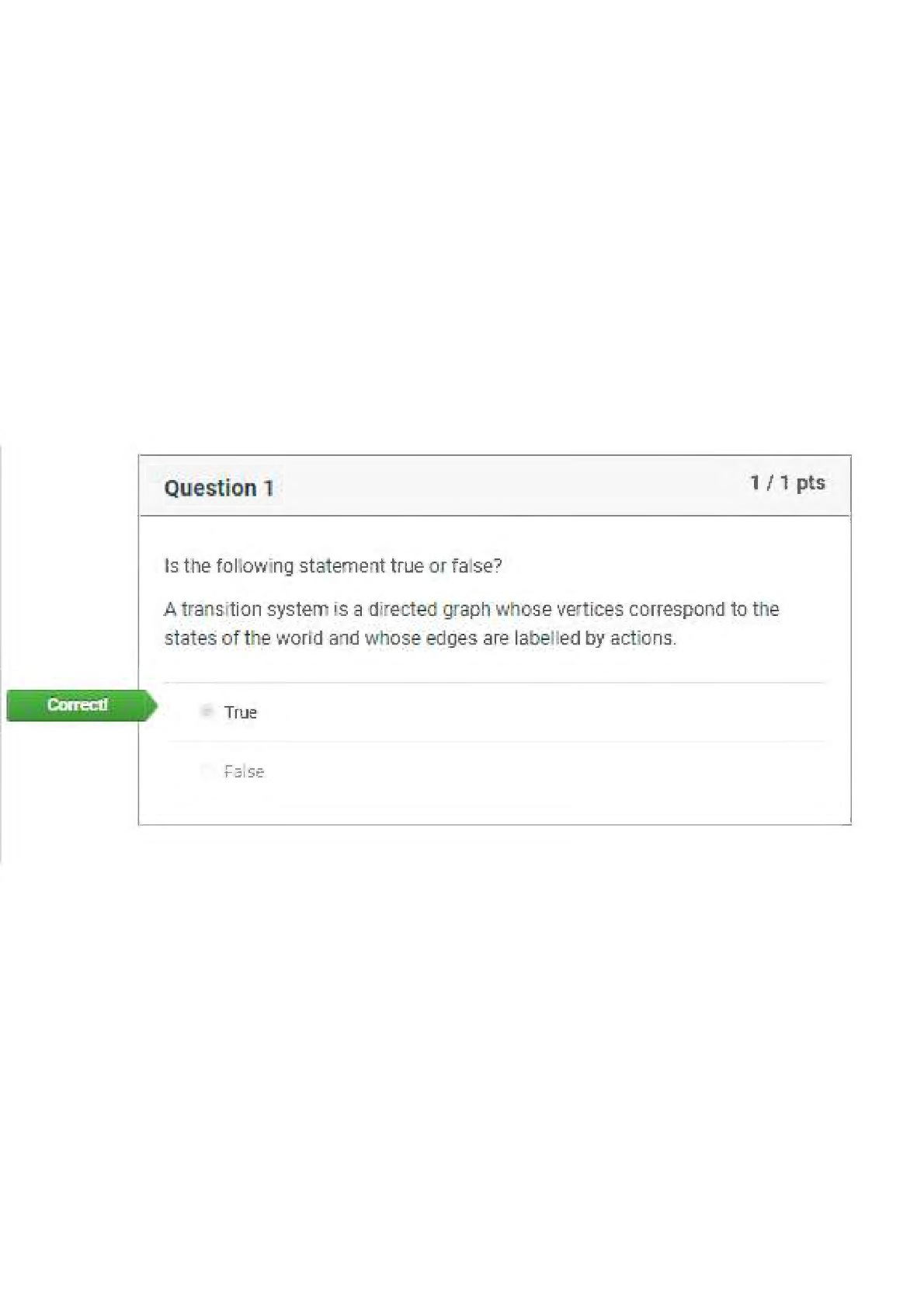
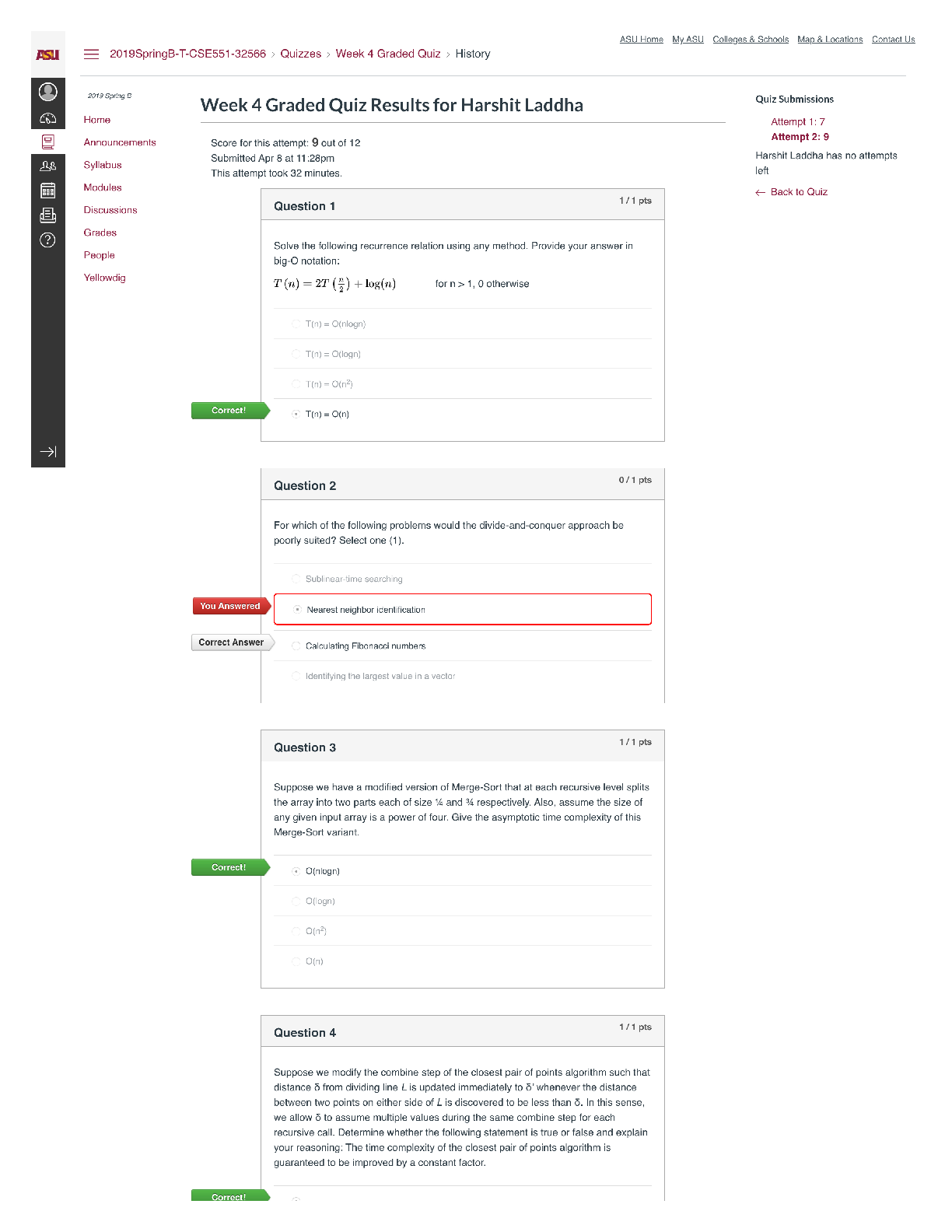
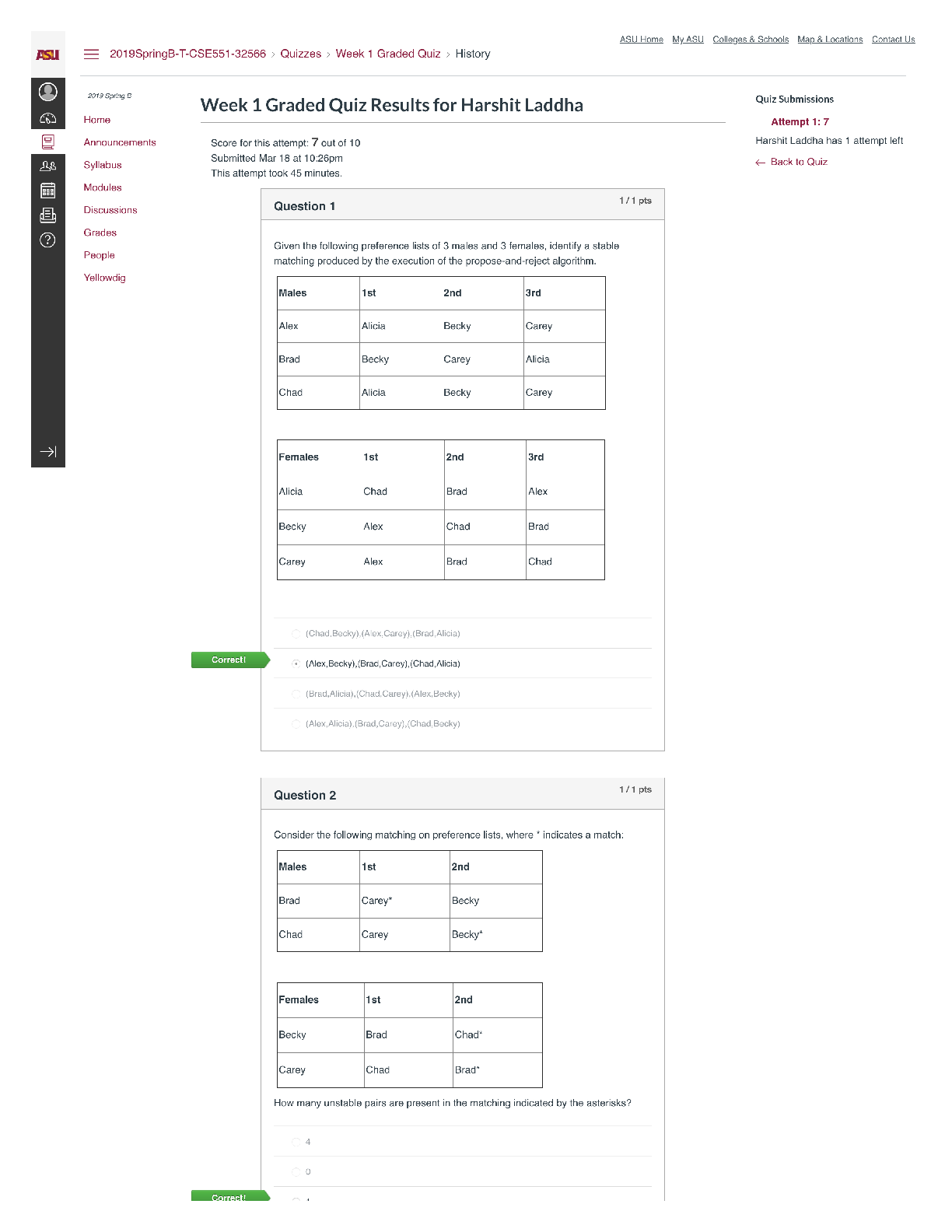
SEC 572 Week 8 Final Exam | Latest complete solution.
$ 9.5
.png)
Individual Assignment part B (5% of final grade)
$ 7

DoD Government Purchase Card Refresher Training | All Answers are Correct
$ 5
.png)
AQA GCSE MATHEMATICS 8300/3F Foundation Tier Paper 3 Calculator Mark scheme June 2021 Version: 1.0 Final
$ 10
ECE-GY 6483 Midterm 2 Submission | New York University. UPDATED
$ 8

Child Psychology A Canadian Perspective, 3e Alastair Younger, Scott Adler, Ross Vasta (Solution Manual)