MHF4U_Dragon's Den Mid-Unit Assignment Colegio San Bartolomé la Merced MATH CALCULUS. Q&A. 100%

Document Content and Description Below

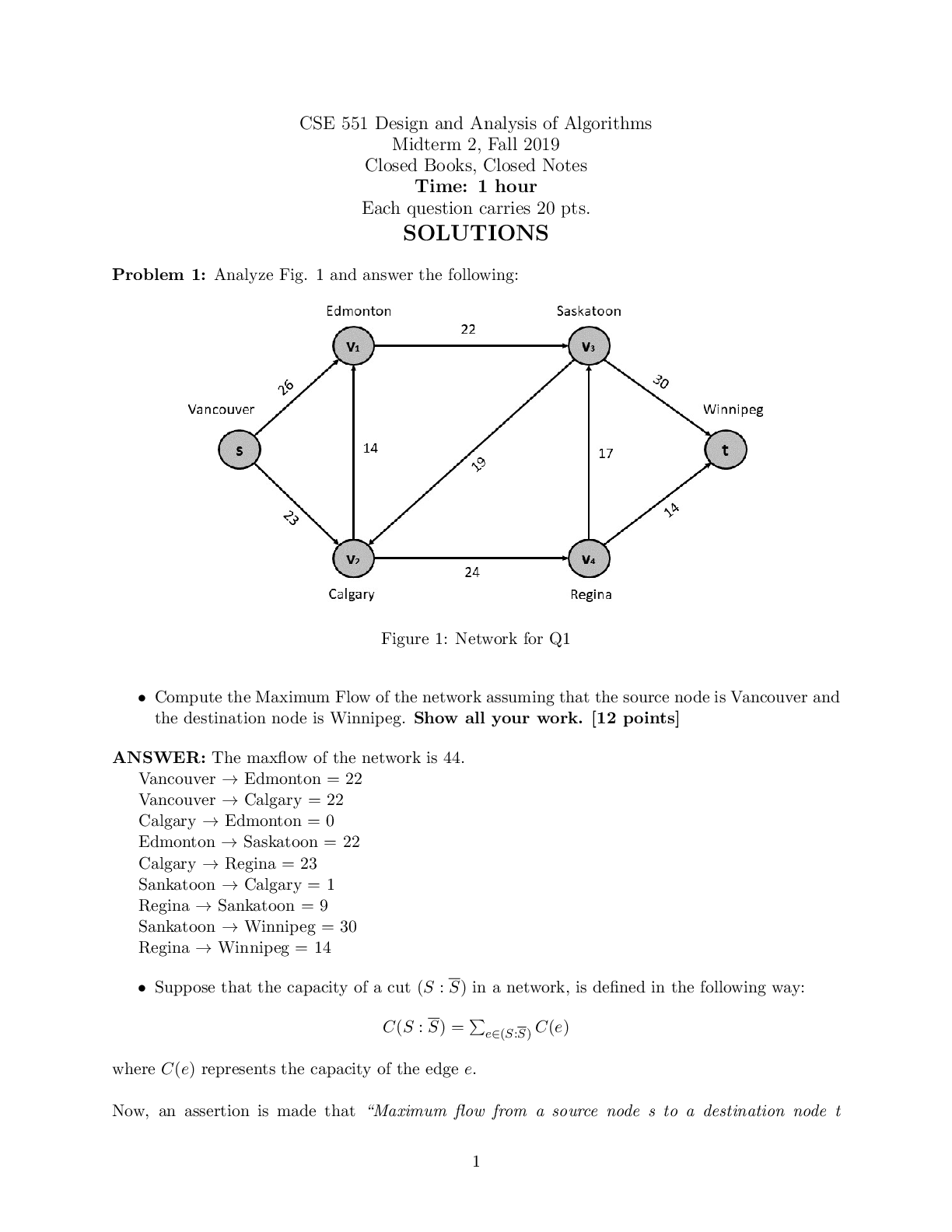
Dragon's Den Mid-Unit Assignment Santiago Poveda Henao, MHF4U m1+Pitch Hello dragons, my name is Santiago Poveda, I am from Colombia and I want to present you with a product, I came here to ask f ... or $50 000 for 20% of the company, my product is a 5-blade scissors that specializes in chopping and cutting any type of fruits and vegetables. Its modernized design makes it durable and useful at the same time, essential for all kitchens. Disclaimer: The product used for this activity was not created by me, but is instead a real product distributed by the Universal company in ColombiaCosts To make this magnificent product we need stainless steel sheets, it is sold for $2 per kilogram , the scissors weight 179 grams so it costs around $0.36 to manufacture one pair of scissors. This leaves us with a function of C(x) = 0.36x for the costs of production for the product, where x is the number of units produced and C(x) is the total costs.Price increments To obtain the highest revenue possible we are going to put the price at $5 and use the average monthly sales of 500 units to get our function, it's important to take into account that every $0.15 we would like to increase the price of the item, it would decrease the sold units by 10, with this information we can establish two functions based on the number of price increments we would want to do, the price per unit and the number of sold items. P(x) = 0.15x + 5 N(x) = 500 - 10x Where x is the number of price increments of the productRevenue function With this way we can obtain a revenue function based on the amount of price increments we want to make: R(x) = (number of products sold) x (price) R(x) = (500 - 10x) x (0.15x + 5) R(x) = 75x + 2500 - 1.5x2 - 50x R(x) = -1.5x2 + 25x +2500 This will give us the following graphRevenue graph As you can see in the graph we have a clear maximum point at (8,2604), this is the amount of price increments we need to make to obtain the highest amount of revenue. If you can see on the graph and when you solve for x algebraically you obtain both points where the revenue will be 0, from increasing to much the price, meaning less sales and from decreasing too much the price, despite the increasing salesHighest Revenue Since the highest revenue achievable is with the increasing the price 8 times by $0.15, that means that the best price for our product is $6.2, leaving us with a final revenue function of: R(x) = (number of sold products) x (new selling price) R(x) = 6.2x where x is the number of products sold. Now to show you the overall profit from this product we need to rest the costs of production from the revenue to get the total gains. P(x) = R(x) - C(x) P(x) = 6.2x - 0.36x P(x) = 5.84x , where x is the number of products sold and P(x) is the profitProfit As you can see from the graph the profit from this product increases arithmetically and these are just the profits monthly, through the years the money accumulates and with the increasing market for this product, the gained money will be even higherRealistic? I am actually not sure if my results are realistic, I would say that the functions worked seem possible in real lifebut they dont take into account all the variables in making a product, I learned that even when the process is simplified, selling products can be complicated, we didn’t get to commercialization, time of production and other components, so that made me realize how complex this topic is. I would say that the hardest part was thinking of an idea or product and then searching for the materials and prices, that took a while because the materials for my product varied greatly from each provider so that choice was a bit hard. [Show More]

Last updated: 2 years ago

Preview 1 out of 9 pages