Mathematics > QUESTIONS & ANSWERS > Questions and Answers > Memorial University of Newfoundland - ENGI 9116ENGI 9116 - Assignment 2 solu (All)

Questions and Answers > Memorial University of Newfoundland - ENGI 9116ENGI 9116 - Assignment 2 solution - W2020

Document Content and Description Below

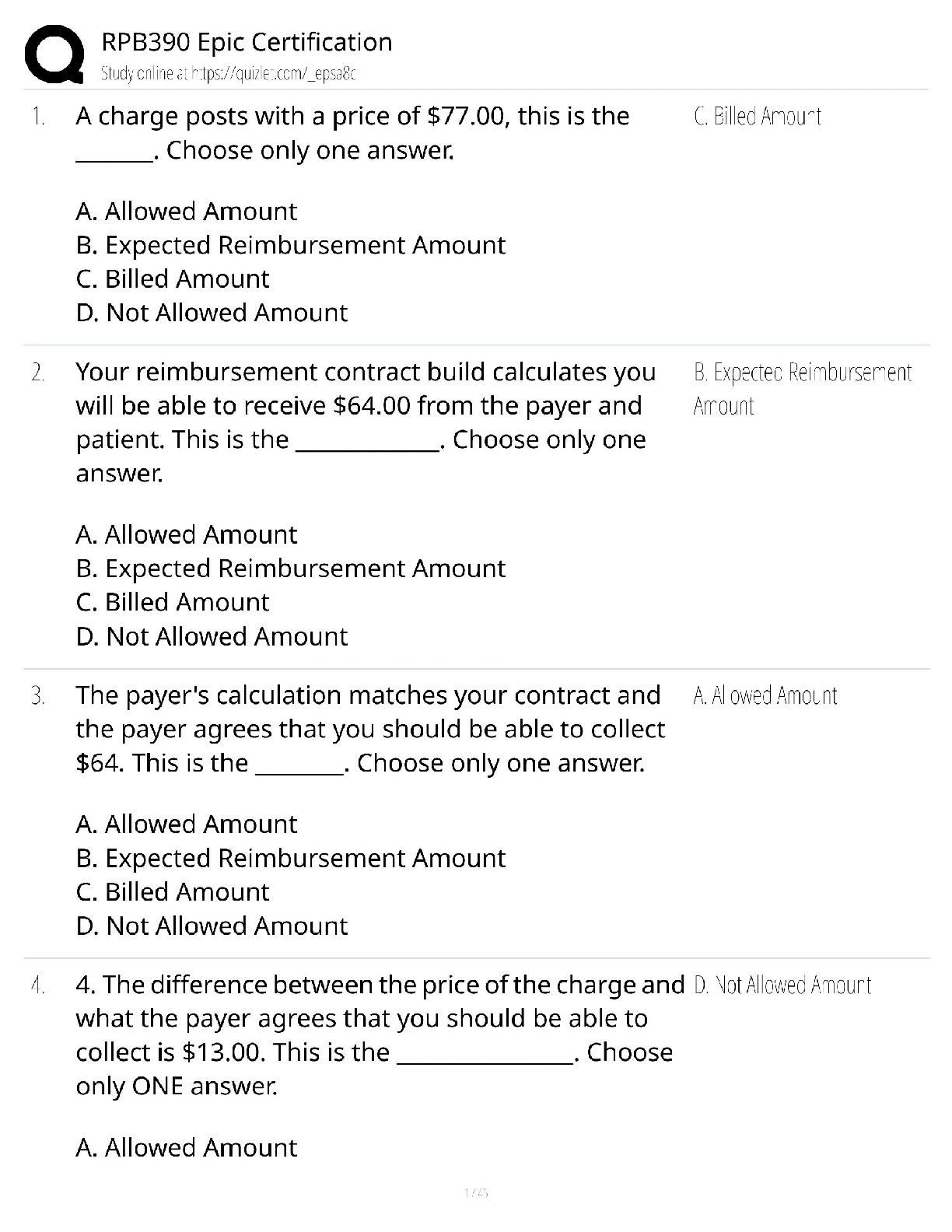
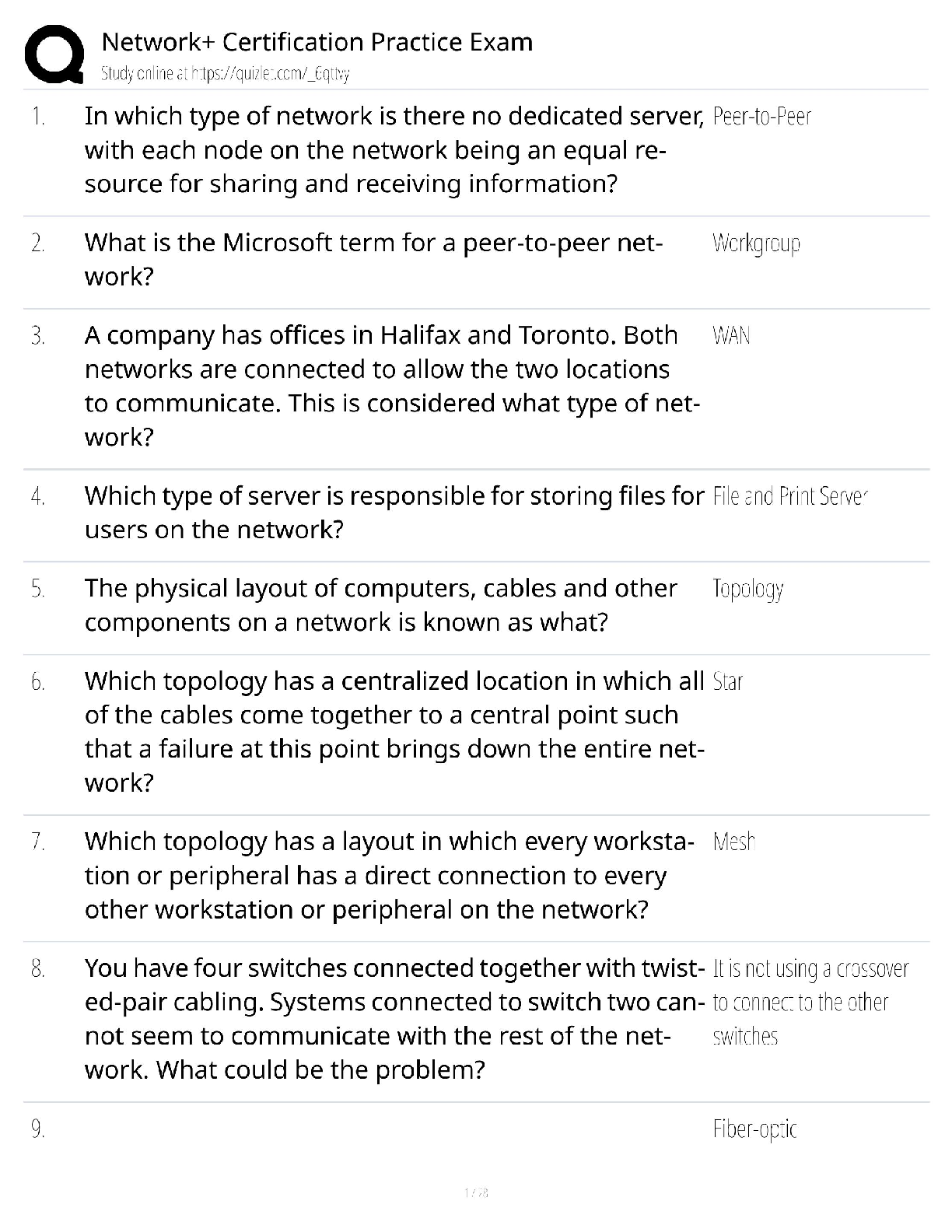
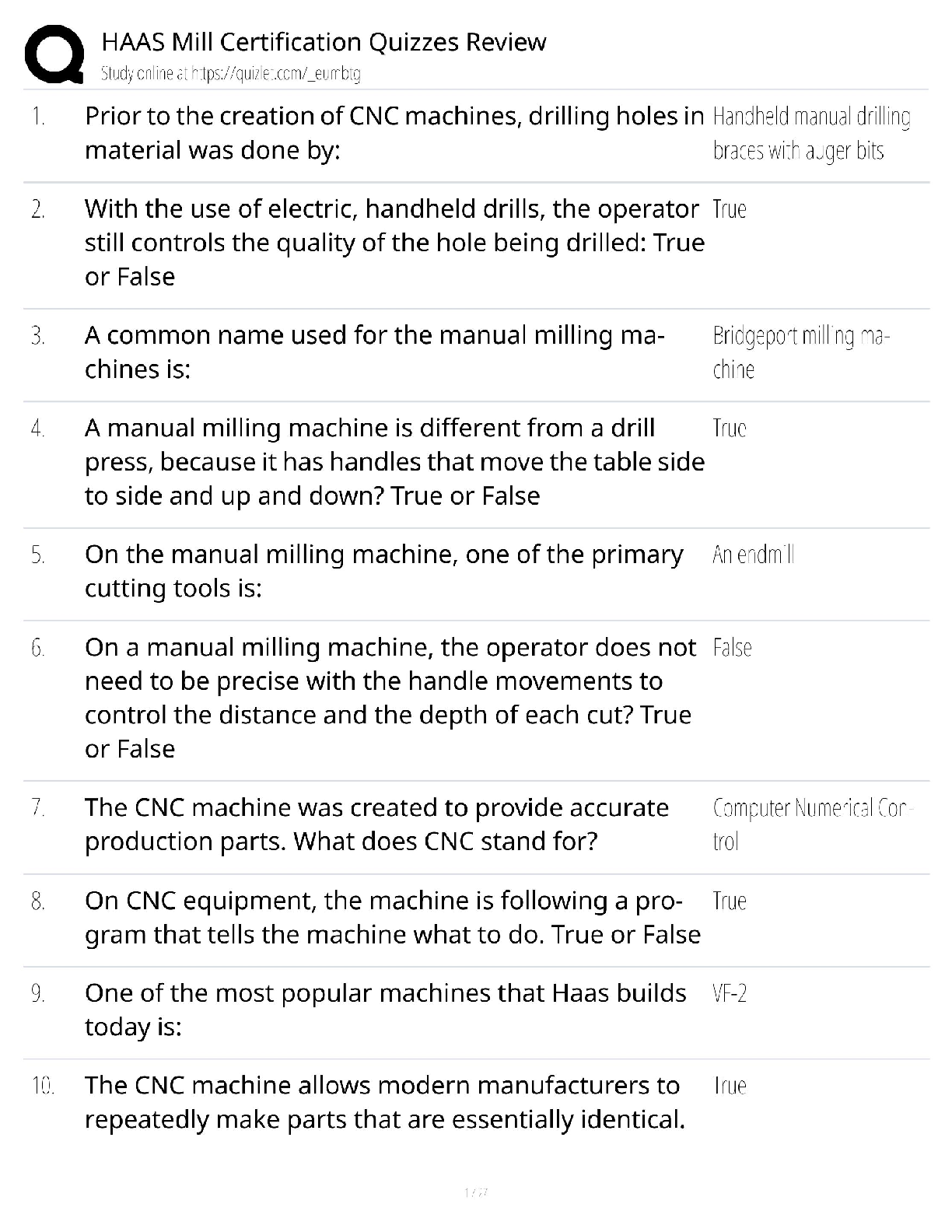
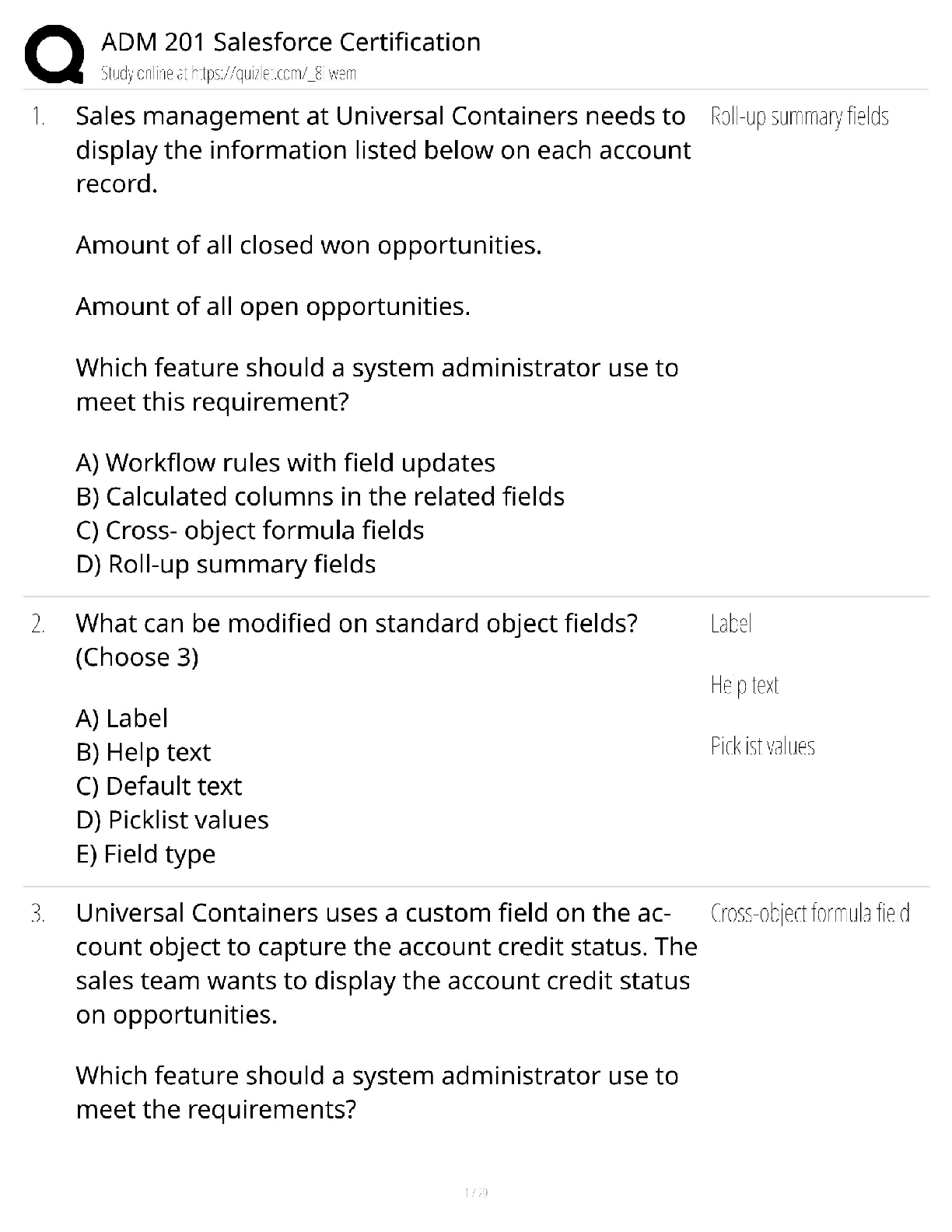
Advanced Reliability Engineering (ENGI 9116) Solution for Assignment 2 - W 2020 1. Number of identical and critical components, ? = 30 Design life, ??= 15 ????? For a system constant failure ra ... te model R(??) = ?-?????? R(10) = ?-????15 = 0.98 System failure rate: System failure rate where n = 30 independent, identical and critical components, λ?= component failure rate, ???��?= - (ln 0.5) ∗ 2. The system is a Poisson process Where ??(?) is the probability mass function; λt = mean or expected number of failures over time ?; ?is the number of failures. System reliability, Thus, the custodian must maintain 2 spare tubes. 3. Idle time, ??= 16 ℎ????; Operating time, ??= 8 ℎ????; Failure on demand: p = 1 120 Failure rate while in operation: λ?= 1 1050 Failure rate while idle: Design life, ?? R(??) = ?-λ?????= 0.95 4. Given that: The reliability for one component For the system, the reliability for a design life of 1 year will be ? ???= 1 - (1 - ?1)?= 1 - (1 - ?-(?? )?)?= 1 So, the maximum number is calculated (parallel) as 4 As we know for median time to failure the system reliability is half. Therefore, substituting the values of Weibull distribution parameters, we get By hit and trail method, LHS should be equal to RHS of above equation LHS tmedian Therefore, median time to failure is 1.59 yrs. Comparing with a Weibull distribution Thus, failure distribution of motor B is: F(t) = 1 - R = 1 - ?-(1∗10 ? 5)2 rs (5%) Therefore, Motor A is preferred due to its higher MTTF. Therefore, Motor B is preferred due to its higher reliability d. The conditional reliability of functioning for additional 9 years given that it had for the first Therefore, the replacement cost of Motor B would be preferably reduced due to its higher reliability. d. (i) Expected value of having the first-year warranty is the risk of losing the value of the VCR, quantified as $500 (4%) Expected value = Probability of failure * Consequence (value of VCR) Since the expected value is less than the cost of warranty for the first year, the first-year warranty should not be purchased (ii) Expected value of having the second-year warranty Since the expected value of the second year is greater than the cost of the warranty, the secondyear warranty should be purchased. e. Probability of failure for t = 2years (4%) Total cost of warranty = $25 + $40 = $65 Expected value for the total cost of warranty Therefore, both warranties should not be purchased as the expected value is less than the total cost. [Show More]

Last updated: 3 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: