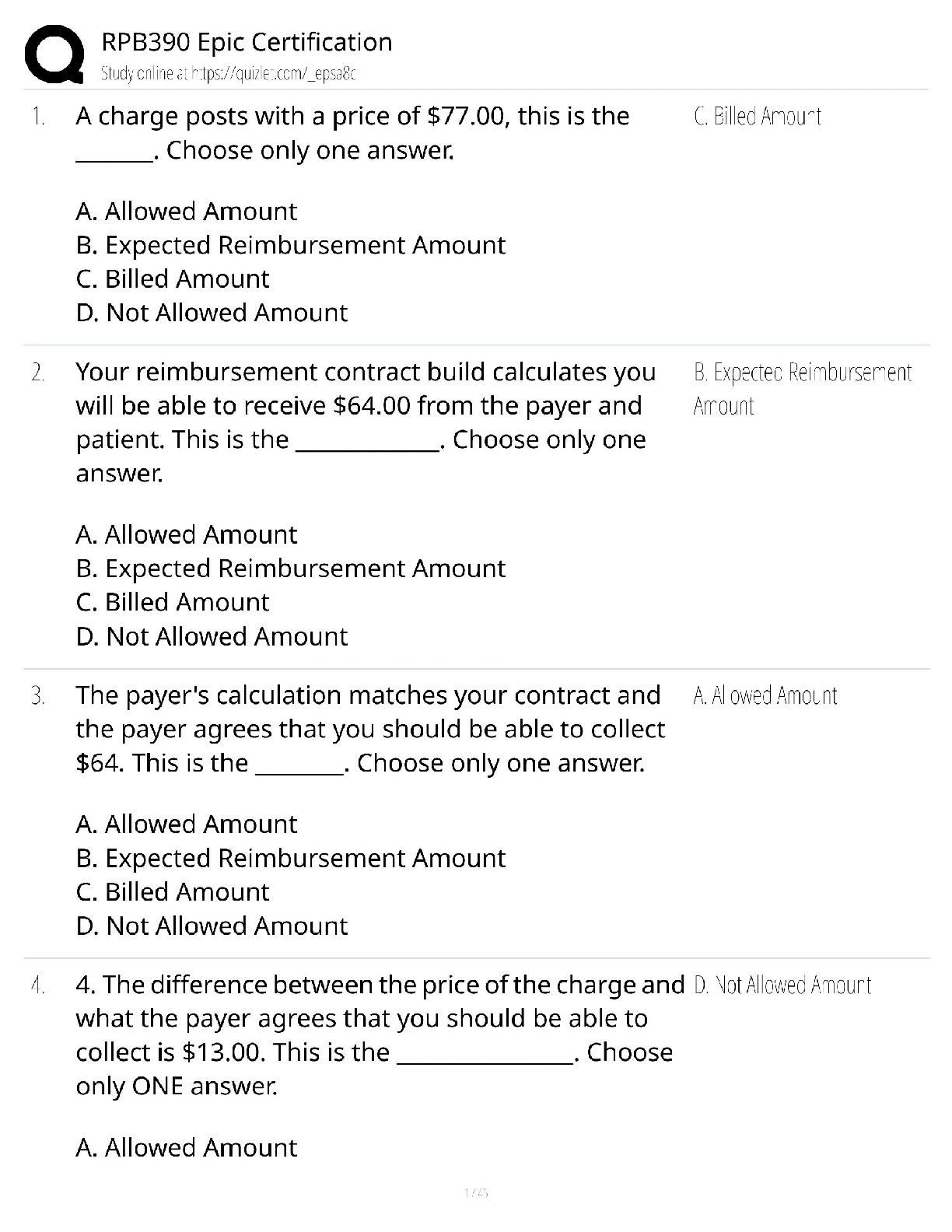
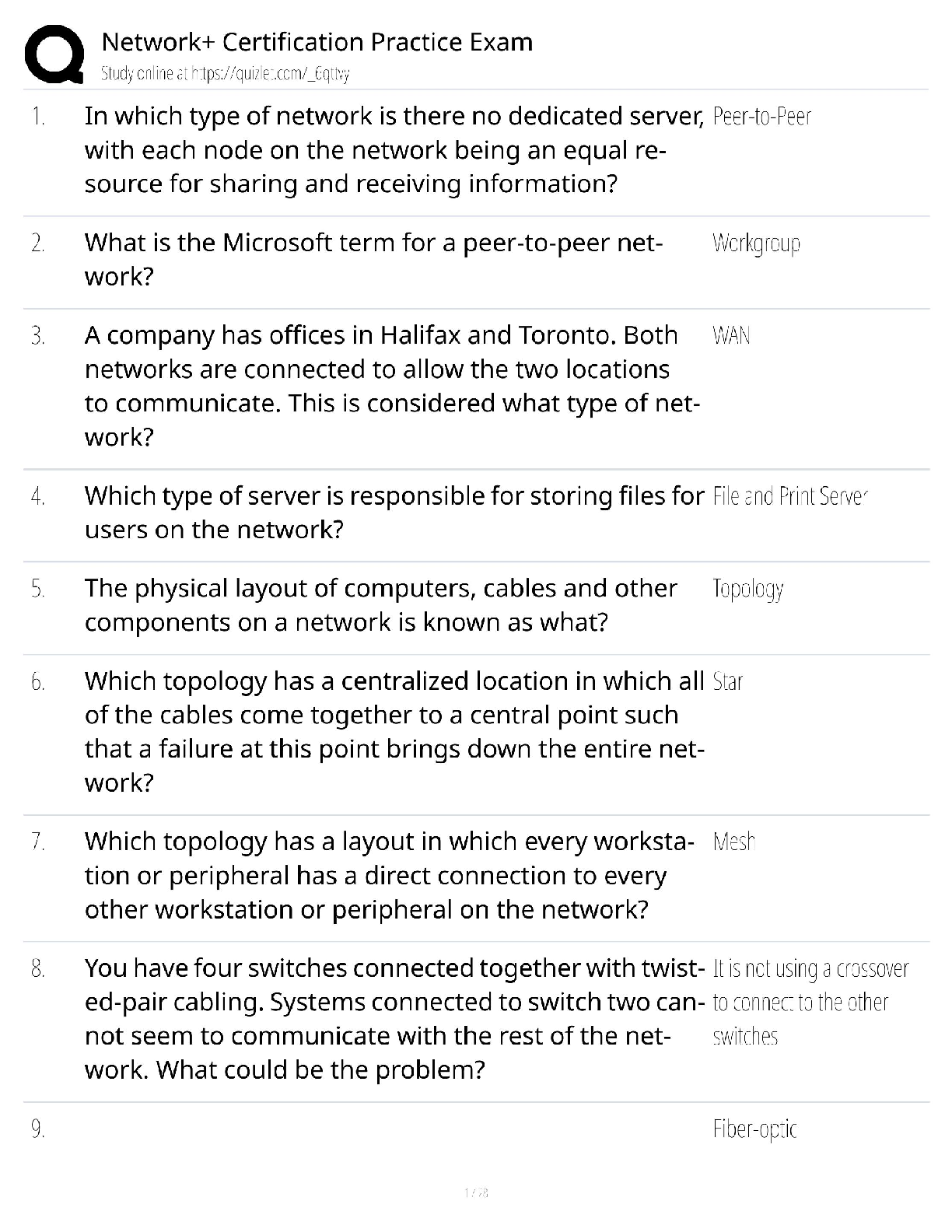
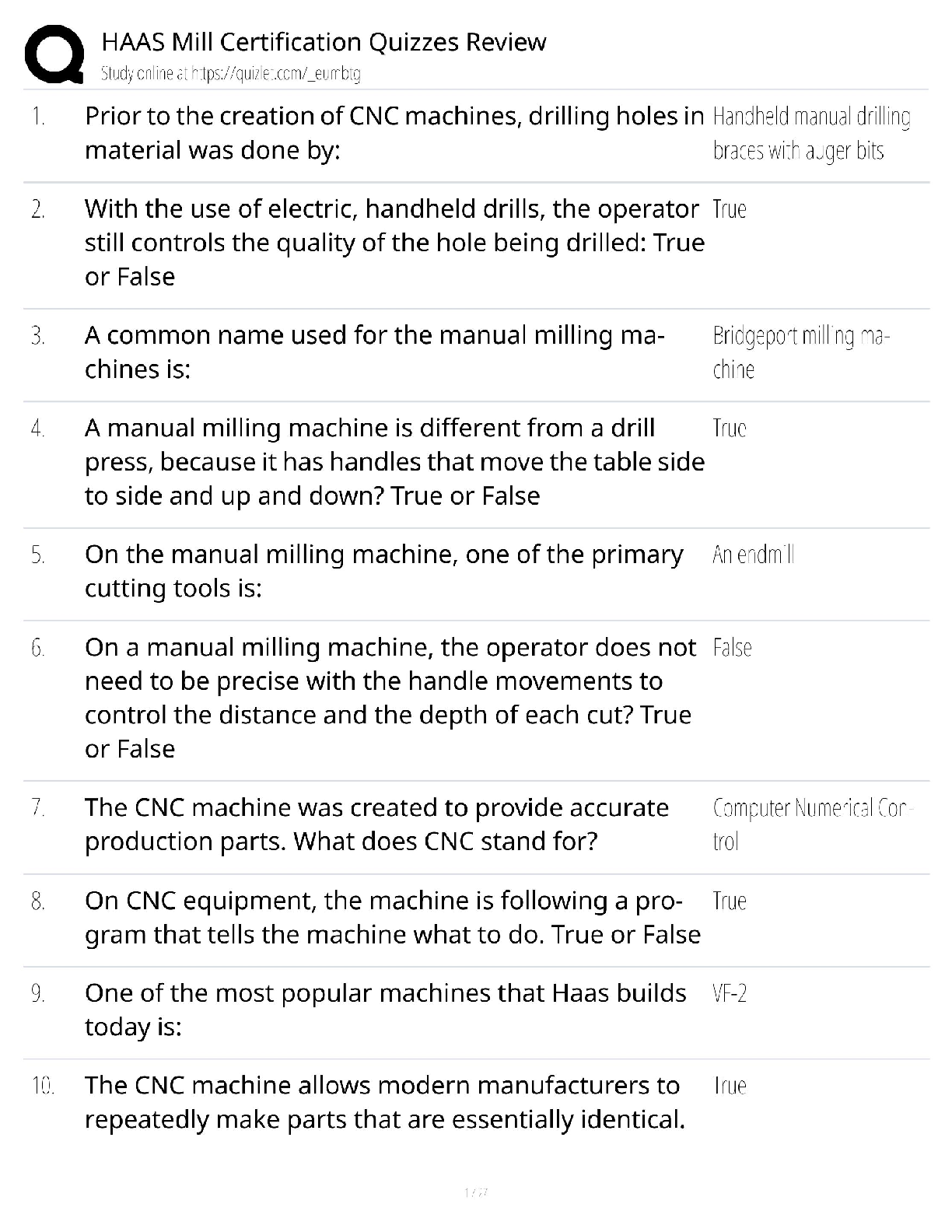
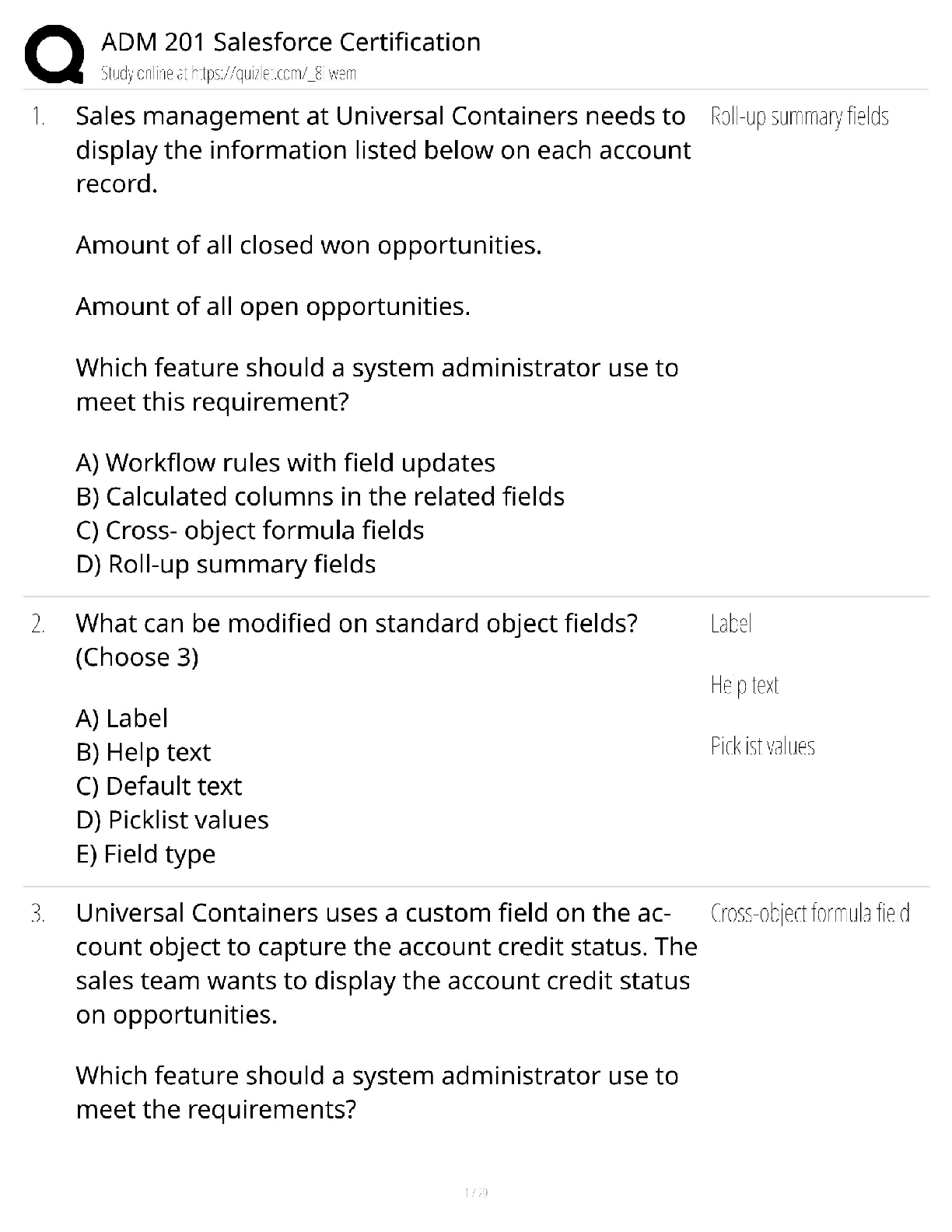
Mathematics > QUESTIONS & ANSWERS > Practice Midterm 2.1.Solutions - Northwestern University MATH 228 (All)

Practice Midterm 2.1.Solutions - Northwestern University MATH 228

Document Content and Description Below

PRACTICE Midterm 2.1 Math 228-1, Spring 2020 1. A cycloid is the curve traced out by a point on a wheel as it rolls. It has the parameterization r(t) = ht − sin t, 1 − costi, 0 ≤ t ≤ 2π F ... ind the arc-length of the cycloid. (Hint: You will need to use the formulas cos t 2 = q 1+cos t 2 and sin t 2 = q 1−cos t 2 .) Solution: We have r 0 (t) = h1 − cost,sin ti. Then for 0 ≤ t ≤ 2π we have |r 0 (t)| = p (1 − cost) 2 + (sin t) 2 = q (1 − 2 cost + cos2 t + sin2 t = p 2 − 2 cost + cos2 t + sin2 t = 2 sin t 2 . Thus the arc-length is Z 2π 0 |r 0 (t)| = Z 2π 0 2 sin t 2 = −4 cos t 2 2π 0 = 8. 2. Show that the center of the osculating circle for the parabola y = x 2 at the point (a, a2 ) is (−4a 3 , 3a 2 + 1 2 ). Solution: r(t) = ht, t2 i v(t) = h1, 2ti |v(t)| = √ 1 + 4t 2 T(t) = 1 √ 1 + 4t 2 , 2t √ 1 + 4t 2 κ(t)N(t) = dT dt 1 |v(t)| = * −4t (1 + 4t 2 ) 3 2 , 2 (1 + 4t 2 ) 3 2 + 1 √ 1 + 4t 2 . From this we can calculate that κ = 2 (1 + 4t 2 ) 3 2 . N(t) = −2t √ 1 + 4t 2 , 1 √ 1 + 4t 2 . Then the center of the osculating circle is distance 1 κ in the direction of N(t) from any point on the curve. r(t) + 1 κ N(t) = ht, t2 i + h−t(1 + 4t 2 ), 1 2 (1 + 4t 2 )i = h−4t 3 , 3t 2 + 1 2 i 3. Let f(x, y, z) = x 2 + [Show More]

Last updated: 3 years ago

Preview 1 out of 3 pages

Buy Now

Instant download

We Accept: