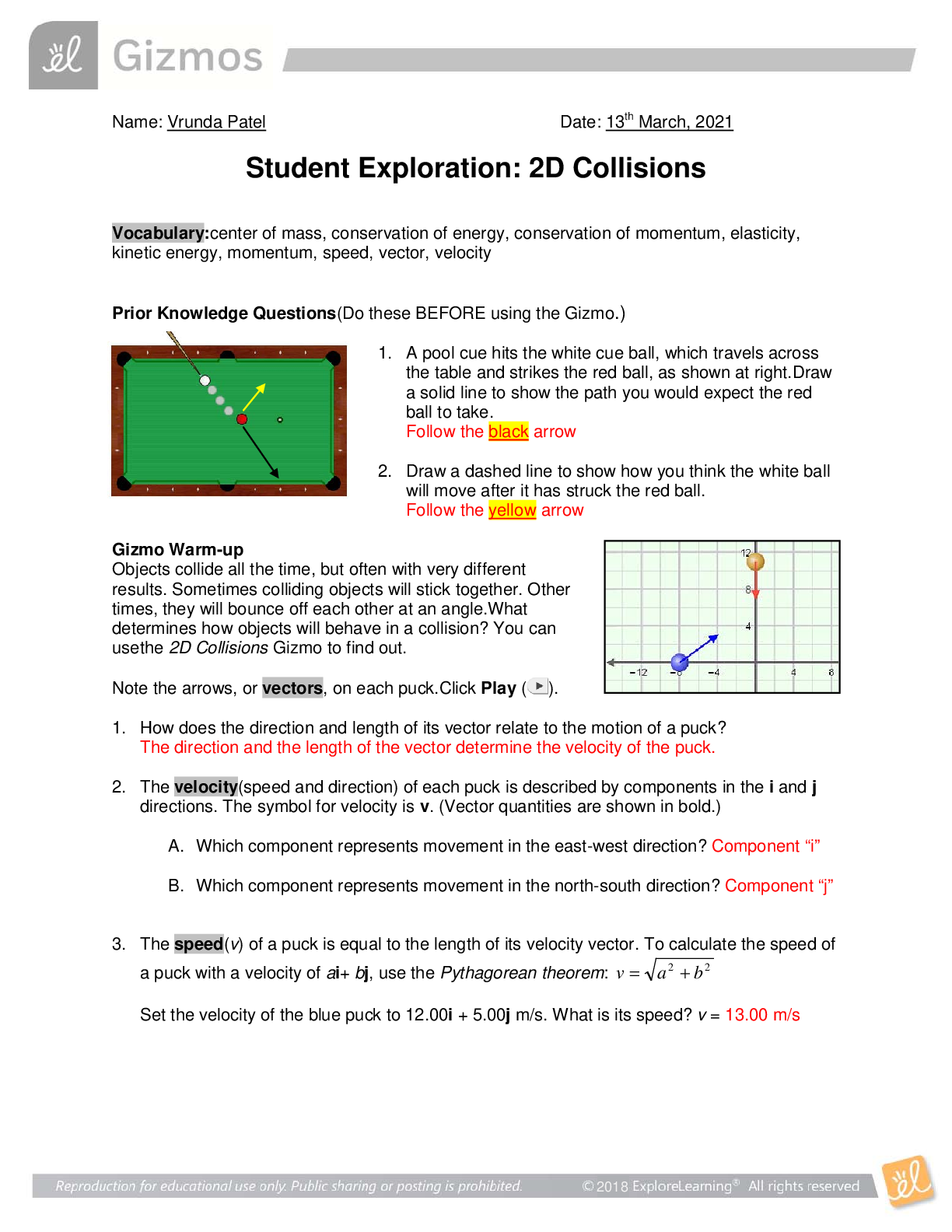
NRNP 6560 – Week 9 Advanced Practice Case Study: Pathophysiologic Analysis, Differential Diagnosis, and Patient-Centered Management of Abdominal Pain
$ 16.5

CS0-002 Exam 2023
$ 20

ITSS 4300 Final Exam
$ 9

SCIENCE 101 4.3.4 Lab: Force of Friction Dry Lab Physics Sem 1 Points Possible: 50
$ 7
.png)
Pearson Edexcel GCE Question Booklet + Mark Scheme (Results) November 2021 Further Mathematics Advanced Level in Further Mathematics Paper 1 9FM0/01
$ 10

Fmst 210 Final Questions With Correct Detailed Answers
$ 16

DAVIS_ADVANTAGE_FOR_PATHOPHYSIOLOGY_2ND_EDITION_CAPRIOTTI_TEST_BANK
$ 15

Test Bank For The Language of Medicine 12th Edition By Davi-Ellen Chabner , All Chapter 1-22, A+ Guide Pdf Newest Version.
$ 20
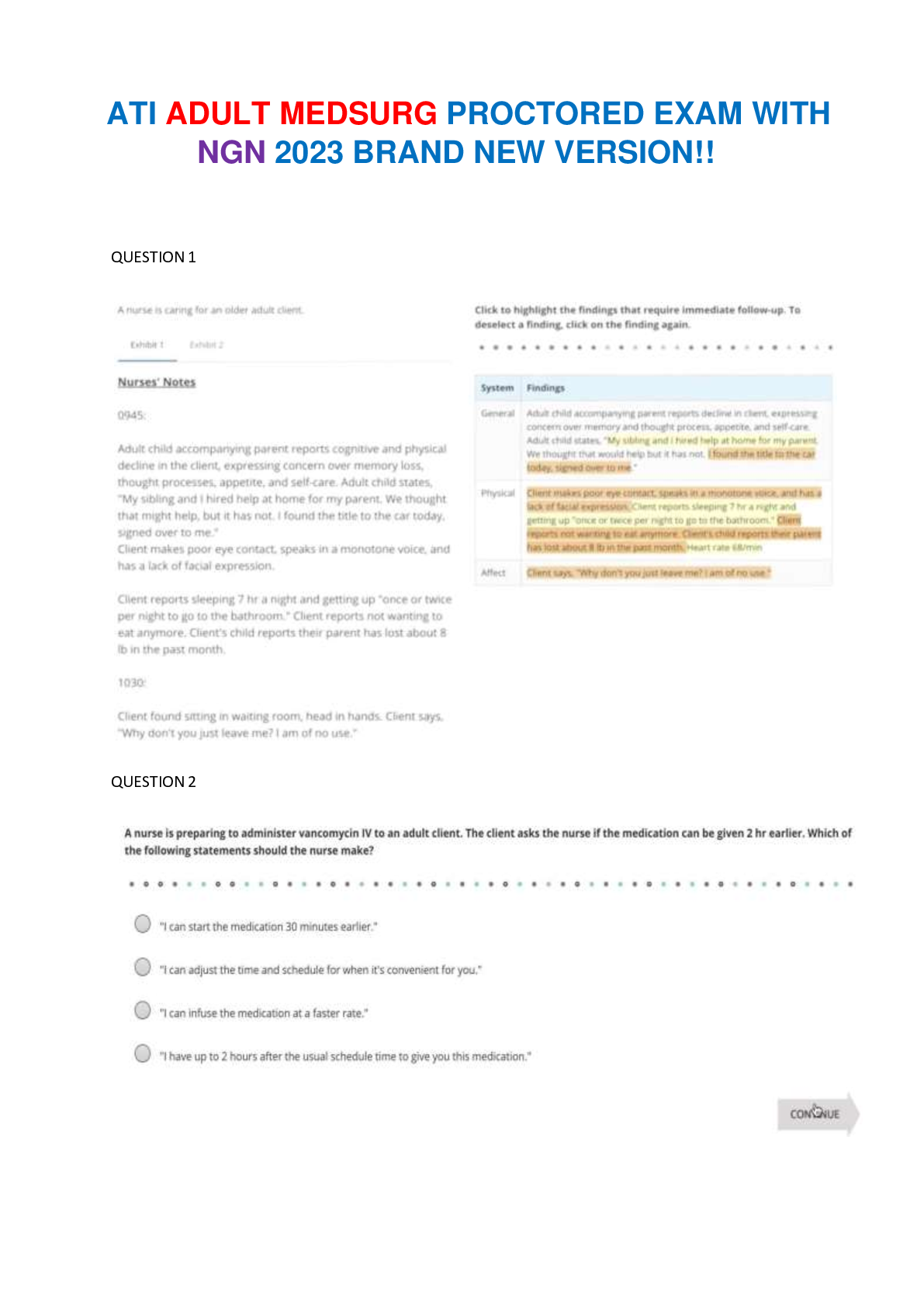
ATI ADULT MEDSURG PROCTORED EXAM WITH NGN 2023 BRAND NEW VERSION!!
$ 26.5

NURS-6501N / NURS 6501: ADVANCED PATHOPHYSIOLOGY FINAL TEST BANK:WALDEN UNIVERSITY(NEWEST-2021))
$ 30
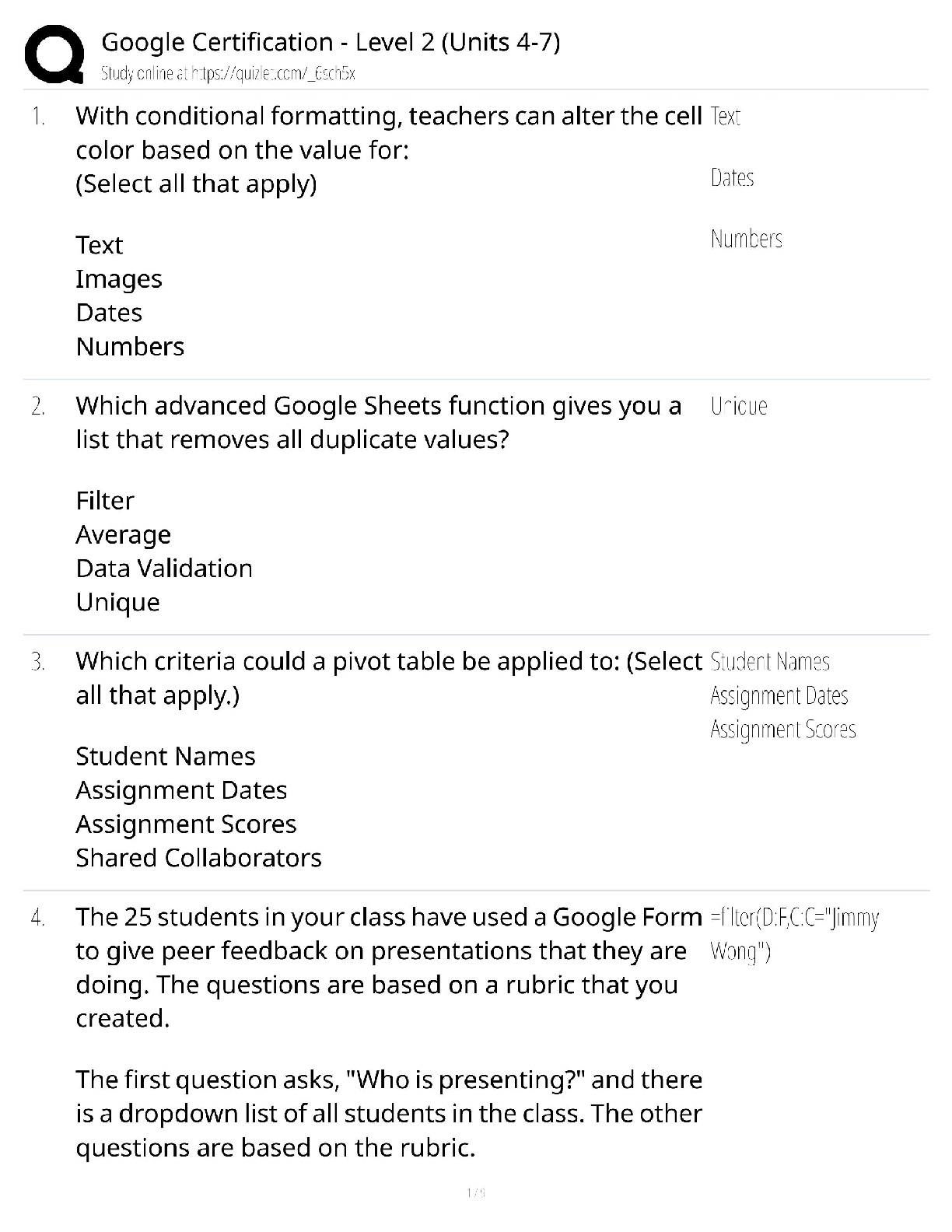
Google Certification Level 2 / Units 4-7 Study Guide / Advanced Digital Skills & Test Bank / Score 100% / 2025 Update
$ 23.5

NR 328 Cancer Quiz | Questions & Answers with rationales
$ 10.5

CA DPR LAWS AND REGULATIONS EXAM ACTUAL EXAM 150 QUESTIONS AND CORRECT DETAILED ANSWERS WITH RATIONALES (VERIFIED ANSWERS) ALREADY GRADED A+
$ 16

NUR 3262L - Exam 2 PEDS, Labor, Birth/ Postpartum: 14, 15, 16 1. Identification and nursing management of each stage of labor Nursing Care During Labor and Birth Nursing Management during the First stage of labor with additional notes 2021 latest Updates.
$ 13

SOCW 6301 Week 6 Assignment Relationship Between Qualitative Analysis and Evidence-Based Practice, complete solution guide - Walden.LATEST 2022
$ 15

NR 509 Midterm Exam 2022 VERIFIED
$ 10

WGU Pathophysiology D236 Exam - Questions and Answers
$ 14
.png)
System Administration and IT Infrastructure Services Questions and Answers Already Passed
$ 7

Advanced Nursing Care Medical Final Exam With Correct Answers 2023.pdf
$ 15
.png)
Home Inspector National Exam Questions and Answers Rated A
$ 15

CR2 Ltd is a multichannel banking software solutions
$ 2

TF-CBT CERT Exam Final Exam 2025/2026 Complete All Verified Questions And Correct Detailed Answers (Rationales) |Already Graded A+||Brand New Updated Version
$ 20

ATI Pharmacology 2019 B STUDY GUIDE
$ 8.5

CIST 2412 - Final Exam QUESTIONS AND ANSWERS(SCORES A+)
$ 9
ati teas nursing entrance exam review test bank 1 .docx (4)
$ 16

TEST BANK Anatomy and Physiology 2nd Edition by OpenStax Chapters 1 - 28, Complete
$ 20

HESI ANATOMY AND PHYSIOLOGY
$ 25

Applied_Pathophysiology_for_the_Advanced_Practice_Nurse,_Second
$ 15

NUR 313 Contemporary Issues in Professional Nursing MIDTERM EXAM 2024.pdf (2)
$ 15

Applied_Pathophysiology_for_the_Advanced_Practice_Nurse,_Second
$ 15
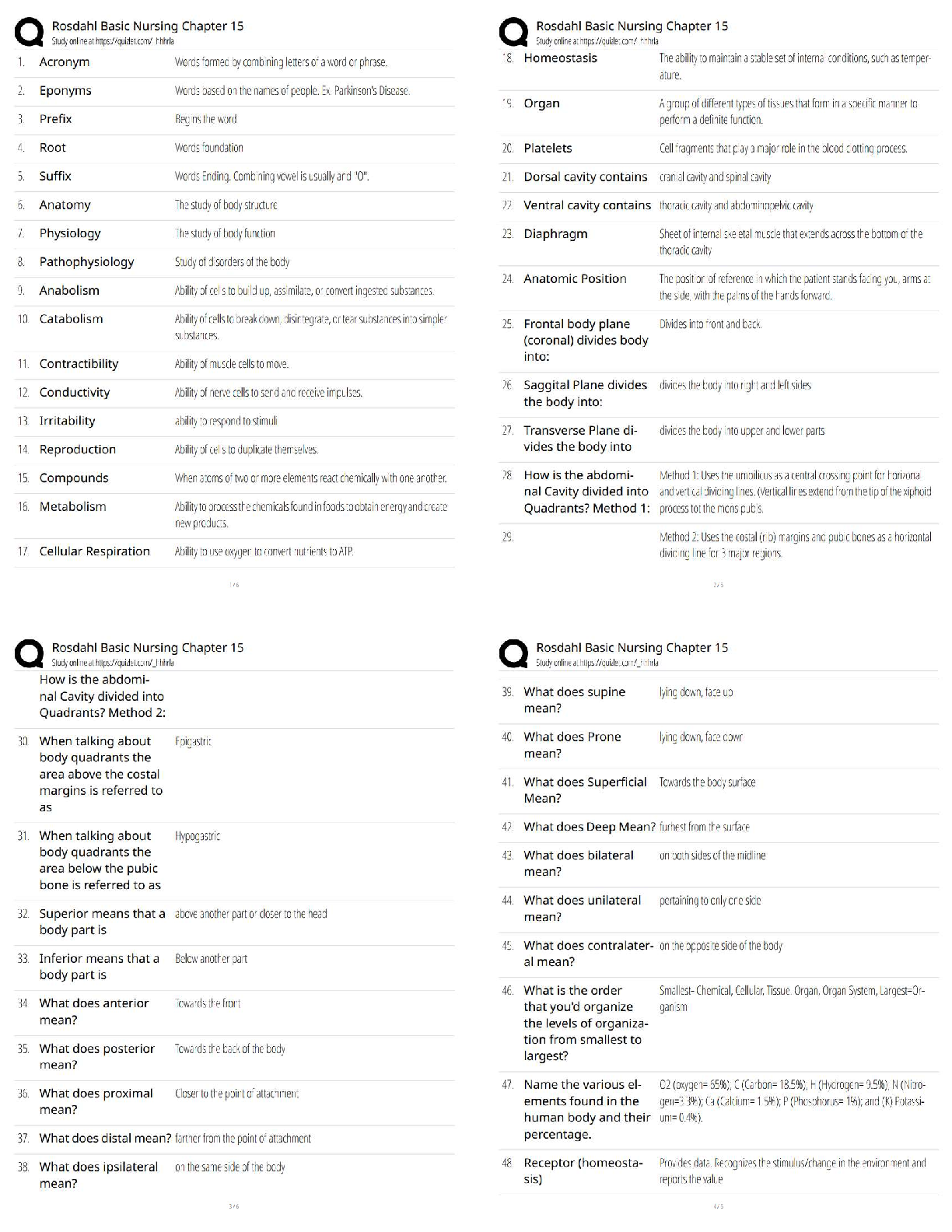
Rosdahl Basic Nursing Chapter 15 | Medication Administration Study Notes / NCLEX Review / 2025 Update
$ 8

TEST BANK Anatomy and Physiology 2nd Edition by OpenStax Chapters 1 - 28, Complete
$ 20

CompTIA A+ Exam 220-1001 and 220- 1002
$ 13
.png)
Home Inspector National Exam Questions and Answers Rated A
$ 15

Test Bank for Anatomy and Physiology, 2nd Edition by OpenStax | All 28 Chapters | Verified Questions & Answers | ISBN: 9781711494067 | Updated 2025
$ 20

NURS 6541 Final Exam 2 – Question and Answers (100 out of 100)
$ 23

NR 510 Week 6 Assignment; APN Professional Development Plan (v2) Graded Top.