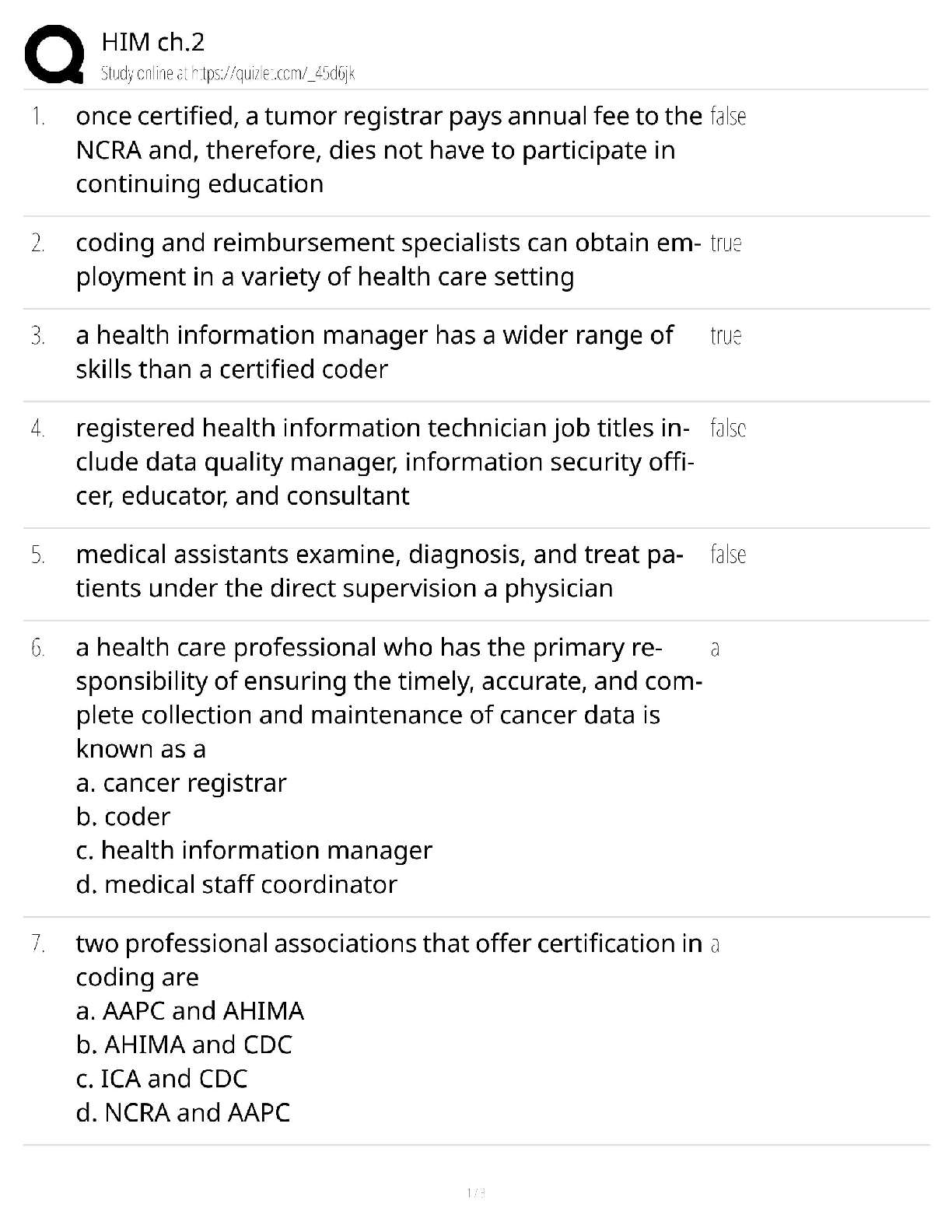
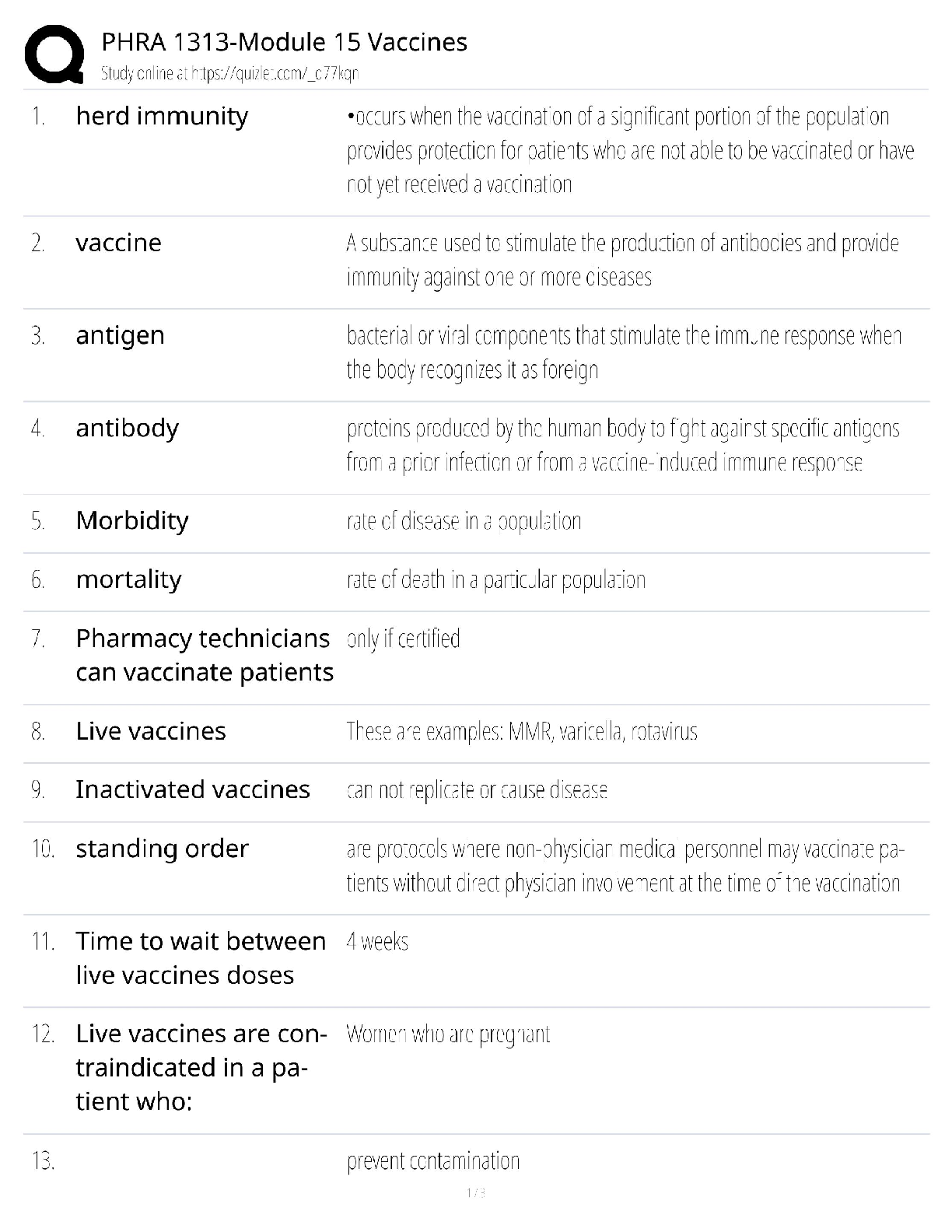
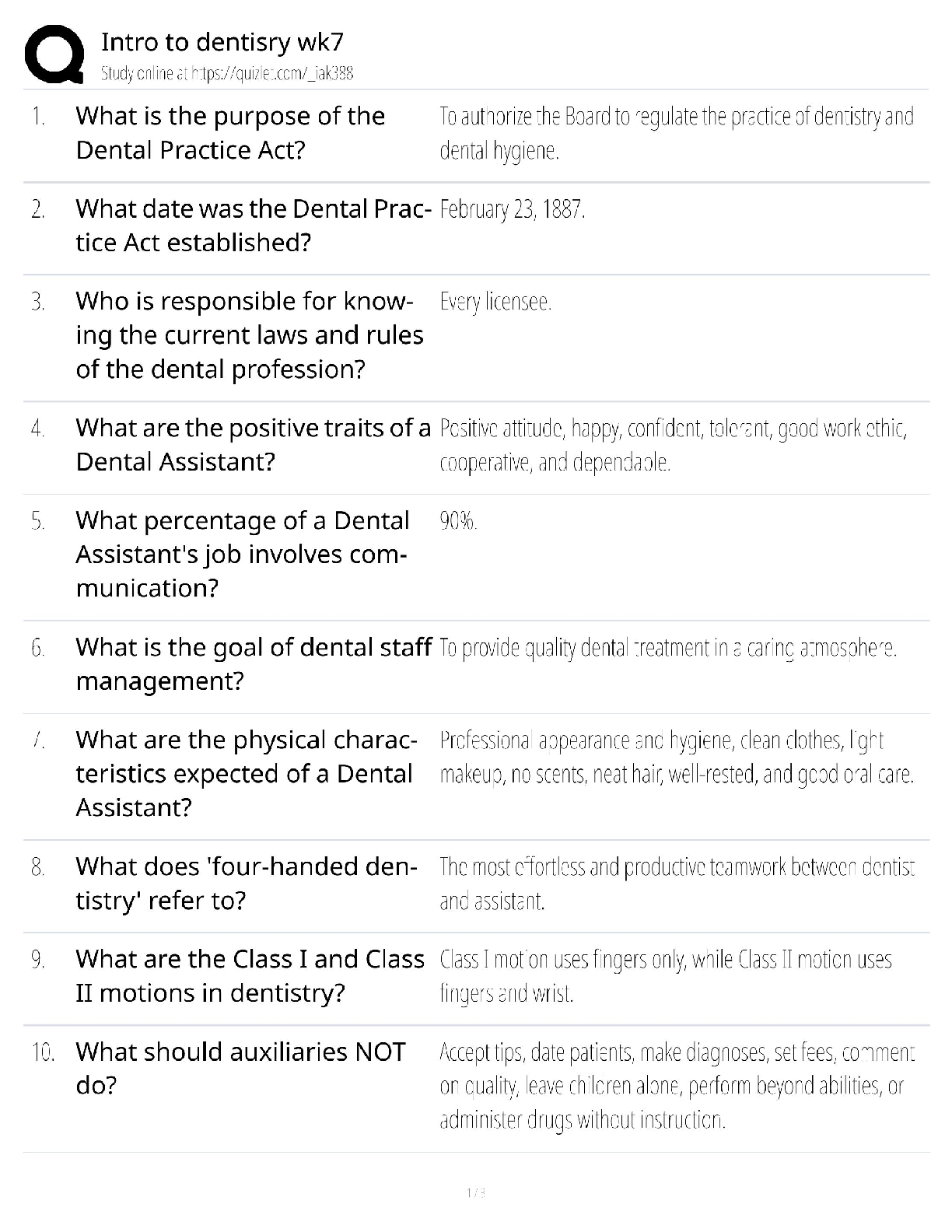
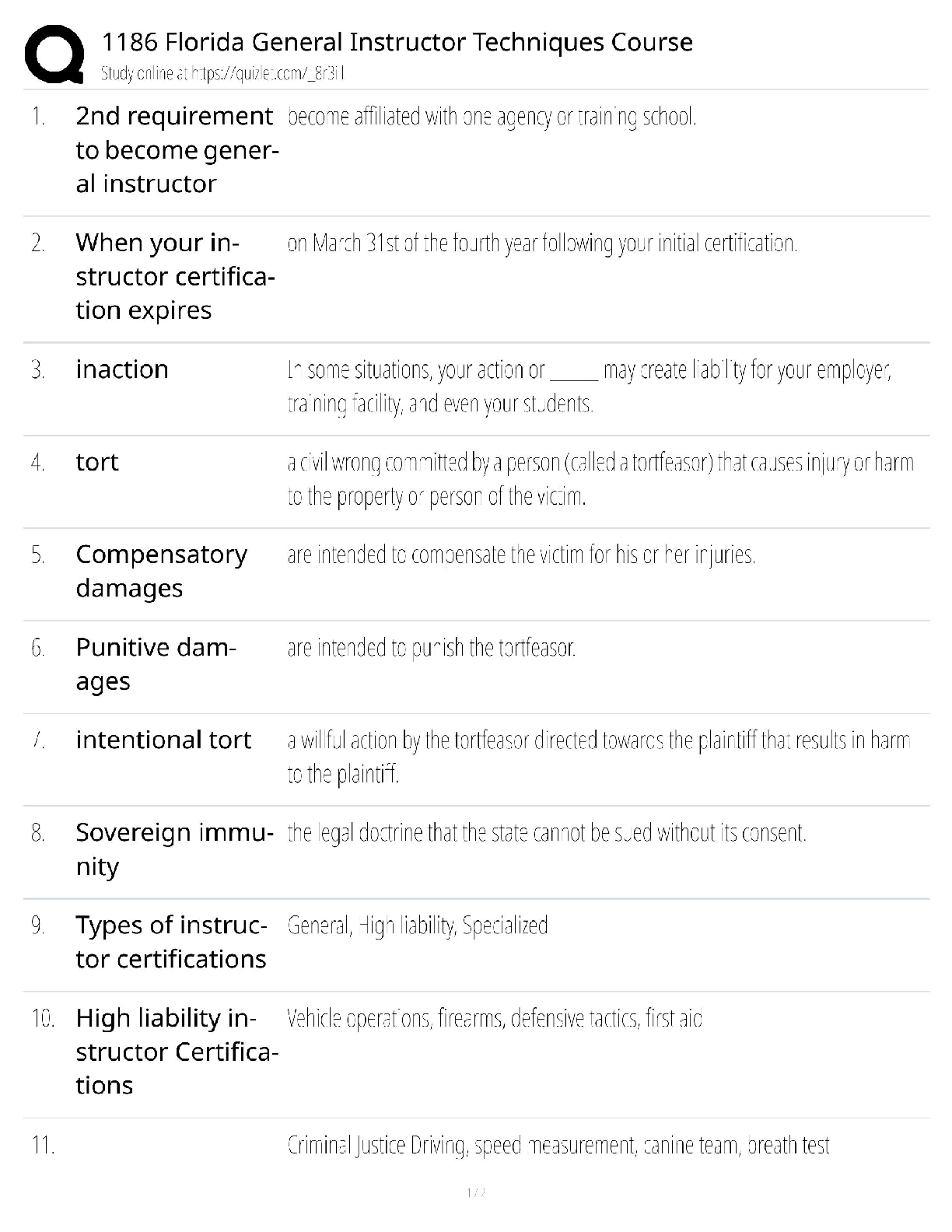
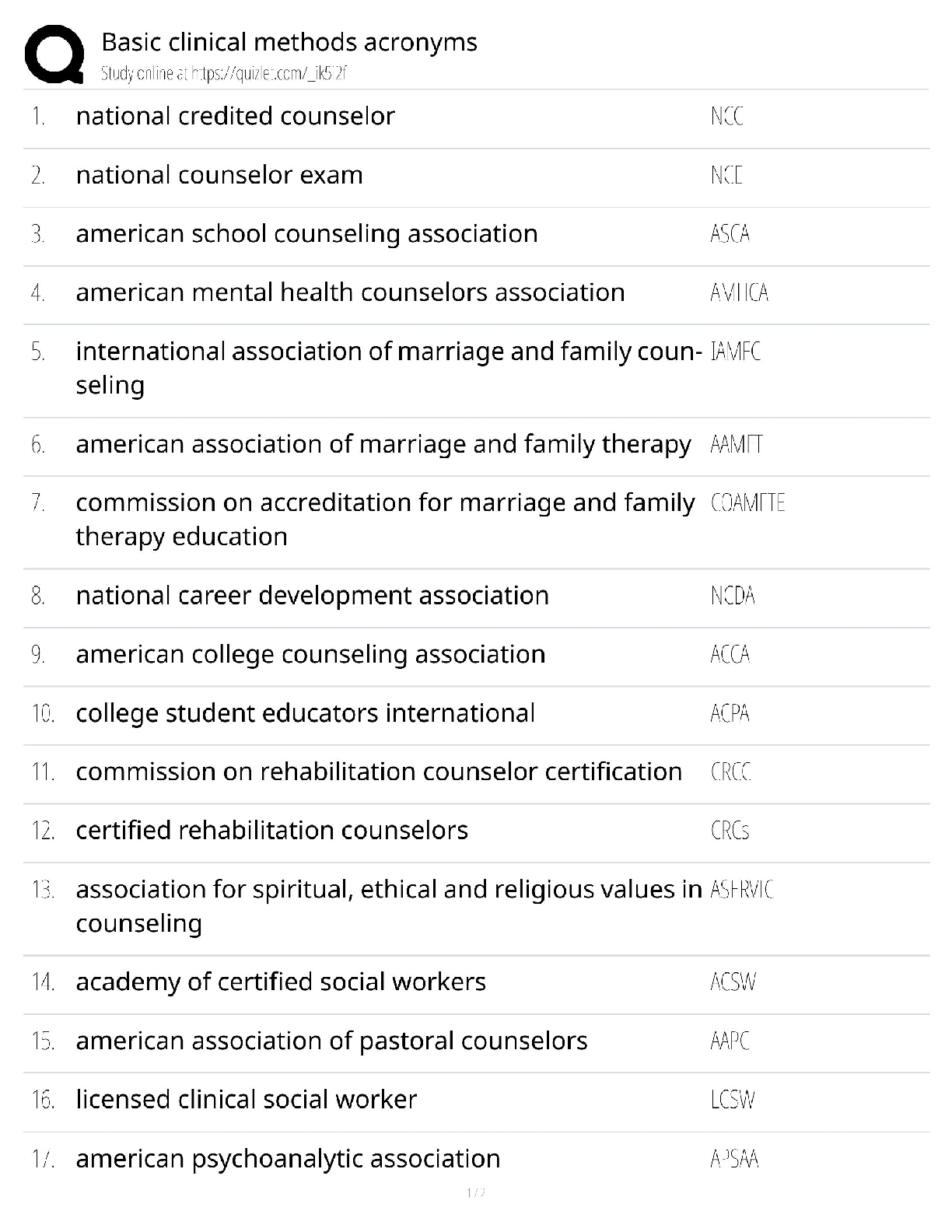
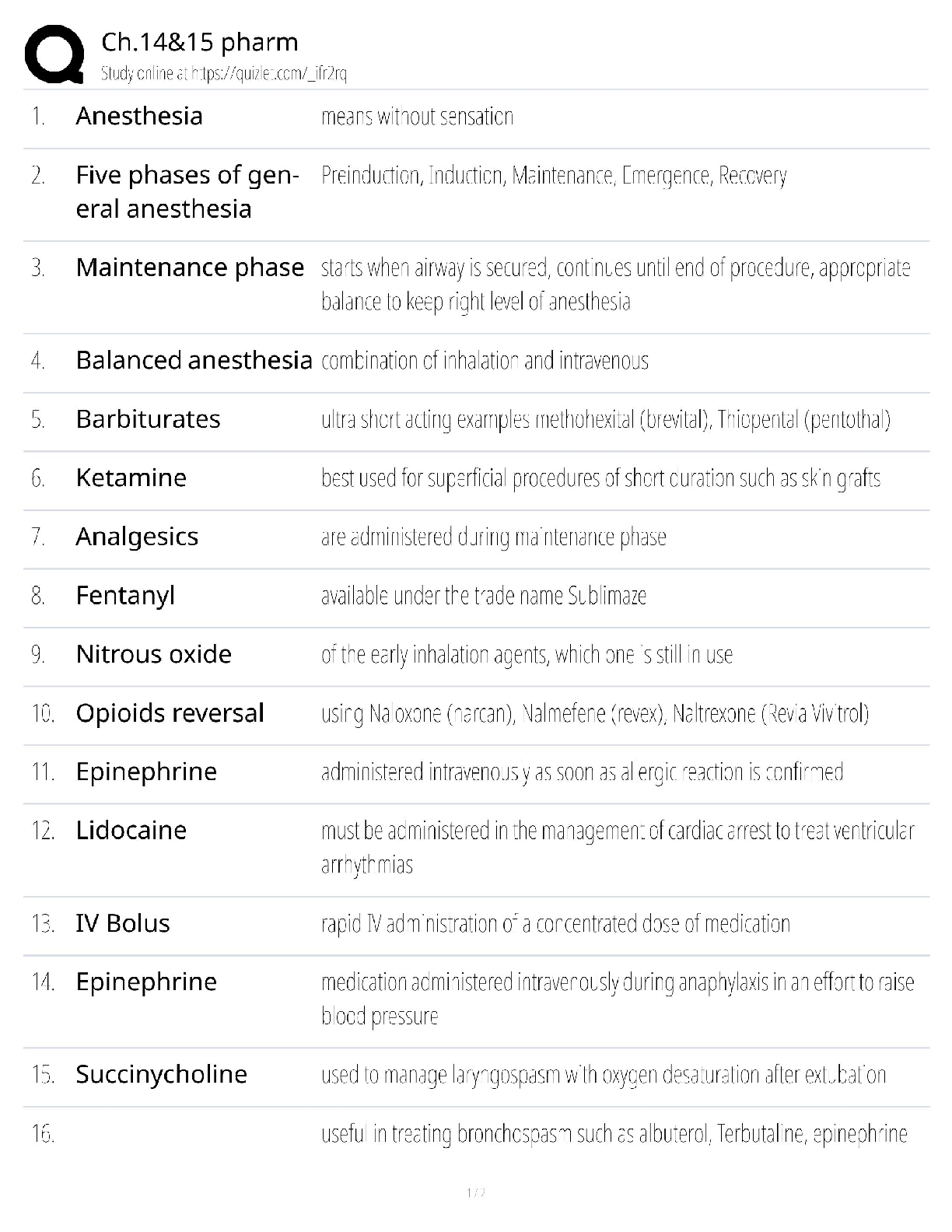
Calculus > QUESTIONS & ANSWERS > Chapter 2: LIMITS AND DERIVATIVES. Work and Answers (All)
Chapter 2: LIMITS AND DERIVATIVES. Work and Answers
Document Content and Description Below
2.1 The Tangent and Velocity Problems 1. (a) Using (15 250), we construct the following table: slope = 5 (5 694) 694 5−−15 250 = − 444 10 = −444 10 (10 44 ... 4) 444 10−−250 15 = − 194 5 = −388 20 (20 111) 111 20−−250 15 = − 139 5 = −278 25 (25 28) 28 25−−250 15 = − 222 10 = −222 30 (30 0) 0 30 −−250 15 = − 250 15 = −166 (b) Using the values of that correspond to the points closest to ( = 10 and = 20), we have −388 + (−278) 2 = −333 (c) From the graph, we can estimate the slope of the tangent line at to be −300 9 = −333. 2. (a) Slope = 2948 42 −− 2530 36 = 418 6 ≈ 6967 (b) Slope = 2948 42 − − 2661 38 = 287 4 = 7175 (c) Slope = 2948 42 −− 2806 40 = 142 2 = 71 (d) Slope = 3080 44 − − 2948 42 = 132 2 = 66 From the data, we see that the patient’s heart rate is decreasing from 71 to 66 heartbeatsminute after 42 minutes. After being stable for a while, the patient’s heart rate is dropping. 3. (a) = 1 1 − , (2 −1) ( 1(1 − )) (i) 15 (15 −2) 2 (ii) 19 (19 −1111 111) 1111 111 (iii) 199 (199 −1010 101) 1010 101 (iv) 1999 (1999 −1001 001) 1001 001 (v) 25 (25 −0666 667) 0666 667 (vi) 21 (21 −0909 091) 0909 091 (vii) 201 (201 −0990 099) 0990 099 (viii) 2001 (2001 −0999 001) 0999 001 (b) The slope appears to be 1. (c) Using = 1, an equation of the tangent line to the curve at (2 −1) is − (−1) = 1( − 2), or = − 3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 67 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.68 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 4. (a) = cos , (05 0) (i) 0 (0 1) −2 (ii) 04 (04 0309017) −3090170 (iii) 049 (049 0031411) −3141076 (iv) 0499 (0499 0003142) −3141587 (v) 1 (1 −1) −2 (vi) 06 (06 −0309017) −3090170 (vii) 051 (051 −0031411) −3141076 (viii) 0501 (0501 −0003142) −3141587 (b) The slope appears to be −. (c) − 0 = −( − 05) or = − + 1 2. (d) 5. (a) = () = 40 − 162. At = 2, = 40(2) − 16(2)2 = 16. The average velocity between times 2 and 2 + is ave = (2 + ) − (2) (2 + ) − 2 = 40(2 + ) − 16(2 + )2 − 16 = −24 − 162 = −24 − 16, if 6= 0. (i) [2 25]: = 05, ave = −32 fts (ii) [2 21]: = 01, ave = −256 fts (iii) [2 205]: = 005, ave = −248 fts (iv) [2 201]: = 001, ave = −2416 fts (b) The instantaneous velocity when = 2 ( approaches 0) is −24 fts. 6. (a) = () = 10 − 1862. At = 1, = 10(1) − 186(1)2 = 814. The average velocity between times 1 and 1 + is ave = (1 + ) − (1) (1 + ) − 1 = 10(1 + ) − 186(1 + )2 − 814 = 628 − 1862 = 628 − 186, if 6= 0. (i) [1 2]: = 1, ave = 442 ms (ii) [1 15]: = 05, ave = 535 ms (iii) [1 11]: = 01, ave = 6094 ms (iv) [1 101]: = 001, ave = 62614 ms (v) [1 1001]: = 0001, ave = 627814 ms (b) The instantaneous velocity when = 1 ( approaches 0) is 628 ms. 7. (a) (i) On the interval [2 4] , ave = (4) − (2) 4 − 2 = 792 − 206 2 = 293 fts. (ii) On the interval [3 4] , ave = (4) − (3) 4 − 3 = 792 − 465 1 = 327 fts. (iii) On the interval [4 5] , ave = (5) − (4) 5 − 4 = 1248 − 792 1 = 456 fts. (iv) On the interval [4 6] , ave = (6) − (4) 6 − 4 = 1767 − 792 2 = 4875 fts. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.1 THE TANGENT AND VELOCITY PROBLEMS ¤ 69 (b) Using the points (2 16) and (5 105) from the approximate tangent line, the instantaneous velocity at = 3 is about 105 − 16 5 − 2 = 89 3 ≈ 297 fts. 8. (a) (i) = () = 2 sin + 3 cos . On the interval [1 2], ave = (2) − (1) 2 − 1 = 3 − (−3) 1 = 6 cms. (ii) On the interval [1 11], ave = (11) − (1) 11 − 1 ≈ −3471 − (−3) 01 = −471 cms. (iii) On the interval [1 101], ave = (101) − (1) 101 − 1 ≈ −30613 − (−3) 001 = −613 cms. (iv) On the interval [1 1001], ave = (1001) − (1) 1001 − 1 ≈ −300627 − (−3) 0001 = −627 cms. (b) The instantaneous velocity of the particle when = 1 appears to be about −63 cms. 9. (a) For the curve = sin(10) and the point (1 0): 2 (2 0) 0 15 (15 08660) 17321 14 (14 −04339) −10847 13 (13 −08230) −27433 12 (12 08660) 43301 11 (11 −02817) −28173 05 (05 0) 0 06 (06 08660) −21651 07 (07 07818) −26061 08 (08 1) −5 09 (09 −03420) 34202 As approaches 1, the slopes do not appear to be approaching any particular value. (b) We see that problems with estimation are caused by the frequent oscillations of the graph. The tangent is so steep at that we need to take -values much closer to 1 in order to get accurate estimates of its slope. (c) If we choose = 1001, then the point is (1001 −00314) and ≈ −313794. If = 0999, then is (0999 00314) and = −314422. The average of these slopes is −314108. So we estimate that the slope of the tangent line at is about −314. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.70 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 2.2 The Limit of a Function 1. As approaches 2, () approaches 5. [Or, the values of () can be made as close to 5 as we like by taking sufficiently close to 2 (but 6= 2).] Yes, the graph could have a hole at (2 5) and be defined such that (2) = 3. 2. As approaches 1 from the left, () approaches 3; and as approaches 1 from the right, () approaches 7. No, the limit does not exist because the left- and right-hand limits are different. 3. (a) lim →−3 () = ∞ means that the values of () can be made arbitrarily large (as large as we please) by taking sufficiently close to −3 (but not equal to −3). (b) lim →4+ () = −∞ means that the values of () can be made arbitrarily large negative by taking sufficiently close to 4 through values larger than 4. 4. (a) As approaches 2 from the left, the values of () approach 3, so lim →2− () = 3. (b) As approaches 2 from the right, the values of () approach 1, so lim →2+ () = 1. (c) lim →2 () does not exist since the left-hand limit does not equal the right-hand limit. (d) When = 2, = 3, so (2) = 3. (e) As approaches 4, the values of () approach 4, so lim →4 () = 4. (f ) There is no value of () when = 4, so (4) does not exist. 5. (a) As approaches 1, the values of () approach 2, so lim →1 () = 2. (b) As approaches 3 from the left, the values of () approach 1, so lim →3− () = 1. (c) As approaches 3 from the right, the values of () approach 4, so lim →3+ () = 4. (d) lim →3 () does not exist since the left-hand limit does not equal the right-hand limit. (e) When = 3, = 3, so (3) = 3. 6. (a) () approaches 4 as approaches −3 from the left, so lim →−3− () = 4. (b) () approaches 4 as approaches −3 from the right, so lim →−3+ () = 4. (c) lim →−3 () = 4 because the limits in part (a) and part (b) are equal. (d) (−3) is not defined, so it doesn’t exist. (e) () approaches 1 as approaches 0 from the left, so lim →0− () = 1. (f ) () approaches −1 as approaches 0 from the right, so lim →0+ () = −1. (g) lim →0 () does not exist because the limits in part (e) and part (f ) are not equal. (h) (0) = 1 since the point (0 1) is on the graph of . (i) Since lim →2− () = 2 and lim →2+ () = 2, we have lim →2 () = 2. (j) (2) is not defined, so it doesn’t exist. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.2 THE LIMIT OF A FUNCTION ¤ 71 (k) () approaches 3 as approaches 5 from the right, so lim →5+ () = 3. (l) () does not approach any one number as approaches 5 from the left, so lim →5− () does not exist. 7. (a) lim →0− () = −1 (b) lim →0+ () = −2 (c) lim →0 () does not exist because the limits in part (a) and part (b) are not equal. (d) lim →2− () = 2 (e) lim →2+ () = 0 (f) lim →2 () does not exist because the limits in part (d) and part (e) are not equal. (g) (2) = 1 (h) lim →4 () = 3 8. (a) lim →−3 () = ∞ (b) lim →2 () does not exist. (c) lim →2− () = −∞ (d) lim →2+ () = ∞ (e) lim →−1 () = −∞ (f) The equations of the vertical asymptotes are = −3, = −1 and = 2. 9. (a) lim →−7 () = −∞ (b) lim →−3 () = ∞ (c) lim →0 () = ∞ (d) lim →6− () = −∞ (e) lim →6+ () = ∞ (f) The equations of the vertical asymptotes are = −7, = −3, = 0, and = 6. 10. lim →12− () = 150 mg and lim →12+ () = 300 mg. These limits show that there is an abrupt change in the amount of drug in the patient’s bloodstream at = 12 h. The left-hand limit represents the amount of the drug just before the fourth injection. The right-hand limit represents the amount of the drug just after the fourth injection. 11. From the graph of () = 1 + if −1 2 if −1 ≤ 1 2 − if ≥ 1 , we see that lim → () exists for all except = −1. Notice that the right and left limits are different at = −1. 12. From the graph of () = 1 + sin if 0 cos if 0 ≤ ≤ sin if , we see that lim → () exists for all except = . Notice that the right and left limits are different at = . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.72 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 13. (a) lim →0− () = 1 (b) lim →0+ () = 0 (c) lim →0 () does not exist because the limits in part (a) and part (b) are not equal. 14. (a) lim →0− () = −1 (b) lim →0+ () = 1 (c) lim →0 () does not exist because the limits in part (a) and part (b) are not equal. 15. lim →0− () = −1, lim →0+ () = 2, (0) = 1 16. lim →0 () = 1, lim →3− () = −2, lim →3+ () = 2, (0) = −1, (3) = 1 17. lim →3+ () = 4, lim →3− () = 2, lim →−2 () = 2, (3) = 3, (−2) = 1 18. lim →0− () = 2, lim →0+ () = 0, lim →4− () = 3, lim →4+ () = 0, (0) = 2, (4) = 1 19. For () = 2 − 3 2 − 9 : () 31 0508 197 305 0504 132 301 0500 832 3001 0500 083 30001 0500 008 () 29 0491 525 295 0495 798 299 0499 165 2999 0499 917 29999 0499 992 It appears that lim →3 2 − 3 2 − 9 = 1 2 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.2 THE LIMIT OF A FUNCTION ¤ 73 20. For () = 2 − 3 2 − 9 : () −25 −5 −29 −29 −295 −59 −299 −299 −2999 −2999 −29999 −29,999 () −35 7 −31 31 −305 61 −301 301 −3001 3001 −30001 30,001 It appears that lim →−3+ () = −∞ and that lim →−3− () = ∞, so lim →−3 2 − 3 2 − 9 does not exist. 21. For () = 5 − 1 : () 05 22364 988 01 6487 213 001 5127 110 0001 5012 521 00001 5001 250 () −05 1835 830 −01 3934 693 −001 4877 058 −0001 4987 521 −00001 4998 750 It appears that lim →0 5 − 1 = 5. 22. For () = (2 + )5 − 32 : () 05 131312 500 01 88410 100 001 80804 010 0001 80080 040 00001 80008 000 () −05 48812 500 −01 72390 100 −001 79203 990 −0001 79920 040 −00001 79992 000 It appears that lim →0 (2 + )5 − 32 = 80. 23. For () = ln − ln 4 − 4 : () 39 0253 178 399 0250 313 3999 0250 031 39999 0250 003 () 41 0246 926 401 0249 688 4001 0249 969 40001 0249 997 It appears that lim →4 () = 025. The graph confirms that result. 24. For () = 1 + 9 1 + 15 : () −11 0427 397 −101 0582 008 −1001 0598 200 −10001 0599 820 () −09 0771 405 −099 0617 992 −0999 0601 800 −09999 0600 180 It appears that lim →−1 () = 06. The graph confirms that result. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.74 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 25. For () = sin 3 tan 2 : () ±01 1457 847 ±001 1499 575 ±0001 1499 996 ±00001 1500 000 It appears that lim →0 sin 3 tan 2 = 15. The graph confirms that result. 26. For () = 5 − 1 : () 01 1746 189 001 1622 459 0001 1610 734 00001 1609 567 () −01 1486 601 −001 1596 556 −0001 1608 143 −00001 1609 308 It appears that lim →0 () ≈ 16094. The graph confirms that result. 27. For () = : () 01 0794 328 001 0954 993 0001 0993 116 00001 0999 079 It appears that lim →0+ () = 1. The graph confirms that result. 28. For () = 2 ln : () 01 −0023 026 001 −0000 461 0001 −0000 007 00001 −0000 000 It appears that lim →0+ () = 0. The graph confirms that result. 29. (a) From the graphs, it seems that lim →0 cos 2 − cos 2 = −15. (b) () ±01 −1493 759 ±001 −1499 938 ±0001 −1499 999 ±00001 −1500 000 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.2 THE LIMIT OF A FUNCTION ¤ 75 30. (a) From the graphs, it seems that lim →0 sin sin = 032. (b) () ±01 0323 068 ±001 0318 357 ±0001 0318 310 ±00001 0318 310 Later we will be able to show that the exact value is 1 . 31. lim →5+ + 1 − 5 = ∞ since the numerator is positive and the denominator approaches 0 from the positive side as → 5+. 32. lim →5− + 1 − 5 = −∞ since the numerator is positive and the denominator approaches 0 from the negative side as → 5−. 33. lim →1 2 − ( − 1)2 = ∞ since the numerator is positive and the denominator approaches 0 through positive values as → 1. 34. lim →3− √ ( − 3)5 = −∞ since the numerator is positive and the denominator approaches 0 from the negative side as → 3−. 35. Let = 2 − 9. Then as → 3+, → 0+, and lim →3+ ln(2 − 9) = lim →0+ ln = −∞ by (5). 36. lim →0+ ln(sin ) = −∞ since sin → 0+ as → 0+. 37. lim →(2)+ 1 sec = −∞ since 1 is positive and sec → −∞ as → (2)+. 38. lim →− cot = lim →− cos sin = −∞ since the numerator is negative and the denominator approaches 0 through positive values as → −. 39. lim →2− csc = lim →2− sin = −∞ since the numerator is positive and the denominator approaches 0 through negative values as → 2−. 40. lim →2− 2 − 2 2 − 4 + 4 = lim →2− ((−−2)2) 2 = lim →2− − 2 = −∞ since the numerator is positive and the denominator approaches 0 through negative values as → 2−. 41. lim →2+ 2 − 2 − 8 2 − 5 + 6 = lim →2+ ( ( − − 4)( 3)( + 2) − 2) = ∞ since the numerator is negative and the denominator approaches 0 through negative values as → 2+. 42. lim →0+ 1 − ln = ∞ since 1 → ∞ and ln → −∞ as → 0+. 43. lim →0 (ln 2 − −2) = −∞ since ln 2 → −∞ and −2 → ∞ as → 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.76 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 44. (a) The denominator of = 2 + 1 3 − 22 = 2 + 1 (3 − 2) is equal to zero when = 0 and = 3 2 (and the numerator is not), so = 0 and = 15 are vertical asymptotes of the function. (b) 45. (a) () = 1 3 − 1. From these calculations, it seems that lim →1− () = −∞ and lim →1+ () = ∞. () 05 −114 09 −369 099 −337 0999 −3337 09999 −33337 099999 −33,3337 () 15 042 11 302 101 330 1001 3330 10001 33330 100001 33,3333 (b) If is slightly smaller than 1, then 3 − 1 will be a negative number close to 0, and the reciprocal of 3 − 1, that is, (), will be a negative number with large absolute value. So lim →1− () = −∞. If is slightly larger than 1, then 3 − 1 will be a small positive number, and its reciprocal, (), will be a large positive number. So lim →1+ () = ∞. (c) It appears from the graph of that lim →1− () = −∞ and lim →1+ () = ∞. 46. (a) From the graphs, it seems that lim →0 tan 4 = 4. (b) () ±01 4227 932 ±001 4002 135 ±0001 4000 021 ±00001 4000 000 47. (a) Let () = (1 + )1. () −0001 271964 −00001 271842 −000001 271830 −0000001 271828 0000001 271828 000001 271827 00001 271815 0001 271692 It appears that lim →0 (1 + )1 ≈ 271828, which is approximately . In Section 3.6 we will see that the value of the limit is exactly . (b) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.2 THE LIMIT OF A FUNCTION ¤ 77 48. (a) No, because the calculator-produced graph of () = + ln | − 4| looks like an exponential function, but the graph of has an infinite discontinuity at = 4. A second graph, obtained by increasing the numpoints option in Maple, begins to reveal the discontinuity at = 4. (b) There isn’t a single graph that shows all the features of . Several graphs are needed since looks like ln | − 4| for large negative values of and like for 5, but yet has the infinite discontiuity at = 4. A hand-drawn graph, though distorted, might be better at revealing the main features of this function. 49. For () = 2 − (21000): (a) () 1 0998 000 08 0638 259 06 0358 484 04 0158 680 02 0038 851 01 0008 928 005 0001 465 It appears that lim →0 () = 0. (b) () 004 0000 572 002 −0000 614 001 −0000 907 0005 −0000 978 0003 −0000 993 0001 −0001 000 It appears that lim →0 () = −0001. 50. For () = tan − 3 : (a) () 10 0557 407 73 05 0370 419 92 01 0334 672 09 005 0333 667 00 001 0333 346 67 0005 0333 336 67 (b) It seems that lim →0 () = 1 3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.78 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (c) () 0001 0333 333 50 00005 0333 333 44 00001 0333 330 00 000005 0333 336 00 000001 0333 000 00 0000001 0000 000 00 Here the values will vary from one calculator to another. Every calculator will eventually give false values. (d) As in part (c), when we take a small enough viewing rectangle we get incorrect output. 51. No matter how many times we zoom in toward the origin, the graphs of () = sin() appear to consist of almost-vertical lines. This indicates more and more frequent oscillations as → 0. 52. (a) For any positive integer , if = 1 , then () = tan 1 = tan() = 0. (Remember that the tangent function has period .) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS ¤ 79 (b) For any nonnegative number , if = 4 (4 + 1) , then () = tan 1 = tan (4 + 1) 4 = tan 4 4 + 4 = tan + 4 = tan 4 = 1 (c) From part (a), () = 0 infinitely often as → 0. From part (b), () = 1 infinitely often as → 0. Thus, lim →0 tan 1 does not exist since () does not get close to a fixed number as → 0. 53. There appear to be vertical asymptotes of the curve = tan(2 sin ) at ≈ ±090 and ≈ ±224. To find the exact equations of these asymptotes, we note that the graph of the tangent function has vertical asymptotes at = 2 + . Thus, we must have 2 sin = 2 + , or equivalently, sin = 4 + 2 . Since −1 ≤ sin ≤ 1, we must have sin = ± 4 and so = ± sin−1 4 (corresponding to ≈ ±090). Just as 150◦ is the reference angle for 30◦, − sin−1 4 is the reference angle for sin−1 4 . So = ± − sin−1 4 are also equations of vertical asymptotes (corresponding to ≈ ±224). 54. lim →− = lim →− 0 1 − 22 . As → −, 1 − 22 → 0+, and → ∞. 55. (a) Let = √3−−11. From the table and the graph, we guess that the limit of as approaches 1 is 6. 099 5925 31 0999 5992 50 09999 5999 25 101 6075 31 1001 6007 50 10001 6000 75 (b) We need to have 55 √3−−11 65. From the graph we obtain the approximate points of intersection (09314 55) and (10649 65). Now 1 − 09314 = 00686 and 10649 − 1 = 00649, so by requiring that be within 00649 of 1, we ensure that is within 05 of 6. 2.3 Calculating Limits Using the Limit Laws 1. (a) lim →2 [() + 5()] = lim →2 () + lim →2 [5()] [Limit Law 1] = lim →2 () + 5 lim →2 () [Limit Law 3] = 4 + 5(−2) = −6 (b) lim →2 [()]3 = lim →2 ()3 [Limit Law 6] = ( −2)3 = −8 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.80 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (c) lim →2 () = lim →2 () [Limit Law 11] = √4 = 2 (d) lim →2 3() () = lim →2 [3()] lim →2 () [Limit Law 5] = 3 lim →2 () lim →2 () [Limit Law 3] = 3(4) −2 = −6 (e) Because the limit of the denominator is 0, we can’t use Limit Law 5. The given limit, lim →2 () (), does not exist because the denominator approaches 0 while the numerator approaches a nonzero number. (f) lim →2 () () () = lim →2 [() ()] lim →2 () [Limit Law 5] = lim →2 () · lim →2 () lim →2 () [Limit Law 4] = −2 · 0 4 = 0 2. (a) lim →2 [() + ()] = lim →2 () + lim →2 () [Limit Law 1] = −1 + 2 = 1 (b) lim →0 () exists, but lim →0 () does not exist, so we cannot apply Limit Law 2 to lim →0 [() − ()]. The limit does not exist. (c) lim →−1 [() ()] = lim →−1 () · lim →−1 () [Limit Law 4] = 1 · 2 = 2 (d) lim →3 () = 1, but lim →3 () = 0, so we cannot apply Limit Law 5 to lim →3 () () . The limit does not exist. Note: lim →3− () () = ∞ since () → 0+ as → 3− and lim →3+ (()) = −∞ since () → 0−as → 3+. Therefore, the limit does not exist, even as an infinite limit. (e) lim →2 2() = lim →2 2 · lim →2 () [Limit Law 4] = 22 · (−1) = −4 (f) (−1) + lim →−1 () is undefined since (−1) is not defined. 3. lim →3 (53 − 32 + − 6) = lim →3 (53) − lim →3 (32) + lim →3 − lim →3 6 [Limit Laws 2 and 1] = 5 lim →3 3 − 3 lim →3 2 + lim →3 − lim →3 6 [3] = 5(33) − 3(32) + 3 − 6 [9, 8, and 7] = 105 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS ¤ 81 4. lim →−1 (4 − 3)(2 + 5 + 3) = lim →−1 (4 − 3) lim →−1 (2 + 5 + 3) [Limit Law 4] = lim →−1 4 − lim →−1 3lim →−1 2 + lim →−1 5 + lim →−1 3 [2, 1] = lim →−1 4 − 3 lim →−1 lim →−1 2 + 5 lim →−1 + lim →−1 3 [3] = (1 + 3)(1 − 5 + 3) [9, 8, and 7] = 4(−1) = −4 5. lim →−2 4 − 2 22 − 3 + 2 = lim →−2 (4 − 2) lim →−2 (22 − 3 + 2) [Limit Law 5] = lim →−2 4 − lim →−2 2 2 lim →−2 2 − 3 lim →−2 + lim →−2 2 [1, 2, and 3] = 16 − 2 2(4) − 3(−2) + 2 [9, 7, and 8] = 14 16 = 7 8 6. lim →−2 √4 + 3 + 6 = lim →−2 (4 + 3 + 6) [11] = lim →−2 4 + 3 lim →−2 + lim →−2 6 [1, 2, and 3] = (−2)4 + 3 (−2) + 6 [9, 8, and 7] = √16 − 6 + 6 = √16 = 4 7. lim →8 (1 + √3 ) (2 − 62 + 3) = lim →8 (1 + √3 ) · lim →8 (2 − 62 + 3) [Limit Law 4] = lim →8 1 + lim →8 √3 · lim →8 2 − 6 lim →8 2 + lim →8 3 [1, 2, and 3] = 1 + √3 8 · 2 − 6 · 82 + 83 [7, 10, 9] = (3)(130) = 390 8. lim →23 −2 3− 2+ 52 = lim →2 3 −2 3− 2+ 52 [Limit Law 6] = lim →2 (2 − 2) lim →2 (3 − 3 + 5) 2 [5] = lim →2 2 − lim →2 2 lim →2 3 − 3 lim →2 + lim →2 5 2 [1, 2, and 3] = 8 −43(2) + 5 − 2 2 [9, 7, and 8] = 722 = 49 4 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.82 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 9. lim →2 232−+ 1 2 = lim →2 232−+ 1 2 [Limit Law 11] = lim →2 (22 + 1) lim →2 (3 − 2) [5] = 2 lim →2 2 + lim →2 1 3 lim →2 − lim →2 2 [1, 2, and 3] = 2(2) 3(2)2−+ 1 2 = 9 4 = 32 [9, 8, and 7] 10. (a) The left-hand side of the equation is not defined for = 2, but the right-hand side is. (b) Since the equation holds for all 6= 2, it follows that both sides of the equation approach the same limit as → 2, just as in Example 3. Remember that in finding lim → (), we never consider = . 11. lim →5 2 − 6 + 5 − 5 = lim →5 ( − 5)( − 1) − 5 = lim →5 ( − 1) = 5 − 1 = 4 12. lim →−3 2 + 3 2 − − 12 = lim →−3 ( −(4)( + 3) + 3) = lim →−3 − 4 = −3−−3 4 = 37 13. lim →5 2 − 5 + 6 − 5 does not exist since − 5 → 0, but 2 − 5 + 6 → 6 as → 5. 14. lim →4 2 + 3 2 − − 12 = lim →4 ( −(4)( + 3) + 3) = lim →4 − 4. The last limit does not exist since lim →4− − 4 = −∞ and lim →4+ − 4 = ∞. 15. lim →−3 2 − 9 22 + 7 + 3 = lim →−3 (2 (+ 3)( + 1)(−+ 3) 3) = lim →−3 2−+ 1 3 = 2(−−33) + 1 − 3 = −−65 = 65 16. lim →−1 22 + 3 + 1 2 − 2 − 3 = lim →−1 (2 (−+ 1)( 3)(+ 1) + 1) = lim →−1 2−+ 1 3 = 2(−−11) + 1 − 3 = −−14 = 14 17. lim →0 (−5 + )2 − 25 = lim →0 (25 − 10+ 2) − 25 = lim →0 −10+ 2 = lim →0 (−10 + ) = lim →0(−10 + ) = −10 18. lim →0 (2 + )3 − 8 = lim →0 8 + 12 + 62 + 3 − 8 = lim →0 12 + 62 + 3 = lim →0 12 + 6 + 2 = 12 + 0 + 0 = 12 19. By the formula for the sum of cubes, we have lim →−2 + 2 3 + 8 = lim →−2 ( + 2)(2+ 2 − 2 + 4) = lim →−2 2 − 21 + 4 = 4 + 4 + 4 1 = 12 1 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS ¤ 83 20. We use the difference of squares in the numerator and the difference of cubes in the denominator. lim →1 4 − 1 3 − 1 = lim →1 ((−2 1)( − 1)( 2 +2 + 1) + 1) = lim →1 ((− −1)( 1)( + 1)( 2 + 2+ 1) + 1) = lim →1 ( + 1)( 2 + 2+ 1 + 1) = 2(2) 3 = 43 21. lim →0 √9 + − 3 = lim →0 √9 + − 3 · √9 + + 3 √9 + + 3 = lim →0 √9 + 2 − 32 √9 + + 3 = lim →0 (9 + √9 +)−+ 3 9 = lim →0 √9 + + 3 = lim →0 √9 +1 + 3 = 3 + 3 1 = 1 6 22. lim →2 √4 + 1 − 3 − 2 = lim →2 √4 + 1 − 3 − 2 · √4 + 1 + 3 √4 + 1 + 3 = lim →2 √4 + 1 2 − 32 ( − 2)√4 + 1 + 3 = lim →2 4 + 1 − 9 ( − 2)√4 + 1 + 3 = lim →2 ( − 2)4( √4−2) + 1 + 3 = lim →2 4 √4 + 1 + 3 = 4 √9 + 3 = 2 3 23. lim →3 1 − 1 3 − 3 = lim →3 1 − 1 3 − 3 · 3 3 = lim →3 3 − 3( − 3) = lim →3 −31 = −19 24. lim →0 (3 + )−1 − 3−1 = lim →0 1 3 + − 1 3 = lim →0 3−(3 + (3 +)3 ) = lim →0 (3 + −)3 = lim →0 −3(3 + 1 ) = − lim 1 →0 [3(3 + )] = − 1 3(3 + 0) = − 1 9 25. lim →0 √1 + − √1 − = lim →0 √1 + − √1 − · √1 + + √1 − √1 + + √1 − = lim →0 √1 + 2 − √1 − 2 √1 + + √1 − = lim →0 (1 + ) − (1 − ) √1 + + √1 − = lim →0 √1 + 2+ √1 − = lim →0 √1 + +2 √1 − = 2 √1 + √1 = 2 2 = 1 26. lim →0 1 − 2 1+ = lim →0 1 − ( + 1) 1 = lim →0 + 1 ( + 1) − 1 = lim →0 + 1 1 = 0 + 1 1 = 1 27. lim →16 4 − √ 16 − 2 = lim →16 (16 (4 − −√2)(4 + )(4 +√√)) = lim →16 (16 −16 )(4 + − √ ) = lim →16 1 (4 + √ ) = 1 16 4 + √16 = 1 16(8) = 1 128 28. lim →2 2 − 4 + 4 4 − 32 − 4 = lim →2 (2 −(4)( − 2)22+ 1) = lim →2 ( + 2)( ( − − 2) 2)(22 + 1) = lim →2 − 2 ( + 2)(2 + 1) = 0 4 · 5 = 0 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.84 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 29. lim →0 √1 + 1 − 1 = lim →0 1−√√1 + 1 + = lim →0 1−√√ + 1 1 +1 + 1 + √1 + √1 + = lim →0 √1 + 1 + − √1 + = lim →0 −1 √1 + 1 + √1 + = −1 √1 + 0 1 + √1 + 0 = − 1 2 30. lim →−4 √2 + 9 − 5 + 4 = lim →−4 √2 + 9 − 5√2 + 9 + 5 ( + 4)√2 + 9 + 5 = lim →−4 ( + 4) (2+ 9) √2 −+ 9 + 5 25 = lim →−4 2 − 16 ( + 4)√2 + 9 + 5 = lim →−4 ( + 4) ( + 4)( √2+ 9 + 5 − 4) = lim →−4 − 4 √2 + 9 + 5 = −4 − 4 √16 + 9 + 5 = −8 5 + 5 = − 4 5 31. lim →0 ( + )3 − 3 = lim →0 (3 + 32 + 32 + 3) − 3 = lim →0 32 + 32 + 3 = lim →0 (32 + 3 + 2) = lim →0(32 + 3 + 2) = 32 32. lim →0 1 ( + )2 − 1 2 = lim →0 2 − ( + )2 ( + )22 = lim →0 2 − (22(+ 2 + )2+ 2) = lim →0 −2(2 (++))2 = lim →0 −(2 + ) 2( + )2 = −2 2 · 2 = − 2 3 33. (a) lim →0 √1 + 3 − 1 ≈ 2 3 (b) () −0001 0666 166 3 −0000 1 0666 616 7 −0000 01 0666 661 7 −0000 001 0666 666 2 0000 001 0666 667 2 0000 01 0666 671 7 0000 1 0666 716 7 0001 0667 166 3 The limit appears to be 2 3 . (c) lim →0 √1 + 3 − 1 · √√1 + 3 1 + 3 + 1 + 1 = lim →0 (1 + 3 √1 + 3 )−+ 1 1 = lim →0 √1 + 3 3 + 1 = 1 3 lim →0 √1 + 3 + 1 [Limit Law 3] = 1 3 lim →0(1 + 3) + lim →0 1 [1 and 11] = 1 3 lim →0 1 + 3 lim →0 + 1 [1, 3, and 7] = 1 3 √1 + 3 · 0 + 1 [7 and 8] = 1 3 (1 + 1) = 2 3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS ¤ 85 34. (a) lim →0 √3 + − √3 ≈ 029 (b) () −0001 0288 699 2 −0000 1 0288 677 5 −0000 01 0288 675 4 −0000 001 0288 675 2 0000 001 0288 675 1 0000 01 0288 674 9 0000 1 0288 672 7 0001 0288 651 1 The limit appears to be approximately 02887. (c) lim →0 √3 + − √3 · √√3 + 3 + + + √ √3 3 = lim →0 √(3 + 3 +)+−√3 3 = lim →0 √3 + 1 + √3 = lim →0 1 lim →0 √3 + + lim →0 √3 [Limit Laws 5 and 1] = 1 lim →0 (3 + ) + √3 [7 and 11] = 1 √3 + 0 + √3 [1, 7, and 8] = 1 2 √3 35. Let () = −2, () = 2 cos 20 and () = 2. Then −1 ≤ cos 20 ≤ 1 ⇒ −2 ≤ 2 cos 20 ≤ 2 ⇒ () ≤ () ≤ (). So since lim →0 () = lim →0 () = 0, by the Squeeze Theorem we have lim →0 () = 0. 36. Let () = −√3 + 2, () = √3 + 2 sin(), and () = √3 + 2. Then −1 ≤ sin() ≤ 1 ⇒ −√3 + 2 ≤ √3 + 2 sin() ≤ √3 + 2 ⇒ () ≤ () ≤ (). So since lim →0 () = lim →0 () = 0, by the Squeeze Theorem we have lim →0 () = 0. 37. We have lim →4 (4 − 9) = 4(4) − 9 = 7 and lim →4 2 − 4 + 7 = 42 − 4(4) + 7 = 7. Since 4 − 9 ≤ () ≤ 2 − 4 + 7 for ≥ 0, lim →4 () = 7 by the Squeeze Theorem. 38. We have lim →1 (2) = 2(1) = 2 and lim →1 (4 − 2 + 2) = 14 − 12 + 2 = 2. Since 2 ≤ () ≤ 4 − 2 + 2 for all , lim →1 () = 2 by the Squeeze Theorem. 39. −1 ≤ cos(2) ≤ 1 ⇒ −4 ≤ 4 cos(2) ≤ 4. Since lim →0 −4 = 0 and lim →0 4 = 0, we have lim →0 4 cos(2) = 0 by the Squeeze Theorem. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.86 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 40. −1 ≤ sin() ≤ 1 ⇒ −1 ≤ sin() ≤ 1 ⇒ √/ ≤ √ sin() ≤ √ . Since lim →0+ (√/) = 0 and lim →0+ (√ ) = 0, we have lim →0+ √ sin() = 0 by the Squeeze Theorem. 41. | − 3| = − (−3− 3) if if − − 3 3 ≥ 0 0 = 3 −−3 if if ≥ 33 Thus, lim →3+ (2 + | − 3|) = lim →3+ (2 + − 3) = lim →3+ (3 − 3) = 3(3) − 3 = 6 and lim →3− (2 + | − 3|) = lim →3− (2 + 3 − ) = lim →3− ( + 3) = 3 + 3 = 6. Since the left and right limits are equal, lim →3 (2 + | − 3|) = 6. 42. | + 6| = − (+ 6 + 6) if if + 6 + 6 ≥ 0 0 = −(+ 6 + 6) if if ≥ −−66 We’ll look at the one-sided limits. lim →−6+ 2 + 12 | + 6| = lim →−6+ 2(+ 6 + 6) = 2 and →− lim6− 2| + 12 + 6| = lim →−6− −2((+ 6) + 6) = −2 The left and right limits are different, so lim →−6 2 + 12 | + 6| does not exist. 43. 23 − 2 = 2(2 − 1) = 2 · |2 − 1| = 2 |2 − 1| |2 − 1| = −2(2−1− 1) if if 2 2 − − 1 1 ≥ 0 0 = 2 −(2−1− 1) if if ≥ 0055 So 23 − 2 = 2[−(2 − 1)] for 05. Thus, lim →05− 2 − 1 |23 − 2| = lim →05− 2[−2(2− −1 1)] = lim →05− −21 = (0−5) 1 2 = 0−25 1 = −4. 44. Since || = − for 0, we have lim →−2 2 − || 2 + = lim →−2 2 − (−) 2 + = lim →−2 2 + 2 + = lim →−2 1 = 1. 45. Since || = − for 0, we have lim →0− 1 − |1| = lim →0− 1 − −1 = lim →0− 2 , which does not exist since the denominator approaches 0 and the numerator does not. 46. Since || = for 0, we have lim →0+ 1 − |1| = lim →0+ 1 − 1 = lim →0+ 0 = 0. 47. (a) (b) (i) Since sgn = 1 for 0, lim →0+ sgn = lim →0+ 1 = 1. (ii) Since sgn = −1 for 0, lim →0− sgn = lim →0− −1 = −1. (iii) Since lim →0− sgn 6= lim →0+ sgn , lim →0 sgn does not exist. (iv) Since |sgn | = 1 for 6= 0, lim →0 |sgn | = lim →0 1 = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS ¤ 87 48. (a) () = sgn(sin ) = −1 if sin 0 0 if sin = 0 1 if sin 0 (i) lim →0+ () = lim →0+ sgn(sin ) = 1 since sin is positive for small positive values of . (ii) lim →0− () = lim →0− sgn(sin ) = −1 since sin is negative for small negative values of . (iii) lim →0 () does not exist since lim →0+ () 6= lim →0− (). (iv) lim →+ () = lim →+ sgn(sin ) = −1 since sin is negative for values of slightly greater than . (v) lim →− () = lim →− sgn(sin ) = 1 since sin is positive for values of slightly less than . (vi) lim → () does not exist since lim →+ () 6= lim →− (). (b) The sine function changes sign at every integer multiple of , so the signum function equals 1 on one side and −1 on the other side of , an integer. Thus, lim → () does not exist for = , an integer. (c) 49. (a) (i) lim →2+ () = lim →2+ 2 + − 6 | − 2| = lim →2+ ( + 3)( | −2|− 2) = lim →2+ ( + 3)( − 2) − 2 [since − 2 0 if → 2+] = lim →2+ ( + 3) = 5 (ii) The solution is similar to the solution in part (i), but now | − 2| = 2 − since − 2 0 if → 2−. Thus, lim →2− () = lim →2− −( + 3) = −5. (b) Since the right-hand and left-hand limits of at = 2 are not equal, lim →2 () does not exist. (c) 50. (a) () =(2 −+ 1 2)2 if if ≥ 1 1 lim →1− () = lim →1− (2 + 1) = 12 + 1 = 2, lim →1+ () = lim →1+ ( − 2)2 = (−1)2 = 1 (b) Since the right-hand and left-hand limits of at = 1 are not equal, lim →1 () does not exist. (c) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.88 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 51. For the lim →2 () to exist, the one-sided limits at = 2 must be equal. lim →2− () = lim →2− 4 − 1 2 = 4 − 1 = 3 and lim →2+ () = lim →2+ √ + = √2 + . Now 3 = √2 + ⇒ 9 = 2 + ⇔ = 7. 52. (a) (i) lim →1− () = lim →1− = 1 (ii) lim →1+ () = lim →1+ (2 − 2) = 2 − 12 = 1. Since lim →1− () = 1 and lim →1+ () = 1, we have lim →1 () = 1. Note that the fact (1) = 3 does not affect the value of the limit. (iii) When = 1, () = 3, so (1) = 3. (iv) lim →2− () = lim →2− (2 − 2) = 2 − 22 = 2 − 4 = −2 (v) lim →2+ () = lim →2+ ( − 3) = 2 − 3 = −1 (vi) lim →2 () does not exist since lim →2− () 6= lim →2+ (). (b) () = if 1 3 if = 1 2 − 2 if 1 ≤ 2 − 3 if 2 53. (a) (i) [[]] = −2 for −2 ≤ −1, so lim →−2+ [[]] = lim →−2+ (−2) = −2 (ii) [[]] = −3 for −3 ≤ −2, so lim →−2− [[]] = lim →−2− (−3) = −3. The right and left limits are different, so lim →−2 [[]] does not exist. (iii) [[]] = −3 for −3 ≤ −2, so lim →−24 [[]] = lim →−24 (−3) = −3. (b) (i) [[]] = − 1 for − 1 ≤ , so lim →− [[]] = lim →− ( − 1) = − 1. (ii) [[]] = for ≤ + 1, so lim →+ [[]] = lim →+ = . (c) lim → [[]] exists ⇔ is not an integer. 54. (a) See the graph of = cos . Since −1 ≤ cos 0 on [− −2), we have = () = [[cos ]] = −1 on [− −2). Since 0 ≤ cos 1 on [−2 0) ∪ (0 2], we have () = 0 on [−2 0) ∪ (0 2]. Since −1 ≤ cos 0 on (2 ], we have () = −1 on (2 ]. Note that (0) = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS ¤ 89 (b) (i) lim →0− () = 0 and lim →0+ () = 0, so lim →0 () = 0. (ii) As → (2)−, () → 0, so lim →(2)− () = 0. (iii) As → (2)+, () → −1, so lim →(2)+ () = −1. (iv) Since the answers in parts (ii) and (iii) are not equal, lim →2 () does not exist. (c) lim → () exists for all in the open interval (− ) except = −2 and = 2. 55. The graph of () = [[]] + [[−]] is the same as the graph of () = −1 with holes at each integer, since () = 0 for any integer . Thus, lim →2− () = −1 and lim →2+ () = −1, so lim →2 () = −1. However, (2) = [[2]] + [[−2]] = 2 + (−2) = 0, so lim →2 () 6= (2). 56. lim →− 01 − 22 = 0√1 − 1 = 0. As the velocity approaches the speed of light, the length approaches 0. A left-hand limit is necessary since is not defined for . 57. Since () is a polynomial, () = 0 + 1 + 22 + · · · + . Thus, by the Limit Laws, lim → () = lim → 0 + 1 + 22 + · · · + = 0 + 1 lim → + 2 lim → 2 + · · · + lim → = 0 + 1 + 22 + · · · + = () Thus, for any polynomial , lim → () = (). 58. Let () = () () where () and () are any polynomials, and suppose that () 6= 0. Then lim → () = lim → () () = lim → () lim → () [Limit Law 5] = (()) [Exercise 57] = (). 59. lim →1 [() − 8] = lim →1 (−) −1 8 · ( − 1) = lim →1 (−) −1 8 · lim →1( − 1) = 10 · 0 = 0. Thus, lim →1 () = lim →1 {[() − 8] + 8} = lim →1 [() − 8] + lim →1 8 = 0 + 8 = 8. Note: The value of lim →1 () − 8 − 1 does not affect the answer since it’s multiplied by 0. What’s important is that lim →1 () − 8 − 1 exists. 60. (a) lim →0 () = lim →0 (2) · 2 = lim →0 (2) · lim →0 2 = 5 · 0 = 0 (b) lim →0 () = lim →0 (2) · = lim →0 (2) · lim →0 = 5 · 0 = 0 61. Observe that 0 ≤ () ≤ 2 for all , and lim →0 0 = 0 = lim →0 2. So, by the Squeeze Theorem, lim →0 () = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.90 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 62. Let () = [[]] and () = −[[]]. Then lim →3 () and lim →3 () do not exist [Example 10] but lim →3 [() + ()] = lim →3 ([[]] − [[]]) = lim →3 0 = 0. 63. Let () = () and () = 1 − (), where is the Heaviside function defined in Exercise 1.3.59. Thus, either or is 0 for any value of . Then lim →0 () and lim →0 () do not exist, but lim →0 [()()] = lim →0 0 = 0. 64. lim →2 √6 − − 2 √3 − − 1 = lim →2 √ √6 3 − − − − 2 1 · √√6 6 − − + 2 + 2 · √√3 3 − − + 1 + 1 = lim →2 √√6 3 − − 2 2 − − 2 12 2 · √√3 6 − − + 1 + 2 = lim →2 6 3 − − − − 4 1 · √√3 6 − − + 1 + 2 = lim →2 (2 − )√3 − + 1 (2 − )√6 − + 2 = lim →2 √3 − + 1 √6 − + 2 = 1 2 65. Since the denominator approaches 0 as → −2, the limit will exist only if the numerator also approaches 0 as → −2. In order for this to happen, we need lim →−2 32 + + + 3 = 0 ⇔ 3(−2)2 + (−2) + + 3 = 0 ⇔ 12 − 2 + + 3 = 0 ⇔ = 15. With = 15, the limit becomes lim →−2 32 + 15 + 18 2 + − 2 = lim →−2 3( (−+ 2)( 1)(+ 2) + 3) = lim →−2 3(−+ 3) 1 = 3(−−22 + 3) − 1 = −33 = −1. 66. Solution 1: First, we find the coordinates of and as functions of . Then we can find the equation of the line determined by these two points, and thus find the -intercept (the point ), and take the limit as → 0. The coordinates of are (0 ). The point is the point of intersection of the two circles 2 + 2 = 2 and ( − 1)2 + 2 = 1. Eliminating from these equations, we get 2 − 2 = 1 − ( − 1)2 ⇔ 2 = 1 + 2 − 1 ⇔ = 1 22. Substituting back into the equation of the shrinking circle to find the -coordinate, we get 1 222 + 2 = 2 ⇔ 2 = 21 − 1 42 ⇔ = 1 − 1 42 (the positive -value). So the coordinates of are 1 22 1 − 1 42 . The equation of the line joining and is thus − = 1 − 1 42 − 12 2 − 0 ( − 0). We set = 0 in order to find the -intercept, and get = − 12 2 1 − 1 42 − 1 = − 12 2 1 − 1 42 + 1 1 − 1 42 − 1 = 2 1 − 1 42 + 1 Now we take the limit as → 0+: lim →0+ = lim →0+ 21 − 1 42 + 1= lim →0+ 2 √1 + 1 = 4. So the limiting position of is the point (4 0). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.4 THE PRECISE DEFINITION OF A LIMIT ¤ 91 Solution 2: We add a few lines to the diagram, as shown. Note that ∠ = 90◦ (subtended by diameter ). So ∠ = 90◦ = ∠ (subtended by diameter ). It follows that ∠ = ∠ . Also ∠ = 90◦ − ∠ = ∠ . Since 4 is isosceles, so is 4, implying that = . As the circle 2 shrinks, the point plainly approaches the origin, so the point must approach a point twice as far from the origin as , that is, the point (4 0), as above. 2.4 The Precise Definition of a Limit 1. If |() − 1| 02, then −02 () − 1 02 ⇒ 08 () 12. From the graph, we see that the last inequality is true if 07 11, so we can choose = min {1 − 07 11 − 1} = min {03 01} = 01 (or any smaller positive number). 2. If |() − 2| 05, then −05 () − 2 05 ⇒ 15 () 25. From the graph, we see that the last inequality is true if 26 38, so we can take = min {3 − 26 38 − 3} = min {04 08} = 04 (or any smaller positive number). Note that 6= 3. 3. The leftmost question mark is the solution of √ = 16 and the rightmost, √ = 24. So the values are 162 = 256 and 242 = 576. On the left side, we need | − 4| |256 − 4| = 144. On the right side, we need | − 4| |576 − 4| = 176. To satisfy both conditions, we need the more restrictive condition to hold— namely, | − 4| 144. Thus, we can choose = 144, or any smaller positive number. 4. The leftmost question mark is the positive solution of 2 = 1 2, that is, = √12, and the rightmost question mark is the positive solution of 2 = 3 2, that is, = 3 2. On the left side, we need | − 1| √12 − 1 ≈ 0292 (rounding down to be safe). On the right side, we need | − 1| 3 2 − 1 ≈ 0224. The more restrictive of these two conditions must apply, so we choose = 0224 (or any smaller positive number). 5. From the graph, we find that = tan = 08 when ≈ 0675, so 4 − 1 ≈ 0675 ⇒ 1 ≈ 4 − 0675 ≈ 01106. Also, = tan = 12 when ≈ 0876, so 4 + 2 ≈ 0876 ⇒ 2 = 0876 − 4 ≈ 00906. Thus, we choose = 00906 (or any smaller positive number) since this is the smaller of 1 and 2. 6. From the graph, we find that = 2(2 + 4) = 03 when = 2 3, so 1 − 1 = 2 3 ⇒ 1 = 1 3. Also, = 2(2 + 4) = 05 when = 2, so 1 + 2 = 2 ⇒ 2 = 1. Thus, we choose = 1 3 (or any smaller positive number) since this is the smaller of 1 and 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.92 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 7. From the graph with = 02, we find that = 3 − 3 + 4 = 58 when ≈ 19774, so 2 − 1 ≈ 19774 ⇒ 1 ≈ 00226. Also, = 3 − 3 + 4 = 62 when ≈ 2022, so 2 + 2 ≈ 20219 ⇒ 2 ≈ 00219. Thus, we choose = 00219 (or any smaller positive number) since this is the smaller of 1 and 2. For = 01, we get 1 ≈ 00112 and 2 ≈ 00110, so we choose = 0011 (or any smaller positive number). 8. From the graph with = 05, we find that = (2 − 1) = 15 when ≈ −0303, so 1 ≈ 0303. Also, = (2 − 1) = 25 when ≈ 0215, so 2 ≈ 0215. Thus, we choose = 0215 (or any smaller positive number) since this is the smaller of 1 and 2. For = 01, we get 1 ≈ 0052 and 2 ≈ 0048, so we choose = 0048 (or any smaller positive number). 9. (a) The first graph of = 1 ln( − 1) shows a vertical asymptote at = 2. The second graph shows that = 100 when ≈ 201 (more accurately, 201005). Thus, we choose = 001 (or any smaller positive number). (b) From part (a), we see that as gets closer to 2 from the right, increases without bound. In symbols, lim →2+ 1 ln( − 1) = ∞. 10. We graph = csc2 and = 500. The graphs intersect at ≈ 3186, so we choose = 3186 − ≈ 0044. Thus, if 0 | − | 0044, then csc2 500. Similarly, for = 1000, we get = 3173 − ≈ 0031. 11. (a) = 2 and = 1000 cm2 ⇒ 2 = 1000 ⇒ 2 = 1000 ⇒ = 1000 ( 0) ≈ 178412 cm. (b) | − 1000| ≤ 5 ⇒ −5 ≤ 2 − 1000 ≤ 5 ⇒ 1000 − 5 ≤ 2 ≤ 1000 + 5 ⇒ 995 ≤ ≤ 1005 ⇒ 177966 ≤ ≤ 178858. 1000 − 995 ≈ 004466 and 1005 − 1000 ≈ 004455. So if the machinist gets the radius within 00445 cm of 178412, the area will be within 5 cm2 of 1000. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.4 THE PRECISE DEFINITION OF A LIMIT ¤ 93 (c) is the radius, () is the area, is the target radius given in part (a), is the target area (1000), is the tolerance in the area (5), and is the tolerance in the radius given in part (b). 12. (a) = 012 + 2155 + 20 and = 200 ⇒ 012 + 2155 + 20 = 200 ⇒ [by the quadratic formula or from the graph] ≈ 330 watts ( 0) (b) From the graph, 199 ≤ ≤ 201 ⇒ 3289 3311. (c) is the input power, () is the temperature, is the target input power given in part (a), is the target temperature (200), is the tolerance in the temperature (1), and is the tolerance in the power input in watts indicated in part (b) (011 watts). 13. (a) |4 − 8| = 4 | − 2| 01 ⇔ | − 2| 01 4 , so = 041 = 0025. (b) |4 − 8| = 4 | − 2| 001 ⇔ | − 2| 001 4 , so = 0401 = 00025. 14. |(5 − 7) − 3| = |5 − 10| = |5( − 2)| = 5 | − 2|. We must have |() − | , so 5 | − 2| ⇔ | − 2| 5. Thus, choose = 5. For = 01, = 002; for = 005, = 001; for = 001, = 0002. 15. Given 0, we need 0 such that if 0 | − 3| , then (1 + 1 3) − 2 . But (1 + 1 3) − 2 ⇔ 1 3 − 1 ⇔ 13 | − 3| ⇔ | − 3| 3. So if we choose = 3, then 0 | − 3| ⇒ (1 + 1 3) − 2 . Thus, lim →3 (1 + 1 3) = 2 by the definition of a limit. 16. Given 0, we need 0 such that if 0 | − 4| , then |(2 − 5) − 3| . But |(2 − 5) − 3| ⇔ |2 − 8| ⇔ |2| | − 4| ⇔ | − 4| 2. So if we choose = 2, then 0 | − 4| ⇒ |(2 − 5) − 3| . Thus, lim →4 (2 − 5) = 3 by the definition of a limit. 17. Given 0, we need 0 such that if 0 | − (−3)| , then |(1 − 4) − 13| . But |(1 − 4) − 13| ⇔ |−4 − 12| ⇔ |−4| | + 3| ⇔ | − (−3)| 4. So if we choose = 4, then 0 | − (−3)| ⇒ |(1 − 4) − 13| . Thus, lim →−3 (1 − 4) = 13 by the definition of a limit. x °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.94 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 18. Given 0, we need 0 such that if 0 | − (−2)| , then |(3 + 5) − (−1)| . But |(3 + 5) − (−1)| ⇔ |3 + 6| ⇔ |3| | + 2| ⇔ | + 2| 3. So if we choose = 3, then 0 | + 2| ⇒ |(3 + 5) − (−1)| . Thus, lim →−2 (3 + 5) = −1 by the definition of a limit. 19. Given 0, we need 0 such that if 0 | − 1| , then 2 + 4 3 − 2 . But 2 + 4 3 − 2 ⇔ 4 − 4 3 ⇔ 4 3 | − 1| ⇔ | − 1| 3 4. So if we choose = 3 4, then 0 | − 1| ⇒ 2 + 4 3 − 2 . Thus, lim →1 2 + 4 3 = 2 by the definition of a limit. 20. Given 0, we need 0 such that if 0 | − 10| , then 3 − 4 5 − (−5) . But 3 − 4 5 − (−5) ⇔ 8 − 4 5 ⇔ − 4 5 | − 10| ⇔ | − 10| 5 4. So if we choose = 5 4, then 0 | − 10| ⇒ 3 − 4 5 − (−5) . Thus, lim →10 (3 − 4 5) = −5 by the definition of a limit. 21. Given 0, we need 0 such that if 0 | − 4| , then 2 − 2 − 8 − 4 − 6 ⇔ ( − 4)( + 2) − 4 − 6 ⇔ | + 2 − 6| [ 6= 4] ⇔ | − 4| . So choose = . Then 0 | − 4| ⇒ | − 4| ⇒ | + 2 − 6| ⇒ ( − 4)( + 2) − 4 − 6 [ 6= 4] ⇒ 2 − 2 − 8 − 4 − 6 . By the definition of a limit, lim →4 2 − 2 − 8 − 4 = 6. 22. Given 0, we need 0 such that if 0 | + 15| , then 9 − 42 3 + 2 − 6 ⇔ (3 + 2)(3 − 2) 3 + 2 − 6 ⇔ |3 − 2 − 6| [ 6= −15] ⇔ |−2 − 3| ⇔ |−2| | + 15| ⇔ | + 15| 2. So choose = 2. Then 0 | + 15| ⇒ | + 15| 2 ⇒ |−2| | + 15| ⇒ |−2 − 3| ⇒ |3 − 2 − 6| ⇒ (3 + 2)(3 − 2) 3 + 2 − 6 [ 6= −15] ⇒ 9 − 42 3 + 2 − 6 . By the definition of a limit, lim →−15 9 − 42 3 + 2 = 6. 23. Given 0, we need 0 such that if 0 | − | , then | − | . So = will work. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.4 THE PRECISE DEFINITION OF A LIMIT ¤ 95 24. Given 0, we need 0 such that if 0 | − | , then | − | . But | − | = 0, so this will be true no matter what we pick. 25. Given 0, we need 0 such that if 0 | − 0| , then 2 − 0 ⇔ 2 ⇔ || √. Take = √. Then 0 | − 0| ⇒ 2 − 0 . Thus, lim →0 2 = 0 by the definition of a limit. 26. Given 0, we need 0 such that if 0 | − 0| , then 3 − 0 ⇔ ||3 ⇔ || √3 . Take = √3 . Then 0 | − 0| ⇒ 3 − 0 3 = . Thus, lim →0 3 = 0 by the definition of a limit. 27. Given 0, we need 0 such that if 0 | − 0| , then || − 0 . But || = ||. So this is true if we pick = . Thus, lim →0 || = 0 by the definition of a limit. 28. Given 0, we need 0 such that if 0 − (−6) , then √8 6 + − 0 . But √8 6 + − 0 ⇔ √8 6 + ⇔ 6 + 8 ⇔ − (−6) 8. So if we choose = 8, then 0 − (−6) ⇒ √8 6 + − 0 . Thus, lim →−6+ √8 6 + = 0 by the definition of a right-hand limit. 29. Given 0, we need 0 such that if 0 | − 2| , then 2 − 4 + 5 − 1 ⇔ 2 − 4 + 4 ⇔ ( − 2)2 . So take = √. Then 0 | − 2| ⇔ | − 2| √ ⇔ ( − 2)2 . Thus, lim →2 2 − 4 + 5 = 1 by the definition of a limit. 30. Given 0, we need 0 such that if 0 | − 2| , then (2 + 2 − 7) − 1 . But (2 + 2 − 7) − 1 ⇔ 2 + 2 − 8 ⇔ | + 4| | − 2| . Thus our goal is to make | − 2| small enough so that its product with | + 4| is less than . Suppose we first require that | − 2| 1. Then −1 − 2 1 ⇒ 1 3 ⇒ 5 + 4 7 ⇒ | + 4| 7, and this gives us 7 | − 2| ⇒ | − 2| 7. Choose = min {1 7}. Then if 0 | − 2| , we have | − 2| 7 and | + 4| 7, so (2 + 2 − 7) − 1 = |( + 4)( − 2)| = | + 4| | − 2| 7(7) = , as desired. Thus, lim →2 (2 + 2 − 7) = 1 by the definition of a limit. 31. Given 0, we need 0 such that if 0 | − (−2)| , then 2 − 1 − 3 or upon simplifying we need 2 − 4 whenever 0 | + 2| . Notice that if | + 2| 1, then −1 + 2 1 ⇒ −5 − 2 −3 ⇒ | − 2| 5. So take = min {5 1}. Then 0 | + 2| ⇒ | − 2| 5 and | + 2| 5, so 2 − 1 − 3 = |( + 2)( − 2)| = | + 2| | − 2| (5)(5) = . Thus, by the definition of a limit, lim →−2 (2 − 1) = 3. 32. Given 0, we need 0 such that if 0 | − 2| , then 3 − 8 . Now 3 − 8 = ( − 2)2 + 2 + 4 . If | − 2| 1, that is, 1 3, then 2 + 2 + 4 32 + 2(3) + 4 = 19 and so 3 − 8 = | − 2| 2 + 2 + 4 19 | − 2|. So if we take = min 1 19 , then 0 | − 2| ⇒ 3 − 8 = | − 2| 2 + 2 + 4 19 · 19 = . Thus, by the definition of a limit, lim →2 3 = 8. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.96 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 33. Given 0, we let = min 2 8. If 0 | − 3| , then | − 3| 2 ⇒ −2 − 3 2 ⇒ 4 + 3 8 ⇒ | + 3| 8. Also | − 3| 8 , so 2 − 9 = | + 3| | − 3| 8 · 8 = . Thus, lim →3 2 = 9. 34. From the figure, our choices for are 1 = 3 − √9 − and 2 = √9 + − 3. The largest possible choice for is the minimum value of {1 2}; that is, = min{1 2} = 2 = √9 + − 3. 35. (a) The points of intersection in the graph are (1 26) and (2 34) with 1 ≈ 0891 and 2 ≈ 1093. Thus, we can take to be the smaller of 1 − 1 and 2 − 1. So = 2 − 1 ≈ 0093. (b) Solving 3 + + 1 = 3 + gives us two nonreal complex roots and one real root, which is () = 216 + 108 + 12√336 + 324 + 812 23 − 12 6216 + 108 + 12√336 + 324 + 812 13 . Thus, = () − 1. (c) If = 04, then () ≈ 1093 272 342 and = () − 1 ≈ 0093, which agrees with our answer in part (a). 36. 1. Guessing a value for Let 0 be given. We have to find a number 0 such that 1 − 1 2 whenever 0 | − 2| . But 1 − 1 2 = 2 − 2 = | − 2| |2| . We find a positive constant such that |21| ⇒ | − 2| |2| | − 2| and we can make | − 2| by taking | − 2| = . We restrict to lie in the interval | − 2| 1 ⇒ 1 3 so 1 1 1 3 ⇒ 1 6 1 2 1 2 ⇒ 1 |2| 1 2 . So = 1 2 is suitable. Thus, we should choose = min {1 2}. 2. Showing that works Given 0 we let = min {1 2}. If 0 | − 2| , then | − 2| 1 ⇒ 1 3 ⇒ 1 |2| 1 2 (as in part 1). Also | − 2| 2, so 1 − 1 2 = | − 2| |2| 1 2 · 2 = . This shows that lim →2 (1) = 1 2. 37. 1. Guessing a value for Given 0, we must find 0 such that |√ − √| whenever 0 | − | . But |√ − √| = √| − + √| (from the hint). Now if we can find a positive constant such that √ + √ then °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.4 THE PRECISE DEFINITION OF A LIMIT ¤ 97 | − | √ + √ | − | , and we take | − | . We can find this number by restricting to lie in some interval centered at . If | − | 1 2, then − 1 2 − 1 2 ⇒ 1 2 3 2 ⇒ √ + √ 1 2 + √, and so = 1 2 + √ is a suitable choice for the constant. So | − | 1 2 + √. This suggests that we let = min 1 2 1 2 + √. 2. Showing that works Given 0, we let = min 1 2 1 2 + √. If 0 | − | , then | − | 1 2 ⇒ √ + √ 1 2 + √ (as in part 1). Also | − | 1 2 + √, so |√ − √ | = √| −+ √| 2 + 2 +√√ = . Therefore, lim → √ = √ by the definition of a limit. 38. Suppose that lim →0 () = . Given = 1 2, there exists 0 such that 0 || ⇒ |() − | 1 2 ⇔ − 1 2 () + 1 2. For 0 , () = 1, so 1 + 1 2 ⇒ 1 2. For − 0, () = 0, so − 1 2 0 ⇒ 1 2. This contradicts 1 2. Therefore, lim →0 () does not exist. 39. Suppose that lim →0 () = . Given = 1 2, there exists 0 such that 0 || ⇒ |() − | 1 2. Take any rational number with 0 || . Then () = 0, so |0 − | 1 2, so ≤ || 1 2. Now take any irrational number with 0 || . Then () = 1, so |1 − | 1 2. Hence, 1 − 1 2, so 1 2. This contradicts 1 2, so lim →0 () does not exist. 40. First suppose that lim → () = . Then, given 0 there exists 0 so that 0 | − | ⇒ |() − | . Then − ⇒ 0 | − | so |() − | . Thus, lim →− () = . Also + ⇒ 0 | − | so |() − | . Hence, lim →+ () = . Now suppose lim →− () = = lim →+ (). Let 0 be given. Since lim →− () = , there exists 1 0 so that − 1 ⇒ |() − | . Since lim →+ () = , there exists 2 0 so that + 2 ⇒ |() − | . Let be the smaller of 1 and 2. Then 0 | − | ⇒ − 1 or + 2 so |() − | . Hence, lim → () = . So we have proved that lim → () = ⇔ lim →− () = = lim →+ (). 41. 1 ( + 3)4 10,000 ⇔ ( + 3)4 10,1000 ⇔ | + 3| √4 101,000 ⇔ | − (−3)| 10 1 42. Given 0, we need 0 such that 0 | + 3| ⇒ 1( + 3)4 . Now 1 ( + 3)4 ⇔ ( + 3)4 1 ⇔ | + 3| √41 . So take = √41 . Then 0 | + 3| = √41 ⇒ ( + 3) 1 4 , so lim →−3 1 ( + 3)4 = ∞. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.98 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 43. Given 0 we need 0 so that ln whenever 0 ; that is, = ln whenever 0 . This suggests that we take = . If 0 , then ln ln = . By the definition of a limit, lim →0+ ln = −∞. 44. (a) Let be given. Since lim → () = ∞, there exists 1 0 such that 0 | − | 1 ⇒ () + 1 − . Since lim → () = , there exists 2 0 such that 0 | − | 2 ⇒ |() − | 1 ⇒ () − 1. Let be the smaller of 1 and 2. Then 0 | − | ⇒ () + () ( + 1 − ) + ( − 1) = . Thus, lim → [() + ()] = ∞. (b) Let 0 be given. Since lim → () = 0, there exists 1 0 such that 0 | − | 1 ⇒ |() − | 2 ⇒ () 2. Since lim → () = ∞, there exists 2 0 such that 0 | − | 2 ⇒ () 2. Let = min {1 2}. Then 0 | − | ⇒ () () 2 2 = , so lim → ()() = ∞. (c) Let 0 be given. Since lim → () = 0, there exists 1 0 such that 0 | − | 1 ⇒ |() − | −2 ⇒ () 2. Since lim → () = ∞, there exists 2 0 such that 0 | − | 2 ⇒ () 2. (Note that 0 and 0 ⇒ 2 0.) Let = min {1 2}. Then 0 | − | ⇒ () 2 ⇒ ()() 2 · 2 = , so lim → () () = −∞. 2.5 Continuity 1. From Definition 1, lim →4 () = (4). 2. The graph of has no hole, jump, or vertical asymptote. 3. (a) is discontinuous at −4 since (−4) is not defined and at −2, 2, and 4 since the limit does not exist (the left and right limits are not the same). (b) is continuous from the left at −2 since lim →−2− () = (−2). is continuous from the right at 2 and 4 since lim →2+ () = (2) and lim →4+ () = (4). It is continuous from neither side at −4 since (−4) is undefined. 4. From the graph of , we see that is continuous on the intervals [−3−2), (−2−1), (−1 0], (0 1), and (1 3]. 5. The graph of = () must have a discontinuity at = 2 and must show that lim →2+ () = (2). 6. The graph of = () must have discontinuities at = −1 and = 4. It must show that lim →−1− () = (−1) and lim →4+ () = (4). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.5 CONTINUITY ¤ 99 7. The graph of = () must have a removable discontinuity (a hole) at = 3 and a jump discontinuity at = 5. 8. The graph of = () must have a discontinuity at = −2 with lim →−2− () 6= (−2) and lim →−2+ () 6= (−2). It must also show that lim →2− () = (2) and lim →2+ () 6= (2). 9. (a) The toll is $7 between 7:00 AM and 10:00 AM and between 4:00 PM and 7:00 PM. (b) The function has jump discontinuities at = 7, 10, 16, and 19. Their significance to someone who uses the road is that, because of the sudden jumps in the toll, they may want to avoid the higher rates between = 7 and = 10 and between = 16 and = 19 if feasible. 10. (a) Continuous; at the location in question, the temperature changes smoothly as time passes, without any instantaneous jumps from one temperature to another. (b) Continuous; the temperature at a specific time changes smoothly as the distance due west from New York City increases, without any instantaneous jumps. (c) Discontinuous; as the distance due west from New York City increases, the altitude above sea level may jump from one height to another without going through all of the intermediate values— at a cliff, for example. (d) Discontinuous; as the distance traveled increases, the cost of the ride jumps in small increments. (e) Discontinuous; when the lights are switched on (or off ), the current suddenly changes between 0 and some nonzero value, without passing through all of the intermediate values. This is debatable, though, depending on your definition of current. 11. lim →−1 () = lim →−1 + 234 = lim →−1 + 2 lim →−1 34 = −1 + 2(−1)34 = (−3)4 = 81 = (−1). By the definition of continuity, is continuous at = −1. 12. lim →2 () = lim →2 2 + 5 2 + 1 = lim →2 (2 + 5) lim →2 (2 + 1) = lim →2 2 + 5 lim →2 2 lim →2 + lim →2 1 = 22 + 5(2) 2(2) + 1 = 14 5 = (2). By the definition of continuity, is continuous at = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.100 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 13. lim →1 () = lim →1 2√32 + 1 = 2 lim →1 √32 + 1 = 2lim →1(32 + 1) = 23 lim →1 2 + lim →1 1 = 23(1)2 + 1 = 2√4 = 4 = (1) By the definition of continuity, is continuous at = 1. 14. lim →2 () = lim →2 34 − 5 + √3 2 + 4 = 3 lim →2 4 − 5 lim →2 + 3 lim →2(2 + 4) = 3(2)4 − 5(2) + √3 22 + 4 = 48 − 10 + 2 = 40 = (2) By the definition of continuity, is continuous at = 2. 15. For 4, we have lim → () = lim → ( + √ − 4 ) = lim → + lim → √ − 4 [Limit Law 1] = + lim → − lim → 4 [8, 11, and 2] = + √ − 4 [8 and 7] = () So is continuous at = for every in (4 ∞). Also, lim →4+ () = 4 = (4), so is continuous from the right at 4. Thus, is continuous on [4 ∞). 16. For −2, we have lim → () = lim → − 1 3 + 6 = lim → ( − 1) lim → (3 + 6) [Limit Law 5] = lim → − lim → 1 3 lim → + lim → 6 [2 1 and 3] = − 1 3 + 6 [8 and 7] Thus, is continuous at = for every in (−∞ −2); that is, is continuous on (−∞ −2). 17. () = 1 + 2 is discontinuous at = −2 because (−2) is undefined. 18. () = 1 + 2 if 6= −2 1 if = −2 Here (−2) = 1, but lim →−2− () = −∞ and lim →−2+ () = ∞, so lim →−2 () does not exist and is discontinuous at −2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.5 CONTINUITY ¤ 101 19. () = 2+ 3 if if ≤ −−11 lim →−1− () = lim →−1− ( + 3) = −1 + 3 = 2 and lim →−1+ () = lim →−1+ 2 = 2−1 = 1 2. Since the left-hand and the right-hand limits of at −1 are not equal, lim →−1 () does not exist, and is discontinuous at −1. 20. () = 2 − 2 − 1 if 6= 1 1 if = 1 lim →1 () = lim →1 2 − 2 − 1 = lim →1 ( + 1)( ( −1) − 1) = lim →1 + 1 = 12, but (1) = 1, so is discontinous at 1 21. () = cos if 0 0 if = 0 1 − 2 if 0 lim →0 () = 1, but (0) = 0 6= 1, so is discontinuous at 0. 22. () = 22 − 5 − 3 − 3 if 6= 3 6 if = 3 lim →3 () = lim →3 22 − 5 − 3 − 3 = lim →3 (2 + 1)( − 3) − 3 = lim →3 (2 + 1) = 7, but (3) = 6, so is discontinuous at 3. 23. () = 2 − − 2 − 2 = ( − 2)( + 1) − 2 = + 1 for 6= 2. Since lim →2 () = 2 + 1 = 3, define (2) = 3. Then is continuous at 2. 24. () = 3 − 8 2 − 4 = ( − 2)(2 + 2 + 4) ( − 2)( + 2) = 2 + 2 + 4 + 2 for 6= 2. Since lim →2 () = 4 + 4 + 4 2 + 2 = 3, define (2) = 3. Then is continuous at 2. 25. () = 22 − − 1 2 + 1 is a rational function, so it is continuous on its domain, (−∞ ∞), by Theorem 5(b). 26. () = 2 + 1 22 − − 1 = 2 + 1 (2 + 1)( − 1) is a rational function, so it is continuous on its domain, −∞ − 1 2 ∪ − 1 2 1 ∪ (1 ∞), by Theorem 5(b). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.102 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 27. 3 − 2 = 0 ⇒ 3 = 2 ⇒ = √3 2, so () = √3 − 2 3 − 2 has domain −∞ √3 2 ∪ √3 2 ∞. Now 3 − 2 is continuous everywhere by Theorem 5(a) and √3 − 2 is continuous everywhere by Theorems 5(a), 7, and 9. Thus, is continuous on its domain by part 5 of Theorem 4. 28. The domain of () = sin 2 + cos is (−∞ ∞) since the denominator is never 0 [cos ≥ −1 ⇒ 2 + cos ≥ 1]. By Theorems 7 and 9, sin and cos are continuous on R. By part 1 of Theorem 4, 2 + cos is continuous on R and by part 5 of Theorem 4, is continuous on R. 29. By Theorem 5(a), the polynomial 1 + 2 is continuous on R. By Theorem 7, the inverse trigonometric function arcsin is continuous on its domain, [−1 1]. By Theorem 9, () = arcsin(1 + 2) is continuous on its domain, which is { | −1 ≤ 1 + 2 ≤ 1} = { | −2 ≤ 2 ≤ 0} = { | −1 ≤ ≤ 0} = [−1 0]. 30. By Theorem 7, the trigonometric function tan is continuous on its domain, | 6= 2 + . By Theorems 5(a), 7, and 9, the composite function √4 − 2 is continuous on its domain [−2 2]. By part 5 of Theorem 4, () = √tan 4 −2 is continuous on its domain, (−2 −2) ∪ (−2 2) ∪ (2 2). 31. () = 1 + 1 = + 1 is defined when + 1 ≥ 0 ⇒ + 1 ≥ 0 and 0 or + 1 ≤ 0 and 0 ⇒ 0 or ≤ −1, so has domain (−∞ −1] ∪ (0 ∞). is the composite of a root function and a rational function, so it is continuous at every number in its domain by Theorems 7 and 9. 32. By Theorems 7 and 9, the composite function −2 is continuous on R. By part 1 of Theorem 4, 1 + −2 is continuous on R. By Theorem 7, the inverse trigonometric function tan−1 is continuous on its domain, R. By Theorem 9, the composite function () = tan−11 + −2 is continuous on its domain, R. 33. The function = 1 1 + 1 is discontinuous at = 0 because the left- and right-hand limits at = 0 are different. 34. The function = tan2 is discontinuous at = 2 + , where is any integer. The function = lntan2 is also discontinuous where tan2 is 0, that is, at = . So = lntan2 is discontinuous at = 2 , any integer. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.5 CONTINUITY ¤ 103 35. Because is continuous on R and √20 − 2 is continuous on its domain, −√20 ≤ ≤ √20, the product () = √20 − 2 is continuous on −√20 ≤ ≤ √20. The number 2 is in that domain, so is continuous at 2, and lim →2 () = (2) = 2√16 = 8. 36. Because is continuous on R, sin is continuous on R, and + sin is continuous on R, the composite function () = sin( + sin ) is continuous on R, so lim → () = () = sin( + sin ) = sin = 0. 37. The function () = ln51 + − 2 is continuous throughout its domain because it is the composite of a logarithm function and a rational function. For the domain of , we must have 5 − 2 1 + 0, so the numerator and denominator must have the same sign, that is, the domain is (−∞ −√5 ] ∪ (−1 √5 ]. The number 1 is in that domain, so is continuous at 1, and lim →1 () = (1) = ln 5 − 1 1 + 1 = ln 2. 38. The function () = 3√2−2−4 is continuous throughout its domain because it is the composite of an exponential function, a root function, and a polynomial. Its domain is | 2 − 2 − 4 ≥ 0 = | 2 − 2 + 1 ≥ 5 = | ( − 1)2 ≥ 5 = | − 1| ≥ √5 = (−∞ 1 − √5 ] ∪ [1 + √5 ∞) The number 4 is in that domain, so is continuous at 4, and lim →4 () = (4) = 3√16−8−4 = 32 = 9. 39. () = 1 ln− 2 if if ≤ 1 1 By Theorem 5, since () equals the polynomial 1 − 2 on (−∞ 1], is continuous on (−∞ 1]. By Theorem 7, since () equals the logarithm function ln on (1 ∞), is continuous on (1 ∞). At = 1, lim →1− () = lim →1− (1 − 2) = 1 − 12 = 0 and lim →1+ () = lim →1+ ln = ln 1 = 0. Thus, lim →1 () exists and equals 0. Also, (1) = 1 − 12 = 0. Thus, is continuous at = 1. We conclude that is continuous on (−∞ ∞). 40. () = sin cos if if ≥ 44 By Theorem 7, the trigonometric functions are continuous. Since () = sin on (−∞ 4) and () = cos on (4 ∞), is continuous on (−∞ 4) ∪ (4 ∞) lim →(4)− () = lim →(4)− sin = sin 4 = 1√2 since the sine function is continuous at 4 Similarly, lim →(4)+ () = lim →(4)+ cos = 1√2 by continuity of the cosine function at 4. Thus, lim →(4) () exists and equals 1√2, which agrees with the value (4). Therefore, is continuous at 4, so is continuous on (−∞ ∞). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.104 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 41. () = 2 if −1 if − 1 ≤ 1 1 if ≥ 1 is continuous on (−∞ −1), (−1 1), and (1 ∞), where it is a polynomial, a polynomial, and a rational function, respectively. Now lim →−1− () = lim →−1− 2 = 1 and lim →−1+ () = lim →−1+ = −1, so is discontinuous at −1. Since (−1) = −1, is continuous from the right at −1. Also, lim →1− () = lim →1− = 1 and lim →1+ () = lim →1+ 1 = 1 = (1), so is continuous at 1. 42. () = 2 if ≤ 1 3 − if 1 ≤ 4 √ if 4 is continuous on (−∞ 1), (1 4), and (4 ∞), where it is an exponential, a polynomial, and a root function, respectively. Now lim →1− () = lim →1− 2 = 2 and lim →1+ () = lim →1+ (3 − ) = 2. Since (1) = 2 we have continuity at 1. Also, lim →4− () = lim →4− (3 − ) = −1 = (4) and lim →4+ () = lim →4+ √ = 2, so is discontinuous at 4, but it is continuous from the left at 4. 43. () = + 2 if 0 if 0 ≤ ≤ 1 2 − if 1 is continuous on (−∞ 0) and (1 ∞) since on each of these intervals it is a polynomial; it is continuous on (0 1) since it is an exponential. Now lim →0− () = lim →0− ( + 2) = 2 and lim →0+ () = lim →0+ = 1, so is discontinuous at 0. Since (0) = 1, is continuous from the right at 0. Also lim →1− () = lim →1− = and lim →1+ () = lim →1+ (2 − ) = 1, so is discontinuous at 1. Since (1) = , is continuous from the left at 1. 44. By Theorem 5, each piece of is continuous on its domain. We need to check for continuity at = . lim →− () = lim →− 3 = 2 and →lim+ () = lim →+ 2 = 2 , so lim → () = 2 . Since () = 2 , is continuous at . Therefore, is a continuous function of . 45. () = 32−+ 2 if if ≥ 2 2 is continuous on (−∞ 2) and (2 ∞). Now lim →2− () = lim →2− 2 + 2 = 4 + 4 and °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.5 CONTINUITY ¤ 105 lim →2+ () = lim →2+ 3 − = 8 − 2. So is continuous ⇔ 4 + 4 = 8 − 2 ⇔ 6 = 4 ⇔ = 2 3. Thus, for to be continuous on (−∞ ∞), = 2 3. 46. () = 2 − 4 − 2 if 2 2 − + 3 if 2 ≤ 3 2 − + if ≥ 3 At = 2: lim →2− () = lim →2− 2 − 4 − 2 = lim →2− ( + 2)( − 2) − 2 = lim →2− ( + 2) = 2 + 2 = 4 lim →2+ () = lim →2+ (2 − + 3) = 4 − 2 + 3 We must have 4 − 2 + 3 = 4, or 4 − 2 = 1 (1). At = 3: lim →3− () = lim →3− (2 − + 3) = 9 − 3 + 3 lim →3+ () = lim →3+ (2 − + ) = 6 − + We must have 9 − 3 + 3 = 6 − + , or 10 − 4 = 3 (2). Now solve the system of equations by adding −2 times equation (1) to equation (2). −8 + 4 = −2 10 − 4 = 3 2 = 1 So = 1 2. Substituting 1 2 for in (1) gives us −2 = −1, so = 1 2 as well. Thus, for to be continuous on (−∞ ∞), = = 1 2. 47. If and are continuous and (2) = 6, then lim →2 [3() + () ()] = 36 ⇒ 3 lim →2 () + lim →2 () · lim →2 () = 36 ⇒ 3(2) + (2) · 6 = 36 ⇒ 9(2) = 36 ⇒ (2) = 4. 48. (a) () = 1 and () = 1 2 , so ( ◦ )() = (()) = (12) = 1 (12) = 2. (b) The domain of ◦ is the set of numbers in the domain of (all nonzero reals) such that () is in the domain of (also all nonzero reals). Thus, the domain is 6= 0 and 12 6= 0 = { | 6= 0} or (−∞ 0) ∪ (0 ∞). Since ◦ is the composite of two rational functions, it is continuous throughout its domain; that is, everywhere except = 0. 49. (a) () = 4 − 1 − 1 = (2 + 1)(2 − 1) − 1 = (2 + 1)( + 1)( − 1) − 1 = (2 + 1)( + 1) [or 3 + 2 + + 1] for 6= 1. The discontinuity is removable and () = 3 + 2 + + 1 agrees with for 6= 1 and is continuous on R. (b) () = 3 − 2 − 2 − 2 = (2 − − 2) − 2 = ( − 2)( + 1) − 2 = ( + 1) [or 2 + ] for 6= 2. The discontinuity is removable and () = 2 + agrees with for 6= 2 and is continuous on R. (c) lim →− () = lim →− [[sin ]] = lim →− 0 = 0 and lim →+ () = lim →+ [[sin ]] = lim →+ (−1) = −1, so lim → () does not exist. The discontinuity at = is a jump discontinuity. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.106 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 50. does not satisfy the conclusion of the Intermediate Value Theorem. does satisfy the conclusion of the Intermediate Value Theorem. 51. () = 2 + 10 sin is continuous on the interval [31 32], (31) ≈ 957, and (32) ≈ 1030. Since 957 1000 1030, there is a number c in (31 32) such that () = 1000 by the Intermediate Value Theorem. Note: There is also a number c in (−32 −31) such that () = 1000 52. Suppose that (3) 6. By the Intermediate Value Theorem applied to the continuous function on the closed interval [2 3], the fact that (2) = 8 6 and (3) 6 implies that there is a number in (2 3) such that () = 6. This contradicts the fact that the only solutions of the equation () = 6 are = 1 and = 4. Hence, our supposition that (3) 6 was incorrect. It follows that (3) ≥ 6. But (3) 6= 6 because the only solutions of () = 6 are = 1 and = 4. Therefore, (3) 6. 53. () = 4 + − 3 is continuous on the interval [1 2] (1) = −1, and (2) = 15. Since −1 0 15, there is a number in (1 2) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation 4 + − 3 = 0 in the interval (1 2) 54. The equation ln = − √ is equivalent to the equation ln − + √ = 0. () = ln − + √ is continuous on the interval [2 3], (2) = ln 2 − 2 + √2 ≈ 0107, and (3) = ln 3 − 3 + √3 ≈ −0169. Since (2) 0 (3), there is a number in (2 3) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation ln − + √ = 0, or ln = − √, in the interval (2 3). 55. The equation = 3 − 2 is equivalent to the equation + 2 − 3 = 0. () = + 2 − 3 is continuous on the interval [0 1], (0) = −2, and (1) = − 1 ≈ 172. Since −2 0 − 1, there is a number in (0 1) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation + 2 − 3 = 0, or = 3 − 2, in the interval (0 1). 56. The equation sin = 2 − is equivalent to the equation sin − 2 + = 0. () = sin − 2 + is continuous on the interval [1 2] (1) = sin 1 ≈ 084, and (2) = sin 2 − 2 ≈ −109. Since sin 1 0 sin 2 − 2, there is a number in (1 2) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation sin − 2 + = 0, or sin = 2 − , in the interval (1 2). 57. (a) () = cos − 3 is continuous on the interval [0 1], (0) = 1 0, and (1) = cos 1 − 1 ≈ −046 0. Since 1 0 −046, there is a number in (0 1) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation cos − 3 = 0, or cos = 3, in the interval (0 1). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.5 CONTINUITY ¤ 107 (b) (086) ≈ 0016 0 and (087) ≈ −0014 0, so there is a root between 086 and 087, that is, in the interval (086 087). 58. (a) () = ln − 3 + 2 is continuous on the interval [1 2], (1) = −1 0, and (2) = ln 2 + 1 ≈ 17 0. Since −1 0 17, there is a number in (1 2) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation ln − 3 + 2 = 0, or ln = 3 − 2, in the interval (1 2). (b) (134) ≈ −003 0 and (135) ≈ 00001 0, so there is a root between 134 and 135 that is, in the interval (134 135). 59. (a) Let () = 100−100 − 0012 Then (0) = 100 0 and (100) = 100−1 − 100 ≈ −632 0. So by the Intermediate Value Theorem, there is a number in (0 100) such that () = 0. This implies that 100−100 = 0012. (b) Using the intersect feature of the graphing device, we find that the root of the equation is = 70347, correct to three decimal places. 60. (a) Let () = arctan + − 1. Then (0) = −1 0 and (1) = 4 0. So by the Intermediate Value Theorem, there is a number in (0 1) such that () = 0. This implies that arctan = 1 − . (b) Using the intersect feature of the graphing device, we find that the root of the equation is = 0520, correct to three decimal places. 61. Let () = sin 3. Then is continuous on [1 2] since is the composite of the sine function and the cubing function, both of which are continuous on R. The zeros of the sine are at , so we note that 0 1 3 2 2 8 3, and that the pertinent cube roots are related by 1 3 3 2 [call this value ] 2. [By observation, we might notice that = √3 and = √3 2 are zeros of .] Now (1) = sin 1 0, () = sin 3 2 = −1 0, and (2) = sin 8 0. Applying the Intermediate Value Theorem on [1 ] and then on [ 2], we see there are numbers and in (1 ) and ( 2) such that () = () = 0. Thus, has at least two -intercepts in (1 2). 62. Let () = 2 − 3 + 1. Then is continuous on (0 2] since is a rational function whose domain is (0 ∞). By inspection, we see that 1 4 = 17 16 0, (1) = −1 0, and (2) = 3 2 0. Appling the Intermediate Value Theorem on 1 4 1 and then on [1 2], we see there are numbers and in 1 4 1 and (1 2) such that () = () = 0. Thus, has at least two -intercepts in (0 2). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.108 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 63. (⇒) If is continuous at , then by Theorem 8 with () = + , we have lim →0 ( + ) = lim →0 ( + ) = (). (⇐) Let 0. Since lim →0 ( + ) = (), there exists 0 such that 0 || ⇒ |( + ) − ()| . So if 0 | − | , then |() − ()| = |( + ( − )) − ()| . Thus, lim → () = () and so is continuous at . 64. lim →0 sin( + ) = lim →0 (sin cos + cos sin ) = lim →0 (sin cos ) + lim →0 (cos sin ) = lim →0 sin lim →0 cos + lim →0 cos lim →0 sin = (sin )(1) + (cos )(0) = sin 65. As in the previous exercise, we must show that lim →0 cos( + ) = cos to prove that the cosine function is continuous. lim →0 cos( + ) = lim →0 (cos cos − sin sin ) = lim →0 (cos cos ) − lim →0 (sin sin ) = lim →0 cos lim →0 cos − lim →0 sin lim →0 sin = (cos )(1) − (sin )(0) = cos 66. (a) Since is continuous at , lim → () = (). Thus, using the Constant Multiple Law of Limits, we have lim → ( )() = lim → () = lim → () = () = ( )(). Therefore, is continuous at . (b) Since and are continuous at , lim → () = () and lim → () = (). Since () 6= 0, we can use the Quotient Law of Limits: lim → () = lim → (()) = lim lim → () → () = () () = (). Thus, is continuous at . 67. () = 0 1 if if is rational is irrational is continuous nowhere. For, given any number and any 0, the interval ( − + ) contains both infinitely many rational and infinitely many irrational numbers. Since () = 0 or 1, there are infinitely many numbers with 0 | − | and |() − ()| = 1. Thus, lim → () 6= (). [In fact, lim → () does not even exist.] 68. () = 0 if if is rational is irrational is continuous at 0. To see why, note that − || ≤ () ≤ ||, so by the Squeeze Theorem lim →0 () = 0 = (0). But is continuous nowhere else. For if 6= 0 and 0, the interval ( − + ) contains both infinitely many rational and infinitely many irrational numbers. Since () = 0 or , there are infinitely many numbers with 0 | − | and |() − ()| || 2. Thus, lim → () 6= (). 69. If there is such a number, it satisfies the equation 3 + 1 = ⇔ 3 − + 1 = 0. Let the left-hand side of this equation be called (). Now (−2) = −5 0, and (−1) = 1 0. Note also that () is a polynomial, and thus continuous. So by the Intermediate Value Theorem, there is a number between −2 and −1 such that () = 0, so that = 3 + 1. 70. 3 + 22 − 1 + 3 + − 2 = 0 ⇒ (3 + − 2) + (3 + 22 − 1) = 0. Let () denote the left side of the last equation. Since is continuous on [−1 1], (−1) = −4 0, and (1) = 2 0, there exists a in (−1 1) such that °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 109 () = 0 by the Intermediate Value Theorem. Note that the only root of either denominator that is in (−1 1) is (−1 + √5 )2 = , but () = (3 √5 − 9)2 6= 0. Thus, is not a root of either denominator, so () = 0 ⇒ = is a root of the given equation. 71. () = 4 sin(1) is continuous on (−∞ 0) ∪ (0 ∞) since it is the product of a polynomial and a composite of a trigonometric function and a rational function. Now since −1 ≤ sin(1) ≤ 1, we have −4 ≤ 4 sin(1) ≤ 4. Because lim →0 (−4) = 0 and lim →0 4 = 0, the Squeeze Theorem gives us lim →0 (4 sin(1)) = 0, which equals (0). Thus, is continuous at 0 and, hence, on (−∞ ∞). 72. (a) lim →0+ () = 0 and lim →0− () = 0, so lim →0 () = 0, which is (0), and hence is continuous at = if = 0. For 0, lim → () = lim → = = (). For 0, lim → () = lim → (−) = − = (). Thus, is continuous at = ; that is, continuous everywhere. (b) Assume that is continuous on the interval . Then for ∈ , lim → |()| = lim → () = |()| by Theorem 8. (If is an endpoint of , use the appropriate one-sided limit.) So || is continuous on . (c) No, the converse is false. For example, the function () = −11 if if ≥ 00 is not continuous at = 0, but |()| = 1 is continuous on R. 73. Define () to be the monk’s distance from the monastery, as a function of time (in hours), on the first day, and define () to be his distance from the monastery, as a function of time, on the second day. Let be the distance from the monastery to the top of the mountain. From the given information we know that (0) = 0, (12) = , (0) = and (12) = 0. Now consider the function − , which is clearly continuous. We calculate that ( − )(0) = − and ( − )(12) = . So by the Intermediate Value Theorem, there must be some time 0 between 0 and 12 such that ( − )(0) = 0 ⇔ (0) = (0). So at time 0 after 7:00 AM, the monk will be at the same place on both days. 2.6 Limits at Infinity; Horizontal Asymptotes 1. (a) As becomes large, the values of () approach 5. (b) As becomes large negative, the values of () approach 3. 2. (a) The graph of a function can intersect a vertical asymptote in the sense that it can meet but not cross it. The graph of a function can intersect a horizontal asymptote. It can even intersect its horizontal asymptote an infinite number of times. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.110 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (b) The graph of a function can have 0, 1, or 2 horizontal asymptotes. Representative examples are shown. No horizontal asymptote One horizontal asymptote Two horizontal asymptotes 3. (a) lim →∞ () = −2 (b) lim →−∞ () = 2 (c) lim →1 () = ∞ (d) lim →3 () = −∞ (e) Vertical: = 1, = 3; horizontal: = −2, = 2 4. (a) lim →∞ () = 2 (b) lim →−∞ () = −1 (c) lim →0 () = −∞ (d) lim →2− () = −∞ (e) lim →2+ () = ∞ (f ) Vertical: = 0, = 2; horizontal: = −1, = 2 5. lim →0 () = −∞, lim →−∞ () = 5, lim →∞ () = −5 6. lim →2 () = ∞, lim →−2+ () = ∞, lim →−2− () = −∞, lim →−∞ () = 0, lim →∞ () = 0, (0) = 0 7. lim →2 () = −∞, lim →∞ () = ∞, lim →−∞ () = 0, lim →0+ () = ∞, lim →0− () = −∞ 8. lim →∞ () = 3, lim →2− () = ∞, lim →2+ () = −∞, is odd 9. (0) = 3, lim →0− () = 4, lim →0+ () = 2, lim →−∞ () = −∞, lim →4− () = −∞, lim →4+ () = ∞, lim →∞ () = 3 10. lim →3 () = −∞, lim →∞ () = 2, (0) = 0, is even °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 111 11. If () = 22, then a calculator gives (0) = 0, (1) = 05, (2) = 1, (3) = 1125, (4) = 1, (5) = 078125, (6) = 05625, (7) = 03828125, (8) = 025, (9) = 0158203125, (10) = 009765625, (20) ≈ 000038147, (50) ≈ 22204 × 10−12, (100) ≈ 78886 × 10−27. It appears that lim →∞ 22 = 0. 12. (a) From a graph of () = (1 − 2) in a window of [0 10,000] by [0 02], we estimate that lim →∞ () = 014 (to two decimal places.) (b) () 10,000 0135 308 100,000 0135 333 1,000,000 0135 335 From the table, we estimate that lim →∞ () = 01353 (to four decimal places.) 13. lim →∞ 22 − 7 52 + − 3 = lim →∞ (5(22+2 − −7) 3) 2 2 [Divide both the numerator and denominator by (the highest power of that appears in the denominator)] 2 = lim →∞ (2 − 72) lim →∞ (5 + 1 − 32) [Limit Law 5] = lim →∞ 2 − lim →∞ (72) lim →∞ 5 + lim →∞ (1) − lim →∞ (32) [Limit Laws 1 and 2] = 2 − 7 lim →∞ (12) 5 + lim →∞ (1) − 3 lim →∞ (12) [Limit Laws 7 and 3] = 2 − 7(0) 5 + 0 + 3(0) [Theorem 2.6.5] = 2 5 14. lim →∞ 93−3 + 8 5 +−34 = lim →∞ 93−3 + 8 5 +−34 [Limit Law 11] = lim →∞ 9 + 8 33 − 52 −24 + 13 [Divide by 3] = lim →∞ (9 + 82 − 43) lim →∞ (33 − 52 + 1) [Limit Law 5] = lim →∞ 9 + lim →∞ (82) − lim →∞ (43) lim →∞ (33) − lim →∞ (52) + lim →∞ 1 [Limit Laws 1 and 2] = 9 + 8 lim →∞ (12) − 4 lim →∞ (13) 3 lim →∞ (13) − 5 lim →∞ (12) + 1 [Limit Laws 7 and 3] = 9 + 8(0) 3(0) − 5(0) + 1 − 4(0) [Theorem 2.6.5] = 9 1 = √9 = 3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.112 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 15. lim →∞ 3 − 2 2 + 1 = lim →∞ (3 − 2) (2 + 1) = lim →∞ 3 2 + 1 − 2 = lim →∞ lim 3 − 2 lim →∞1 →∞ 2 + lim →∞ 1 = 3 − 2(0) 2 + 0 = 3 2 16. lim →∞ 1 − 2 3 − + 1 = lim →∞ ((1 3 −−+ 1) 2) 3 3 = lim →∞ 1 −1 1 3 2−+ 1 13 = lim →∞ 13 − lim →∞ 1 lim →∞ 1 − lim →∞ 12 + lim →∞ 13 = 0 − 0 1 − 0 + 0 = 0 17. lim →−∞ − 2 2 + 1 = lim →−∞ ((2−+ 1) 2) 22 = lim →−∞ 1 1 + 1 − 22 2 = →−∞ limlim1 − 2 lim →−∞12 →−∞ 1 + lim →−∞ 12 = 0 − 2(0) 1 + 0 = 0 18. lim →−∞ 43 + 62 − 2 23 − 4 + 5 = lim →−∞ (4 (233+ 6 − 42+ 5) − 2) 33 = lim →−∞ 24 + 6 − 4 2−+ 5 2 33 = 4 + 0 2 − 0 + 0 − 0 = 2 19. lim →∞ √ + 2 2 − 2 = lim →∞ ((2 √−+22)) 22 = lim →∞ 1 2 32−+ 1 1 = 0 + 1 0 − 1 = −1 20. lim →∞ − √ 232 + 3 − 5 = lim →∞ − √ 32 (232 + 3 − 5) 32 = lim →∞ 2 + 31 1122−−5132 = 2 + 0 0 −−1 0 = −12 21. lim →∞ (22 + 1)2 ( − 1)2(2 + ) = lim →∞ [( −(21) 22+ 1) (2 +2 )] 44 = lim →∞ [(2 − 2[(2+ 1) 2 + 1) 2][( 22]2+ )2] = lim →∞ (2 + 12)2 (1 − 2 + 12)(1 + 1) = (2 + 0)2 (1 − 0 + 0)(1 + 0) = 4 22. lim →∞ 2 √4 + 1 = lim →∞ √42+ 1 22 = lim →∞ (4 + 1) 1 4 [since 2 = √4 for 0] = lim →∞ 1 1 + 14 = 1 √1 + 0 = 1 23. lim →∞ √1 + 46 2 − 3 = lim →∞ √1 + 463 (2 − 3)3 = lim →∞ (1 + 46)6 lim →∞ (23 − 1) [since 3 = √6 for 0] = lim →∞ 16 + 4 lim →∞ (23) − lim →∞ 1 = lim →∞(16) + lim →∞4 0 − 1 = √0 + 4 −1 = 2 − 1 = −2 24. lim →−∞ √1 + 46 2 − 3 = lim →−∞ √1 + 463 (2 − 3)3 = lim →−∞ −(1 + 46)6 lim →−∞ (23 − 1) [since 3 = −√6 for 0] = lim →−∞ −16 + 4 2 lim →−∞ (13) − lim →−∞ 1 = −→−∞ lim (16) + lim →−∞4 2(0) − 1 = −√0 + 4 −1 = −2 −1 = 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 113 25. lim →∞ √ + 32 4 − 1 = lim →∞ √ + 32 (4 − 1) = lim →∞ ( + 32)2 lim →∞ (4 − 1) [since = √2 for 0] = lim →∞ 1 + 3 lim →∞ 4 − lim →∞ (1) = lim →∞(1) + lim →∞3 4 − 0 = √0 + 3 4 = √3 4 26. lim →∞ + 32 4 − 1 = lim →∞ ((4 + 3 −1) 2) = lim →∞ 41 + 3 − 1 = ∞ since 1 + 3 → ∞ and 4 − 1 → 4 as → ∞. 27. lim →∞ √92 + − 3 = lim →∞ √92 + − 3√92 + + 3 √92 + + 3 = lim →∞ √92 + 2 − (3)2 √92 + + 3 = lim →∞ 92 + − 92 √92 + + 3 = lim →∞ √92 + + 3 · 11 = lim →∞ 922 + 2 + 3 = lim →∞ 9 + 11 + 3 = √9 + 3 1 = 3 + 3 1 = 1 6 28. lim →−∞ √42 + 3 + 2 = lim →−∞ √42 + 3 + 2 √√4 4 2 2 + 3 + 3 − − 2 2 = lim →−∞ 42 + 3 − (2)2 √42 + 3 − 2 = lim →−∞ √42 + 3 3 − 2 = lim →−∞ 3 √42 + 3 − 2 = lim →−∞ −4 + 3 3 − 2 [since = −√2 for 0] = 3 −√4 + 0 − 2 = − 3 4 29. lim →∞ √2 + − √2 + = lim →∞ √2 + − √2 + √2 + + √2 + √2 + + √2 + = lim →∞ (2 + ) − (2 + ) √2 + + √2 + = lim →∞ √2 + [(+−√)2]+ √2 = lim →∞ − 1 + + 1 + = − √1 + 0 + √1 + 0 = − 2 30. For 0, √2 + 1 √2 = . So as → ∞, we have √2 + 1 → ∞, that is, lim →∞ √2 + 1 = ∞. 31. lim →∞ 4 − 32 + 3 − + 2 = lim →∞ ((4 3−−32+ 2) + )3 3 divide by the highest power of in the denominator = lim →∞ 1−−13 2+ 1 + 2 23 = ∞ since the numerator increases without bound and the denominator approaches 1 as → ∞. 32. lim →∞ (− + 2 cos 3) does not exist. lim →∞ − = 0, but lim →∞ (2 cos 3) does not exist because the values of 2 cos 3 oscillate between the values of −2 and 2 infinitely often, so the given limit does not exist. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.114 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 33. lim →−∞ (2 + 27) = lim →−∞ 7 15 + 2 [factor out the largest power of ] = −∞ because 7 → −∞ and 15 + 2 → 2 as → −∞. Or: lim →−∞ 2 + 27 = lim →−∞ 2 1 + 25 = −∞. 34. lim →−∞ 1 + 6 4 + 1 = lim →−∞ (1 + (4 + 1) 6) 4 4 divide by the highest power of in the denominator = lim →−∞ 11 + 1 4 +42 = ∞ since the numerator increases without bound and the denominator approaches 1 as → −∞. 35. Let = . As → ∞, → ∞. lim →∞ arctan() = lim →∞ arctan = 2 by (3). 36. Divide numerator and denominator by 3: lim →∞ 3 − −3 3 + −3 = lim →∞ 1 1 +− − −6 6 = 11 + 0 − 0 = 1 37. lim →∞ 1 − 1 + 2 = lim →∞ (1 − ) (1 + 2) = lim →∞ 1 1 − + 2 1 = 00 + 2 − 1 = −1 2 38. Since 0 ≤ sin2 ≤ 1, we have 0 ≤ sin2 2 + 1 ≤ 2 1+ 1. We know that lim →∞0 = 0 and lim →∞ 2 1+ 1 = 0, so by the Squeeze Theorem, lim →∞ sin2 2 + 1 = 0. 39. Since −1 ≤ cos ≤ 1 and −2 0, we have −−2 ≤ −2 cos ≤ −2. We know that lim →∞ (−−2) = 0 and lim →∞ −2 = 0, so by the Squeeze Theorem, lim →∞ (−2 cos ) = 0. 40. Let = ln . As → 0+, → −∞. lim →0+ tan−1(ln ) = lim →−∞ tan−1 = − 2 by (4). 41. lim →∞ [ln(1 + 2) − ln(1 + )] = lim →∞ ln 1 + 2 1 + = ln lim →∞ 1 + 1 +2 = ln lim →∞ 1 1 ++ 1 = ∞, since the limit in parentheses is ∞. 42. lim →∞ [ln(2 + ) − ln(1 + )] = lim →∞ ln 1 + 2 + = lim →∞ln 21 + 1 + 1 = ln 11 = ln 1 = 0 43. (a) (i) lim →0+ () = lim →0+ ln = 0 since → 0+ and ln → −∞ as → 0+. (ii) lim →1− () = lim →1− ln = −∞ since → 1 and ln → 0− as → 1−. (iii) lim →1+ () = lim →1+ ln = ∞ since → 1 and ln → 0+ as → 1+. (b) () 10,000 10857 100,000 86859 1,000,000 72,3824 It appears that lim →∞ () = ∞. (c) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 115 44. (a) lim →∞ () = lim →∞2 − ln1 = 0 since 2 → 0 and 1 ln → 0 as → ∞. (e) (b) lim →0+ () = lim →0+ 2 − ln1 = ∞ since 2 → ∞ and 1 ln → 0 as → 0+. (c) lim →1− () = lim →1− 2 − ln1 = ∞ since 2 → 2 and ln1 → −∞ as → 1−. (d) lim →1+ () = lim →1+ 2 − ln1 = −∞ since 2 → 2 and ln1 → ∞ as → 1+. 45. (a) From the graph of () = √2 + + 1 + , we estimate the value of lim →−∞ () to be −05. (b) () −10,000 −0499 962 5 −100,000 −0499 996 2 −1,000,000 −0499 999 6 From the table, we estimate the limit to be −05. (c) lim →−∞ √2 + + 1 + = lim →−∞ √2 + + 1 + √√ 2 2 + + + 1 + 1 − − = lim →−∞ √22+++ 1 + 1 −−2 = lim →−∞ ( + 1)(1) √2 + + 1 − (1) = lim →−∞ −1 + (1 1 + (1 ) + (1 )2) − 1 = 1 + 0 −√1 + 0 + 0 − 1 = − 1 2 Note that for 0, we have √2 = || = −, so when we divide the radical by , with 0, we get 1 √2 + + 1 = −√12 √2 + + 1 = −1 + (1) + (12). 46. (a) From the graph of () = √32 + 8 + 6 − √32 + 3 + 1, we estimate (to one decimal place) the value of lim →∞ () to be 14. (b) () 10,000 1443 39 100,000 1443 38 1,000,000 1443 38 From the table, we estimate (to four decimal places) the limit to be 14434. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.116 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (c) lim →∞ () = lim →∞ √32 + 8 + 6 − √32 + 3 + 1 √32 + 8 + 6 + √32 + 3 + 1 √32 + 8 + 6 + √32 + 3 + 1 = lim →∞ 32 + 8 + 6 − 32 + 3 + 1 √32 + 8 + 6 + √32 + 3 + 1 = lim →∞ √32 + 8 + 6 + (5 + 5)(1 √32 + 3 ) + 1 (1) = lim →∞ 5 + 5 3 + 8 + 62 + 3 + 3 + 12 = 5 √3 + √3 = 5 2 √3 = 5 √3 6 ≈ 1443376 47. lim →±∞ 5 + 4 + 3 = lim →±∞ (5 + 4) ( + 3) = lim →±∞ 5 1 + 3 + 4 = 0 + 4 1 + 0 = 4, so = 4 is a horizontal asymptote. = () = 5 + 4 + 3 , so lim →−3+ () = −∞ since 5 + 4 → −7 and + 3 → 0+ as → −3+. Thus, = −3 is a vertical asymptote. The graph confirms our work. 48. lim →±∞ 22 + 1 32 + 2 − 1 = lim →±∞ (3(2 2 + 2 2 + 1) − 1)22 = lim →±∞ 2 + 12 3 + 2 − 12 = 2 3 so = 2 3 is a horizontal asymptote. = () = 22 + 1 32 + 2 − 1 = 22 + 1 (3 − 1)( + 1). The denominator is zero when = 1 3 and −1, but the numerator is nonzero, so = 1 3 and = −1 are vertical asymptotes. The graph confirms our work. 49. lim →±∞ 22 + − 1 2 + − 2 = lim →±∞ 22 + − 1 2 2 + − 2 2 = lim →±∞ 2 + 1 − 1 2 1 + 1 − 2 2 = lim →±∞2 + 1 − 12 lim →±∞1 + 1 − 22 = lim →±∞ 2 + lim →±∞ 1 − lim →±∞ 1 2 lim →±∞ 1 + lim →±∞ 1 − 2 lim →±∞ 1 2 = 2 + 0 − 0 1 + 0 − 2(0) = 2, so = 2 is a horizontal asymptote. = () = 22 + − 1 2 + − 2 = (2 − 1)( + 1) ( + 2)( − 1) , so →− lim2− () = ∞, lim →−2+ () = −∞, lim →1− () = −∞, and lim →1+ () = ∞. Thus, = −2 and = 1 are vertical asymptotes. The graph confirms our work. 50. lim →±∞ 1 + 4 2 − 4 = lim →±∞ 1 + 4 4 2 − 4 4 = lim →±∞ 1 4 + 1 1 2 − 1 = lim →±∞14 + 1 lim →±∞12 − 1 = lim →±∞ 1 4 + lim →±∞ 1 lim →±∞ 1 2 − lim →±∞ 1 = 0 + 1 0 − 1 = −1, so = −1 is a horizontal asymptote. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 117 = () = 1 + 4 2 − 4 = 1 + 4 2(1 − 2) = 1 + 4 2(1 + )(1 − ). The denominator is zero when = 0, −1, and 1, but the numerator is nonzero, so = 0, = −1, and = 1 are vertical asymptotes. Notice that as → 0, the numerator and denominator are both positive, so lim →0 () = ∞. The graph confirms our work. 51. = () = 3 − 2 − 6 + 5 = (2 − 1) ( − 1)( − 5) = ( + 1)( − 1) ( − 1)( − 5) = ( + 1) − 5 = () for 6= 1. The graph of is the same as the graph of with the exception of a hole in the graph of at = 1. By long division, () = 2 + − 5 = + 6 + 30 − 5 . As → ±∞, () → ±∞, so there is no horizontal asymptote. The denominator of is zero when = 5. lim →5− () = −∞ and lim →5+ () = ∞, so = 5 is a vertical asymptote. The graph confirms our work. 52. lim →∞ 2 − 5 = lim →∞ 2 − 5 · 1 1 = lim →∞ 1 − (5 2) = 1 −2 0 = 2, so = 2 is a horizontal asymptote. lim →−∞ 2 − 5 = 2(0) 0 − 5 = 0, so = 0 is a horizontal asymptote. The denominator is zero (and the numerator isn’t) when − 5 = 0 ⇒ = 5 ⇒ = ln 5. lim →(ln 5)+ 2 − 5 = ∞ since the numerator approaches 10 and the denominator approaches 0 through positive values as → (ln 5)+. Similarly, lim →(ln 5)− 2 − 5 = −∞. Thus, = ln 5 is a vertical asymptote. The graph confirms our work. 53. From the graph, it appears = 1 is a horizontal asymptote. lim →±∞ 33 + 5002 3 + 5002 + 100 + 2000 = lim →±∞ 33 + 5002 3 3 + 5002 + 100 + 2000 3 = lim →±∞ 3 + (500) 1 + (500) + (1002) + (20003) = 3 + 0 1 + 0 + 0 + 0 = 3, so = 3 is a horizontal asymptote. The discrepancy can be explained by the choice of the viewing window. Try [−100,000 100,000] by [−1 4] to get a graph that lends credibility to our calculation that = 3 is a horizontal asymptote. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.118 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 54. (a) From the graph, it appears at first that there is only one horizontal asymptote, at ≈ 0 and a vertical asymptote at ≈ 17. However, if we graph the function with a wider and shorter viewing rectangle, we see that in fact there seem to be two horizontal asymptotes: one at ≈ 05 and one at ≈ −05. So we estimate that lim →∞ √22 + 1 3 − 5 ≈ 05 and lim →−∞ √22 + 1 3 − 5 ≈ −05 (b) (1000) ≈ 04722 and (10,000) ≈ 04715, so we estimate that lim →∞ √22 + 1 3 − 5 ≈ 047. (−1000) ≈ −04706 and (−10,000) ≈ −04713, so we estimate that lim →−∞ √22 + 1 3 − 5 ≈ −047. (c) lim →∞ √22 + 1 3 − 5 = lim →∞ 2 + 12 3 − 5 [since √2 = for 0] = √2 3 ≈ 0471404. For 0, we have √2 = || = −, so when we divide the numerator by , with 0, we get 1 √22 + 1 = −√12 √22 + 1 = −2 + 12. Therefore, lim →−∞ √22 + 1 3 − 5 = lim →−∞ −2 + 12 3 − 5 = − √2 3 ≈ −0471404. 55. Divide the numerator and the denominator by the highest power of in (). (a) If deg deg , then the numerator → 0 but the denominator doesn’t. So lim →∞ [ ()()] = 0. (b) If deg deg , then the numerator → ±∞ but the denominator doesn’t, so lim →∞ [ ()()] = ±∞ (depending on the ratio of the leading coefficients of and ). 56. (i) = 0 (ii) 0 ( odd) (iii) 0 ( even) (iv) 0 ( odd) (v) 0 ( even) From these sketches we see that (a) lim →0+ = 1 if = 0 0 if 0 ∞ if 0 (b) lim →0− = 1 if = 0 0 if 0 −∞ if 0, odd ∞ if 0, even °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 119 (c) lim →∞ = 1 if = 0 ∞ if 0 0 if 0 (d) lim →−∞ = 1 if = 0 −∞ if 0, odd ∞ if 0, even 0 if 0 57. Let’s look for a rational function. (1) lim →±∞ () = 0 ⇒ degree of numerator degree of denominator (2) lim →0 () = −∞ ⇒ there is a factor of 2 in the denominator (not just , since that would produce a sign change at = 0), and the function is negative near = 0. (3) lim →3− () = ∞ and lim →3+ () = −∞ ⇒ vertical asymptote at = 3; there is a factor of ( − 3) in the denominator. (4) (2) = 0 ⇒ 2 is an -intercept; there is at least one factor of ( − 2) in the numerator. Combining all of this information and putting in a negative sign to give us the desired left- and right-hand limits gives us () = 2 − 2( − 3) as one possibility. 58. Since the function has vertical asymptotes = 1 and = 3, the denominator of the rational function we are looking for must have factors ( − 1) and ( − 3). Because the horizontal asymptote is = 1, the degree of the numerator must equal the degree of the denominator, and the ratio of the leading coefficients must be 1. One possibility is () = 2 ( − 1)( − 3). 59. (a) We must first find the function . Since has a vertical asymptote = 4 and -intercept = 1, − 4 is a factor of the denominator and − 1 is a factor of the numerator. There is a removable discontinuity at = −1, so − (−1) = + 1 is a factor of both the numerator and denominator. Thus, now looks like this: () = ( − 1)( + 1) ( − 4)( + 1) , where is still to be determined. Then lim →−1 () = lim →−1 ( − 1)( + 1) ( − 4)( + 1) = lim →−1 (−−41) = ((−−11−−4) 1) = 25, so 25 = 2, and = 5. Thus () = 5( − 1)( + 1) ( − 4)( + 1) is a ratio of quadratic functions satisfying all the given conditions and (0) = 5(−1)(1) (−4)(1) = 5 4 . (b) lim →∞ () = 5 lim →∞ 2 − 1 2 − 3 − 4 = 5 lim →∞ (2(2)2−(3 2) − (1 2) −2(4 ) 2) = 51 −1 −0 −0 0 = 5(1) = 5 60. = () = 23 − 4 = 3(2 − ). The -intercept is (0) = 0. The -intercepts are 0 and 2. There are sign changes at 0 and 2 (odd exponents on and 2 − ). As → ∞, () → −∞ because 3 → ∞ and 2 − → −∞. As → −∞, () → −∞ because 3 → −∞ and 2 − → ∞. Note that the graph of near = 0 flattens out (looks like = 3). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.120 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 61. = () = 4 − 6 = 4(1 − 2) = 4(1 + )(1 − ). The -intercept is (0) = 0. The -intercepts are 0, −1, and 1 [found by solving () = 0 for ]. Since 4 0 for 6= 0, doesn’t change sign at = 0. The function does change sign at = −1 and = 1. As → ±∞, () = 4(1 − 2) approaches −∞ because 4 → ∞ and (1 − 2) → −∞. 62. = () = 3( + 2)2( − 1). The -intercept is (0) = 0. The -intercepts are 0, −2, and 1. There are sign changes at 0 and 1 (odd exponents on and − 1). There is no sign change at −2. Also, () → ∞ as → ∞ because all three factors are large. And () → ∞ as → −∞ because 3 → −∞, ( + 2)2 → ∞, and ( − 1) → −∞. Note that the graph of at = 0 flattens out (looks like = −3). 63. = () = (3 − )(1 + )2(1 − )4. The -intercept is (0) = 3(1)2(1)4 = 3. The -intercepts are 3, −1, and 1. There is a sign change at 3, but not at −1 and 1. When is large positive, 3 − is negative and the other factors are positive, so lim →∞ () = −∞. When is large negative, 3 − is positive, so lim →−∞ () = ∞. 64. = () = 2(2 − 1)2( + 2) = 2( + 1)2( − 1)2( + 2). The -intercept is (0) = 0. The -intercepts are 0, −1, 1 and −2. There is a sign change at −2, but not at 0, −1, and 1. When is large positive, all the factors are positive, so lim →∞ () = ∞. When is large negative, only + 2 is negative, so lim →−∞ () = −∞. 65. (a) Since −1 ≤ sin ≤ 1 for all − 1 ≤ sin ≤ 1 for 0. As → ∞, −1 → 0 and 1 → 0, so by the Squeeze Theorem, (sin ) → 0. Thus, lim →∞ sin = 0. (b) From part (a), the horizontal asymptote is = 0. The function = (sin ) crosses the horizontal asymptote whenever sin = 0; that is, at = for every integer . Thus, the graph crosses the asymptote an infinite number of times. 66. (a) In both viewing rectangles, lim →∞ () = lim →∞ () = ∞ and lim →−∞ () = lim →−∞ () = −∞. In the larger viewing rectangle, and become less distinguishable. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.6 LIMITS AT INFINITY; HORIZONTAL ASYMPTOTES ¤ 121 (b) lim →∞ () () = lim →∞ 35 −3553 + 2 = lim →∞1 − 53 · 12 + 23 · 14 = 1 − 5 3(0) + 2 3(0) = 1 ⇒ and have the same end behavior. 67. lim →∞ 5 √ √ − 1 · 1√ 1√ = lim →∞ 1 −5(1) = √15− 0 = 5 and lim →∞ 10 − 21 2 · 1 1 = lim →∞ 10 − (21 2 ) = 102− 0 = 5. Since 102− 21 () √5√−1, we have lim →∞ () = 5 by the Squeeze Theorem. 68. (a) After minutes, 25 liters of brine with 30 g of salt per liter has been pumped into the tank, so it contains (5000 + 25) liters of water and 25 · 30 = 750 grams of salt. Therefore, the salt concentration at time will be () = 750 5000 + 25 = 30 200 + gL . (b) lim →∞ () = lim →∞ 30 200 + = lim →∞ 30 200 + = 30 0 + 1 = 30. So the salt concentration approaches that of the brine being pumped into the tank. 69. (a) lim →∞ () = lim →∞ ∗1 − −∗ = ∗(1 − 0) = ∗ (b) We graph () = 1 − −98 and () = 099∗, or in this case, () = 099. Using an intersect feature or zooming in on the point of intersection, we find that ≈ 047 s. 70. (a) = −10 and = 01 intersect at 1 ≈ 2303. If 1, then −10 01. (b) −10 01 ⇒ −10 ln 01 ⇒ −10 ln 1 10 = −10 ln 10−1 = 10 ln 10 ≈ 2303 71. Let () = 32 + 1 22 + + 1 and () = |() − 15|. Note that lim →∞ () = 3 2 and lim →∞ () = 0. We are interested in finding the -value at which () 005. From the graph, we find that ≈ 14804, so we choose = 15 (or any larger number). 72. We want to find a value of such that ⇒ 1 − 3 √2 + 1 − (−3) , or equivalently, −3 − √1−2 + 1 3 −3 + . When = 01, we graph = () = √1−2 + 1 3 , = −31, and = −29. From the graph, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.122 ¤ CHAPTER 2 LIMITS AND DERIVATIVES we find that () = −29 at about = 11283, so we choose = 12 (or any larger number). Similarly for = 005, we find that () = −295 at about = 21379, so we choose = 22 (or any larger number). 73. We want a value of such that ⇒ 1 − 3 √2 + 1 − 3 , or equivalently, 3 − √1−2 + 1 3 3 + . When = 01, we graph = () = √1−2 + 1 3 , = 31, and = 29. From the graph, we find that () = 31 at about = −8092, so we choose = −9 (or any lesser number). Similarly for = 005, we find that () = 305 at about = −18338, so we choose = −19 (or any lesser number). 74. We want to find a value of such that ⇒ √ ln 100. We graph = () = √ ln and = 100. From the graph, we find that () = 100 at about = 1382773, so we choose = 1383 (or any larger number). 75. (a) 12 00001 ⇔ 2 100001 = 10 000 ⇔ 100 ( 0) (b) If 0 is given, then 12 ⇔ 2 1 ⇔ 1√. Let = 1√. Then ⇒ √1 ⇒ 12 − 0 = 12 , so lim →∞ 12 = 0. 76. (a) 1√ 00001 ⇔ √ 100001 = 104 ⇔ 108 (b) If 0 is given, then 1√ ⇔ √ 1 ⇔ 12. Let = 12. Then ⇒ 1 2 ⇒ 1 √ − 0 = 1 √ , so lim →∞ 1 √ = 0. 77. For 0, |1 − 0| = −1. If 0 is given, then −1 ⇔ −1. Take = −1. Then ⇒ −1 ⇒ |(1) − 0| = −1 , so lim →−∞ (1) = 0. 78. Given 0, we need 0 such that ⇒ 3 . Now 3 ⇔ √3 , so take = √3 . Then = √3 ⇒ 3 , so lim →∞ 3 = ∞. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 123 79. Given 0, we need 0 such that ⇒ . Now ⇔ ln, so take = max(1 ln). (This ensures that 0.) Then = max(1 ln) ⇒ max() ≥ , so lim →∞ = ∞. 80. Definition Let be a function defined on some interval (−∞ ). Then lim →−∞ () = −∞ means that for every negative number there is a corresponding negative number such that () whenever . Now we use the definition to prove that lim →−∞ 1 + 3 = −∞. Given a negative number , we need a negative number such that ⇒ 1 + 3 . Now 1 + 3 ⇔ 3 − 1 ⇔ √3 − 1. Thus, we take = √3 − 1 and find that ⇒ 1 + 3 . This proves that lim →−∞ 1 + 3 = −∞. 81. (a) Suppose that lim →∞ () = . Then for every 0 there is a corresponding positive number such that |() − | whenever . If = 1, then ⇔ 0 1 1 ⇔ 0 1. Thus, for every 0 there is a corresponding 0 (namely 1) such that |(1) − | whenever 0 . This proves that lim →0+ (1) = = lim →∞ (). Now suppose that lim →−∞ () = . Then for every 0 there is a corresponding negative number such that |() − | whenever . If = 1, then ⇔ 1 1 0 ⇔ 1 0. Thus, for every 0 there is a corresponding 0 (namely −1) such that |(1) − | whenever − 0. This proves that lim →0− (1) = = lim →−∞ (). (b) lim →0+ sin 1 = lim →0+ sin 1 [let = ] = lim →∞ 1 sin [part (a) with = 1] = lim →∞ sin [let = ] = 0 [by Exercise 65] 2.7 Derivatives and Rates of Change 1. (a) This is just the slope of the line through two points: = ∆ ∆ = () − (3) − 3 . (b) This is the limit of the slope of the secant line as approaches : = lim →3 () − (3) − 3 . 2. The curve looks more like a line as the viewing rectangle gets smaller. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.124 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 3. (a) (i) Using Definition 1 with () = 4 − 2 and (1 3), = lim → () − () − = lim →1 (4 − 2) − 3 − 1 = lim →1 −(2 − 4 + 3) − 1 = lim →1 −( − 1)( − 3) − 1 = lim →1 (3 − ) = 3 − 1 = 2 (ii) Using Equation 2 with () = 4 − 2 and (1 3), = lim →0 ( + ) − () = lim →0 (1 + ) − (1) = lim →0 4(1 + ) −(1 + )2 − 3 = lim →0 4 + 4 − 1 − 2 − 2 − 3 = lim →0 −2+ 2 = lim →0 (−+ 2) = lim →0(− + 2) = 2 (b) An equation of the tangent line is − () = 0()( − ) ⇒ − (1) = 0(1)( − 1) ⇒ − 3 = 2( − 1), or = 2 + 1. (c) The graph of = 2 + 1 is tangent to the graph of = 4 − 2 at the point (1 3). Now zoom in toward the point (1 3) until the parabola and the tangent line are indistiguishable. 4. (a) (i) Using Definition 1 with () = − 3 and (1 0), = lim →1 () − 0 − 1 = lim →1 − 3 − 1 = lim →1 (1 − 2) − 1 = lim →1 (1 + )(1 − ) − 1 = lim →1 [−(1 + )] = −1(2) = −2 (ii) Using Equation 2 with () = − 3 and (1 0), = lim →0 ( + ) − () = lim →0 (1 + ) − (1) = lim →0 (1 + ) − (1 + )3 − 0 = lim →0 1 + − (1 + 3 + 32 + 3) = lim →0 −3 − 32 − 2 = lim →0 (−2 −3 − 2) = lim →0 (−2 − 3 − 2) = −2 (b) An equation of the tangent line is − () = 0()( − ) ⇒ − (1) = 0(1)( − 1) ⇒ − 0 = −2( − 1), or = −2 + 2. (c) The graph of = −2 + 2 is tangent to the graph of = − 3 at the point (1 0). Now zoom in toward the point (1 0) until the cubic and the tangent line are indistinguishable. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 125 5. Using (1) with () = 4 − 32 and (2 −4) [we could also use (2)], = lim → () − () − = lim →2 4 − 32− (−4) − 2 = lim →2 −32 + 4 + 4 − 2 = lim →2 (−3 − 2)( − 2) − 2 = lim →2 (−3 − 2) = −3(2) − 2 = −8 Tangent line: − (−4) = −8( − 2) ⇔ + 4 = −8 + 16 ⇔ = −8 + 12. 6. Using (2) with () = 3 − 3 + 1 and (2 3), = lim →0 ( + ) − () = lim →0 (2 + ) − (2) = lim →0 (2 + )3 − 3(2 + ) + 1 − 3 = lim →0 8 + 12 + 62 + 3 − 6 − 3 − 2 = lim →0 9 + 62 + 3 = lim →0 (9 + 6 + 2) = lim →0 (9 + 6 + 2) = 9 Tangent line: − 3 = 9( − 2) ⇔ − 3 = 9 − 18 ⇔ = 9 − 15 7. Using (1), = lim →1 √ − √1 − 1 = lim →1 (√ − 1)(√ + 1) ( − 1)(√ + 1) = lim →1 ( − 1)( −√1 + 1) = lim →1 √1+ 1 = 12. Tangent line: − 1 = 1 2( − 1) ⇔ = 1 2 + 1 2 8. Using (1) with () = 2 + 1 + 2 and (1 1), = lim → () − () − = lim →1 2 + 1 + 2 − 1 − 1 = lim →1 2 + 1 − ( + 2) + 2 − 1 = lim →1 − 1 ( − 1)( + 2) = lim →1 1 + 2 = 1 1 + 2 = 1 3 Tangent line: − 1 = 1 3( − 1) ⇔ − 1 = 1 3 − 1 3 ⇔ = 1 3 + 2 3 9. (a) Using (2) with = () = 3 + 42 − 23, = lim →0 ( + ) − () = lim →0 3 + 4( + )2 − 2( +)3 − (3 + 42 − 23) = lim →0 3 + 4(2 + 2 + 2) − 2(3 + 32 + 32 + 3) − 3 − 42 + 23 = lim →0 3 + 42 + 8 + 42 − 23 − 62 − 62 − 23 − 3 − 42 + 23 = lim →0 8 + 42 − 62 − 62 − 23 = lim →0 (8 + 4 − 62 − 6 − 22) = lim →0 (8 + 4 − 62 − 6 − 22) = 8 − 62 (b) At (1 5): = 8(1) − 6(1)2 = 2, so an equation of the tangent line is − 5 = 2( − 1) ⇔ = 2 + 3. At (2 3): = 8(2) − 6(2)2 = −8, so an equation of the tangent line is − 3 = −8( − 2) ⇔ = −8 + 19. (c) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.126 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 10. (a) Using (1), = lim → 1 √ − 1 √ − = lim → √ − √ √ − = lim → (√ − √ ) (√ + √ ) √ ( − ) (√ + √ ) = lim → √ ( −−) (√ + √ ) = lim → −1 √(√ + √ ) = −1 √2 (2√ ) = − 1 232 or − 1 2 −32 [ 0] (b) At (1 1): = − 1 2, so an equation of the tangent line is − 1 = − 1 2( − 1) ⇔ = − 1 2 + 3 2. At 4 1 2: = − 16 1 , so an equation of the tangent line is − 1 2 = − 16 1 ( − 4) ⇔ = − 16 1 + 3 4. (c) 11. (a) The particle is moving to the right when is increasing; that is, on the intervals (0 1) and (4 6). The particle is moving to the left when is decreasing; that is, on the interval (2 3). The particle is standing still when is constant; that is, on the intervals (1 2) and (3 4). (b) The velocity of the particle is equal to the slope of the tangent line of the graph. Note that there is no slope at the corner points on the graph. On the interval (0 1) the slope is 3 − 0 1 − 0 = 3. On the interval (2 3), the slope is 1 − 3 3 − 2 = −2. On the interval (4 6), the slope is 3 − 1 6 − 4 = 1. 12. (a) Runner A runs the entire 100-meter race at the same velocity since the slope of the position function is constant. Runner B starts the race at a slower velocity than runner A, but finishes the race at a faster velocity. (b) The distance between the runners is the greatest at the time when the largest vertical line segment fits between the two graphs—this appears to be somewhere between 9 and 10 seconds. (c) The runners had the same velocity when the slopes of their respective position functions are equal—this also appears to be at about 95 s. Note that the answers for parts (b) and (c) must be the same for these graphs because as soon as the velocity for runner B overtakes the velocity for runner A, the distance between the runners starts to decrease. 13. Let () = 40 − 162. (2) = lim →2 () − (2) − 2 = lim →2 40 − 162 − 16 − 2 = lim →2 −162 + 40 − 16 − 2 = lim →2 −822 − 5 + 2 − 2 = lim →2 −8( − 2)(2 − 1) − 2 = −8 lim →2 (2 − 1) = −8(3) = −24 Thus, the instantaneous velocity when = 2 is −24 fts. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 127 14. (a) Let () = 10 − 1862. (1) = lim →0 (1 + ) − (1) = lim →0 10(1 + ) − 186(1 + )2 − (10 − 186) = lim →0 10 + 10 − 186(1 + 2 + 2) − 10 + 186 = lim →0 10 + 10 − 186 − 372 − 1862 − 10 + 186 = lim →0 628 − 1862 = lim →0(628 − 186) = 628 The velocity of the rock after one second is 628 ms. (b) () = lim →0 ( + ) − () = lim →0 10( + ) − 186( + )2 − (10 − 1862) = lim →0 10 + 10 − 186(2 + 2 + 2) − 10 + 1862 = lim →0 10 + 10 − 1862 − 372 − 1862 − 10 + 1862 = lim →0 10 − 372 − 1862 = lim →0 (10 − 372 − 186) = lim →0(10 − 372 − 186) = 10 − 372 The velocity of the rock when = is (10 − 372) ms (c) The rock will hit the surface when = 0 ⇔ 10 − 1862 = 0 ⇔ (10 − 186) = 0 ⇔ = 0 or 186 = 10. The rock hits the surface when = 10186 ≈ 54 s. (d) The velocity of the rock when it hits the surface is 110 86 = 10 − 372 110 86 = 10 − 20 = −10 ms. 15. () = lim →0 ( + ) − () = lim →0 1 ( + )2 − 1 2 = lim →0 2 − ( + )2 2( + )2 = lim →0 2 − (22(+ 2 + )+2 2) = lim →0 −(2 + 2) 2( + )2 = lim →0 −2(2 (++))2 = lim →0 −2(2 (++))2 = −2 ·22 = −32 ms So (1) = −2 13 = −2 ms, (2) = −232 = −1 4ms, and (3) = −332 = −27 2 ms. 16. (a) The average velocity between times and + is ( + ) − () ( + ) − = 12 ( + )2 − 6( + ) + 23 − 1 22 − 6 + 23 = 12 2 + + 1 22 − 6 − 6 + 23 − 1 22 + 6 − 23 = + 1 22 − 6 = + 1 2 − 6 = + 1 2 − 6 fts (i) [4 8]: = 4, = 8 − 4 = 4, so the average velocity is 4 + 1 2(4) − 6 = 0 fts. (ii) [6 8]: = 6, = 8 − 6 = 2, so the average velocity is 6 + 1 2(2) − 6 = 1 fts. (iii) [8 10]: = 8, = 10 − 8 = 2, so the average velocity is 8 + 1 2(2) − 6 = 3 fts. (iv) [8 12]: = 8, = 12 − 8 = 4, so the average velocity is 8 + 1 2(4) − 6 = 4 fts. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.128 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (b) () = lim →0 ( + ) − () = lim →0 + 1 2 − 6 = − 6, so (8) = 2 fts. (c) 17. 0(0) is the only negative value. The slope at = 4 is smaller than the slope at = 2 and both are smaller than the slope at = −2. Thus, 0(0) 0 0(4) 0(2) 0(−2). 18. (a) On [20 60]: (60) − (20) 60 − 20 = 700 − 300 40 = 400 40 = 10 (b) Pick any interval that has the same -value at its endpoints. [0 57] is such an interval since (0) = 600 and (57) = 600. (c) On [40 60]: (60) − (40) 60 − 40 = 700 − 200 20 = 500 20 = 25 On [40 70]: (70) − (40) 70 − 40 = 900 − 200 30 = 700 30 = 23 1 3 Since 25 23 1 3, the average rate of change on [40 60] is larger. (d) (40) − (10) 40 − 10 = 200 − 400 30 = −200 30 = −6 2 3 This value represents the slope of the line segment from (10 (10)) to (40 (40)). 19. (a) The tangent line at = 50 appears to pass through the points (43 200) and (60 640), so 0(50) ≈ 640 − 200 60 − 43 = 440 17 ≈ 26. (b) The tangent line at = 10 is steeper than the tangent line at = 30, so it is larger in magnitude, but less in numerical value, that is, 0(10) 0(30). (c) The slope of the tangent line at = 60, 0(60), is greater than the slope of the line through (40 (40)) and (80 (80)). So yes, 0(60) (80) − (40) 80 − 40 . 20. Since (5) = −3, the point (5 −3) is on the graph of . Since 0(5) = 4, the slope of the tangent line at = 5 is 4. Using the point-slope form of a line gives us − (−3) = 4( − 5), or = 4 − 23. 21. For the tangent line = 4 − 5: when = 2, = 4(2) − 5 = 3 and its slope is 4 (the coefficient of ). At the point of tangency, these values are shared with the curve = (); that is, (2) = 3 and 0(2) = 4. 22. Since (4 3) is on = (), (4) = 3. The slope of the tangent line between (0 2) and (4 3) is 1 4, so 0(4) = 1 4. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 129 23. We begin by drawing a curve through the origin with a slope of 3 to satisfy (0) = 0 and 0(0) = 3. Since 0(1) = 0, we will round off our figure so that there is a horizontal tangent directly over = 1. Last, we make sure that the curve has a slope of −1 as we pass over = 2. Two of the many possibilities are shown. 24. We begin by drawing a curve through the origin with a slope of 1 to satisfy (0) = 0 and 0(0) = 1. We round off our figure at = 1 to satisfy 0(1) = 0, and then pass through (2 0) with slope −1 to satisfy (2) = 0 and 0(2) = −1. We round the figure at = 3 to satisfy 0(3) = 0, and then pass through (4 0) with slope 1 to satisfy (4) = 0 and 0(4) = 1 Finally we extend the curve on both ends to satisfy lim →∞ () = ∞ and lim →−∞ () = −∞. 25. We begin by drawing a curve through (0 1) with a slope of 1 to satisfy (0) = 1 and 0(0) = 1. We round off our figure at = −2 to satisfy 0(−2) = 0. As → −5+, → ∞, so we draw a vertical asymptote at = −5. As → 5−, → 3, so we draw a dot at (5 3) [the dot could be open or closed]. 26. We begin by drawing an odd function (symmetric with respect to the origin) through the origin with slope −2 to satisfy 0(0) = −2. Now draw a curve starting at = 1 and increasing without bound as → 2− since lim →2− () = ∞. Lastly, reflect the last curve through the origin (rotate 180◦) since is an odd function. 27. Using (4) with () = 32 − 3 and = 1, 0(1) = lim →0 (1 + ) − (1) = lim →0 [3(1 + )2 −(1 + )3] − 2 = lim →0 (3 + 6 + 32) − (1 + 3 + 32 + 3) − 2 = lim →0 3 − 3 = lim →0 (3 − 2) = lim →0 (3 − 2) = 3 − 0 = 3 Tangent line: − 2 = 3( − 1) ⇔ − 2 = 3 − 3 ⇔ = 3 − 1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.130 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 28. Using (5) with () = 4 − 2 and = 1, 0(1) = lim →1 () − (1) − 1 = lim →1 (4 − 2) − (−1) − 1 = lim →1 4 − 1 − 1 = lim →1 (2 + 1)(2 − 1) − 1 = lim →1 (2 + 1)( + 1)( − 1) − 1 = lim →1 [(2 + 1)( + 1)] = 2(2) = 4 Tangent line: − (−1) = 4( − 1) ⇔ + 1 = 4 − 4 ⇔ = 4 − 5 29. (a) Using (4) with () = 5(1 + 2) and the point (2 2), we have 0(2) = lim →0 (2 + ) − (2) = lim →0 5(2 + ) 1 + (2 + )2 − 2 = lim →0 5 + 10 2 + 4 + 5 − 2 = lim →0 5 + 10 − 2(2 + 4 + 5) 2 + 4 + 5 = lim →0 −22 − 3 (2 + 4 + 5) = lim →0 ((2−+ 4 2 −+ 5) 3) = lim →0 2−+ 4 2 −+ 5 3 = −53 So an equation of the tangent line at (2 2) is − 2 = − 3 5( − 2) or = − 3 5 + 16 5 . (b) 30. (a) Using (4) with () = 42 − 3, we have 0() = lim →0 ( + ) − () = lim →0 [4( + )2 − ( +)3] − (42 − 3) = lim →0 42 + 8 + 42 − (3 + 32 + 32 + 3) − 42 + 3 = lim →0 8 + 42 − 32 − 32 − 3 = lim →0 (8 + 4 − 32 − 3 − 2) = lim →0 (8 + 4 − 32 − 3 − 2) = 8 − 32 At the point (2 8), 0(2) = 16 − 12 = 4, and an equation of the tangent line is − 8 = 4( − 2), or = 4. At the point (3 9), 0(3) = 24 − 27 = −3, and an equation of the tangent line is − 9 = −3( − 3), or = −3 + 18 (b) 31. Use (4) with () = 32 − 4 + 1. 0() = lim →0 ( + ) − () = lim →0 [3( + )2 − 4( + ) + 1] − (32 − 4 + 1)] = lim →0 32 + 6 + 32 − 4 − 4 + 1 − 32 + 4 − 1 = lim →0 6 + 32 − 4 = lim →0 (6 + 3 − 4) = lim →0(6 + 3 − 4) = 6 − 4 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 131 32. Use (4) with () = 23 + . 0() = lim →0 ( + ) − () = lim →0 [2( + )3 + ( + )] − (23 + ) = lim →0 23 + 62 + 62 + 23 + + − 23 − = lim →0 62 + 62 + 23 + = lim →0 (62 + 6 + 22 + 1) = lim →0(62 + 6 + 22 + 1) = 62 + 1 33. Use (4) with () = (2 + 1)( + 3). 0() = lim →0 ( + ) − () = lim →0 2( + ) + 1 ( + ) + 3 − 2 + 1 + 3 = lim →0 (2 + 2 + 1)( + 3) − (2 + 1)( + + 3) ( + + 3)( + 3) = lim →0 (22 + 6 + 2 + 6 + + 3) − (22 + 2 + 6 + + + 3) ( + + 3)( + 3) = lim →0 5 ( + + 3)( + 3) = lim →0 ( + + 3)( 5 + 3) = ( + 3) 5 2 34. Use (4) with () = −2 = 12. 0() = lim →0 ( + ) − () = lim →0 1 ( + )2 − 1 2 = lim →0 2 − ( + )2 2( + )2 = lim →0 2 − (2 + 2 + 2) 2( + )2 = lim →0 −22 ( +−)22 = lim →0 (−2(2+−))2 = lim →0 −2 − 2( + )2 = −2 2(2) = −2 3 35. Use (4) with () = √1 − 2. 0() = lim →0 ( + ) − () = lim →0 1 − 2( + ) − √1 − 2 = lim →0 1 − 2( + ) − √1 − 2 · 1 − 2( + ) + √1 − 2 1 − 2( + ) + √1 − 2 = lim →0 1 − 2( + ) 2 − √1 − 2 2 1 − 2( + ) + √1 − 2 = lim →0 (11−−22(− +2)) + − (1√−1 −22) = lim →0 −2 1 − 2( + ) + √1 − 2 = lim →0 1 − 2( +−2) + √1 − 2 = −2 √1 − 2 + √1 − 2 = −2 2 √1 − 2 = −1 √1 − 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.132 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 36. Use (4) with () = √14− . 0() = lim →0 ( + ) − () = lim →0 4 1 − ( + ) − 4 √1 − = 4 lim →0 √1 − − √1 − − √1 − − √1 − = 4 lim →0 √1 − − √1 − − √1 − − √1 − = 4 lim →0 √1 − − √1 − − √1 − − √1 − · √1 − + √1 − − √1 − + √1 − − = 4 lim →0 √1 − (−√1−√1)−2 −((√√11−−+−√1)2− − ) = 4 lim →0 (1 − ) − (1 − − ) √1 − − √1 − (√1 − + √1 − − ) = 4 lim →0 √1 − − √1 − (√1 − + √1 − − ) = 4 lim →0 1 √1 − − √1 − (√1 − + √1 − − ) = 4 · √1 − √1 − (√11 − + √1 − ) = 4 (1 − )(2√1 − ) = 2 (1 − )1(1 − )12 = 2 (1 − )32 37. By (4), lim →0 √9 + − 3 = 0(9), where () = √ and = 9. 38. By (4), lim →0 −2+ − −2 = 0(−2), where () = and = −2. 39. By Equation 5, lim →2 6 − 64 − 2 = 0(2), where () = 6 and = 2. 40. By Equation 5, lim →14 1 − 4 − 1 4 = 0(4), where () = 1 and = 1 4. 41. By (4), lim →0 cos( + ) + 1 = 0(), where () = cos and = . Or: By (4), lim →0 cos( + ) + 1 = 0(0), where () = cos( + ) and = 0. 42. By Equation 5, lim →6 sin − 1 2 − 6 = 0 6 , where () = sin and = 6 . 43. (4) = 0(4) = lim →0 (4 + ) − (4) = lim →0 80(4 + ) − 6(4 + )2 − 80(4) − 6(4)2 = lim →0 (320 + 80 − 96 − 48 − 62) − (320 − 96) = lim →0 32 − 62 = lim →0 (32 − 6) = lim →0(32 − 6) = 32 m/s The speed when = 4 is |32| = 32 ms. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 133 44. (4) = 0(4) = lim →0 (4 + ) − (4) = lim →0 10 + 4 +45 + 1 − 10 + 4 + 1 45 = lim →0 45 5 + − 9 = lim →0 45 − 9(5 + ) (5 + ) = lim →0 (5 + −9) = lim →0 5 + −9 = −95 m/s. The speed when = 4 is − 9 5 = 9 5 ms. 45. The sketch shows the graph for a room temperature of 72◦ and a refrigerator temperature of 38◦. The initial rate of change is greater in magnitude than the rate of change after an hour. 46. The slope of the tangent (that is, the rate of change of temperature with respect to time) at = 1 h seems to be about 75 − 168 132 − 0 ≈ −07 ◦Fmin. 47. (a) (i) [10 20]: (2) − (1) 2 − 1 = 018 − 033 1 = −015 mg/mL h (ii) [15 20]: (2) − (15) 2 − 15 = 018 − 024 05 = −006 05 = −012 mg/mL h (iii) [20 25]: (25) − (2) 25 − 2 = 012 − 018 05 = −006 05 = −012 mg/mL h (iv) [20 30]: (3) − (2) 3 − 2 = 007 − 018 1 = −011 mg/mL h (b) We estimate the instantaneous rate of change at = 2 by averaging the average rates of change for [15 20] and [20 25]: −012 + (−012) 2 = −012 mg/mL h . After 2 hours, the BAC is decreasing at a rate of 012 (mgmL)h. 48. (a) (i) [2006 2008]: (2008) − (2006) 2008 − 2006 = 16,680 − 12,440 2 = 4240 2 = 2120 locationsyear (ii) [2008 2010]: (2010) − (2008) 2010 − 2008 = 16,858 − 16,680 2 = 178 2 = 89 locationsyear. The rate of growth decreased over the period from 2006 to 2010. (b) [2010 2012]: (2012) − (2010) 2012 − 2010 = 18,066 − 16,858 2 = 1208 2 = 604 locationsyear. Using that value and the value from part (a)(ii), we have 89 + 604 2 = 693 2 = 3465 locationsyear. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.134 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (c) The tangent segment has endpoints (2008 16,250) and (2012 17,500). An estimate of the instantaneous rate of growth in 2010 is 17,500 − 16,250 2012 − 2008 = 1250 4 = 3125 locations/year. 49. (a) [1990 2005]: 84,077 − 66,533 2005 − 1990 = 17,544 15 = 11696 thousands of barrels per day per year. This means that oil consumption rose by an average of 11696 thousands of barrels per day each year from 1990 to 2005. (b) [1995 2000]: 76,784 − 70,099 2000 − 1995 = 6685 5 = 1337 [2000 2005]: 84,077 − 76,784 2005 − 2000 = 7293 5 = 14586 An estimate of the instantaneous rate of change in 2000 is 1 2 (1337 + 14586) = 13978 thousands of barrels per day per year. 50. (a) (i) [4 11]: (11) − (4) 11 − 4 = 94 − 53 7 = −436 7 ≈ −623 RNA copies day mL (ii) [8 11]: (11) − (8) 11 − 8 = 94 − 18 3 = −86 3 ≈ −287 RNA copiesmL day (iii) [11 15]: (15) − (11) 15 − 11 = 52 − 94 4 = −42 4 = −105 RNA copies day mL (iv) [11 22]: (22) − (11) 22 − 11 = 36 − 94 11 = −58 11 ≈ −053 RNA copiesmL day (b) An estimate of 0(11) is the average of the answers from part (a)(ii) and (iii). 0(11) ≈ 1 2 [−287 + (−105)] = −196 RNA copiesmL day . 0(11) measures the instantaneous rate of change of patient 303’s viral load 11 days after ABT-538 treatment began. 51. (a) (i) ∆ ∆ = (105) − (100) 105 − 100 = 660125 − 6500 5 = $2025unit. (ii) ∆ ∆ = (101) − (100) 101 − 100 = 652005 − 6500 1 = $2005unit. (b) (100 + ) − (100) = 5000 + 10(100 + ) + 005(100 + )2 − 6500 = 20 + 0052 = 20 + 005, 6= 0 So the instantaneous rate of change is lim →0 (100 + ) − (100) = lim →0(20 + 005) = $20unit. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.7 DERIVATIVES AND RATES OF CHANGE ¤ 135 52. ∆ = ( + ) − () = 100,000 1 − +602 − 100,000 1 − 60 2 = 100,000 1 − 30 + + (3600 + )2 − 1 − 30 + 3600 2 = 100,000−30 + 3600 2 + 3600 2 = 100,000 3600 (−120 + 2 + ) = 250 9 (−120 + 2 + ) Dividing ∆ by and then letting → 0, we see that the instantaneous rate of change is 500 9 ( − 60) galmin. Flow rate (galmin) Water remaining () (gal) 0 −33333 100 000 10 −27777 69 4444 20 −22222 44 4444 30 −16666 25 000 40 −11111 11 1111 50 − 5555 2 7777 60 0 0 The magnitude of the flow rate is greatest at the beginning and gradually decreases to 0. 53. (a) 0() is the rate of change of the production cost with respect to the number of ounces of gold produced. Its units are dollars per ounce. (b) After 800 ounces of gold have been produced, the rate at which the production cost is increasing is $17ounce. So the cost of producing the 800th (or 801st) ounce is about $17. (c) In the short term, the values of 0() will decrease because more efficient use is made of start-up costs as increases. But eventually 0() might increase due to large-scale operations. 54. (a) 0(5) is the rate of growth of the bacteria population when = 5 hours. Its units are bacteria per hour. (b) With unlimited space and nutrients, 0 should increase as increases; so 0(5) 0(10). If the supply of nutrients is limited, the growth rate slows down at some point in time, and the opposite may be true. 55. (a) 0(58) is the rate at which the daily heating cost changes with respect to temperature when the outside temperature is 58 ◦F. The units are dollars ◦F. (b) If the outside temperature increases, the building should require less heating, so we would expect 0(58) to be negative. 56. (a) 0(8) is the rate of change of the quantity of coffee sold with respect to the price per pound when the price is $8 per pound. The units for 0(8) are pounds(dollarspound). (b) 0(8) is negative since the quantity of coffee sold will decrease as the price charged for it increases. People are generally less willing to buy a product when its price increases. 57. (a) 0() is the rate at which the oxygen solubility changes with respect to the water temperature. Its units are (mgL)◦C. (b) For = 16◦C, it appears that the tangent line to the curve goes through the points (0 14) and (32 6). So 0(16) ≈ 6 − 14 32 − 0 = − 8 32 = −025 (mgL)◦C. This means that as the temperature increases past 16◦C, the oxygen solubility is decreasing at a rate of 025 (mgL)◦C. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.136 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 58. (a) 0() is the rate of change of the maximum sustainable speed of Coho salmon with respect to the temperature. Its units are (cms)◦C. (b) For = 15◦C, it appears the tangent line to the curve goes through the points (10 25) and (20 32). So 0(15) ≈ 32 − 25 20 − 10 = 07 (cms)◦C. This tells us that at = 15◦C, the maximum sustainable speed of Coho salmon is changing at a rate of 0.7 (cms)◦C. In a similar fashion for = 25◦C, we can use the points (20 35) and (25 25) to obtain 0(25) ≈ 25 − 35 25 − 20 = −2 (cms)◦C. As it gets warmer than 20◦C, the maximum sustainable speed decreases rapidly. 59. Since () = sin(1) when 6= 0 and (0) = 0, we have 0(0) = lim →0 (0 + ) − (0) = lim →0 sin(1) − 0 = lim →0 sin(1). This limit does not exist since sin(1) takes the values −1 and 1 on any interval containing 0. (Compare with Example 2.2.4.) 60. Since () = 2 sin(1) when 6= 0 and (0) = 0, we have 0(0) = lim →0 (0 + ) − (0) = lim →0 2 sin(1) − 0 = lim →0 sin(1). Since −1 ≤ sin 1 ≤ 1, we have − || ≤ || sin 1 ≤ || ⇒ − || ≤ sin 1 ≤ ||. Because lim →0 (− ||) = 0 and lim →0 || = 0, we know that lim →0 sin 1 = 0 by the Squeeze Theorem. Thus, 0(0) = 0. 61. (a) The slope at the origin appears to be 1. (b) The slope at the origin still appears to be 1. (c) Yes, the slope at the origin now appears to be 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 137 2.8 The Derivative as a Function 1. It appears that is an odd function, so 0 will be an even function—that is, 0(−) = 0(). (a) 0(−3) ≈ −02 (b) 0(−2) ≈ 0 (c) 0(−1) ≈ 1 (d) 0(0) ≈ 2 (e) 0(1) ≈ 1 (f) 0(2) ≈ 0 (g) 0(3) ≈ −02 2. Your answers may vary depending on your estimates. (a) Note: By estimating the slopes of tangent lines on the graph of , it appears that 0(0) ≈ 6. (b) 0(1) ≈ 0 (c) 0(2) ≈ −15 (d) 0(3) ≈ −13 (e) 0(4) ≈ −08 (f) 0(5) ≈ −03 (g) 0(6) ≈ 0 (h) 0(7) ≈ 02 3. (a)0 = II, since from left to right, the slopes of the tangents to graph (a) start out negative, become 0, then positive, then 0, then negative again. The actual function values in graph II follow the same pattern. (b)0 = IV, since from left to right, the slopes of the tangents to graph (b) start out at a fixed positive quantity, then suddenly become negative, then positive again. The discontinuities in graph IV indicate sudden changes in the slopes of the tangents. (c)0 = I, since the slopes of the tangents to graph (c) are negative for 0 and positive for 0, as are the function values of graph I. (d)0 = III, since from left to right, the slopes of the tangents to graph (d) are positive, then 0, then negative, then 0, then positive, then 0, then negative again, and the function values in graph III follow the same pattern. Hints for Exercises 4 –11: First plot -intercepts on the graph of 0 for any horizontal tangents on the graph of . Look for any corners on the graph of — there will be a discontinuity on the graph of 0. On any interval where has a tangent with positive (or negative) slope, the graph of 0 will be positive (or negative). If the graph of the function is linear, the graph of 0 will be a horizontal line. 4. 5. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.138 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 6. 7. 9. 9. 10. 11. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 139 12. The slopes of the tangent lines on the graph of = () are always positive, so the -values of = 0() are always positive. These values start out relatively small and keep increasing, reaching a maximum at about = 6. Then the -values of = 0() decrease and get close to zero. The graph of 0 tells us that the yeast culture grows most rapidly after 6 hours and then the growth rate declines. 13. (a) 0() is the instantaneous rate of change of percentage of full capacity with respect to elapsed time in hours. (b) The graph of 0() tells us that the rate of change of percentage of full capacity is decreasing and approaching 0. 14. (a) 0() is the instantaneous rate of change of fuel economy with respect to speed. (b) Graphs will vary depending on estimates of 0, but will change from positive to negative at about = 50. (c) To save on gas, drive at the speed where is a maximum and 0 is 0, which is about 50 mi h. 15. It appears that there are horizontal tangents on the graph of for = 1963 and = 1971. Thus, there are zeros for those values of on the graph of 0. The derivative is negative for the years 1963 to 1971. 16. See Figure 3.3.1. 17. The slope at 0 appears to be 1 and the slope at 1 appears to be 27. As decreases, the slope gets closer to 0. Since the graphs are so similar, we might guess that 0() = . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.140 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 18. As increases toward 1, 0() decreases from very large numbers to 1. As becomes large, 0() gets closer to 0. As a guess, 0() = 12 or 0() = 1 makes sense. 19. (a) By zooming in, we estimate that 0(0) = 0, 0 1 2 = 1, 0(1) = 2, and 0(2) = 4. (b) By symmetry, 0(−) = − 0(). So 0− 1 2 = −1, 0(−1) = −2, and 0(−2) = −4. (c) It appears that 0() is twice the value of , so we guess that 0() = 2. (d) 0() = lim →0 ( + ) − () = lim →0 ( + )2 − 2 = lim →0 2 + 2 + 2 − 2 = lim →0 2+ 2 = lim →0 (2+ ) = lim →0(2 + ) = 2 20. (a) By zooming in, we estimate that 0(0) = 0, 0 1 2 ≈ 075, 0(1) ≈ 3, 0(2) ≈ 12, and 0(3) ≈ 27. (b) By symmetry, 0(−) = 0(). So 0− 1 2 ≈ 075, 0(−1) ≈ 3, 0(−2) ≈ 12, and 0(−3) ≈ 27. (c) (d) Since 0(0) = 0, it appears that 0 may have the form 0() = 2. Using 0(1) = 3, we have = 3, so 0() = 32. (e) 0() = lim →0 ( + ) − () = lim →0 ( + )3 − 3 = lim →0 (3 + 32 + 32 + 3) − 3 = lim →0 32 + 32 + 3 = lim →0 (32 + 3 + 2) = lim →0(32 + 3 + 2) = 32 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 141 21. 0() = lim →0 ( + ) − () = lim →0 [3( + ) −8] − (3 − 8) = lim →0 3 + 3 −8 − 3 + 8 = lim →0 3 = lim →0 3 = 3 Domain of = domain of 0 = R. 22. 0() = lim →0 ( + ) − () = lim →0 [( + ) +] − ( + ) = lim →0 + + − − = lim →0 = lim →0 = Domain of = domain of 0 = R. 23. 0() = lim →0 ( + ) − () = lim →0 25( + )2 + 6( + ) − 252 + 6 = lim →0 25(2 + 2 + 2) + 6 + 6 − 252 − 6 = lim →0 252 + 5 + 252 + 6 − 252 = lim →0 5 + 252 + 6 = lim →0 (5 + 25 + 6) = lim →0 (5 + 25 + 6) = 5 + 6 Domain of = domain of 0 = R. 24. 0() = lim →0 ( + ) − () = lim →0 4 + 8( + ) − 5( + )2 − (4 + 8 − 52) = lim →0 4 + 8 + 8 − 5(2 + 2 + 2) − 4 − 8 + 52 = lim →0 8 − 52 − 10 − 52 + 52 = lim →0 8 − 10 − 52 = lim →0 (8 − 10 − 5) = lim →0 (8 − 10 − 5) = 8 − 10 Domain of = domain of 0 = R. 25. 0() = lim →0 ( + ) − () = lim →0 [( + )2 − 2( +)3] − (2 − 23) = lim →0 2 + 2 + 2 − 23 − 62 − 62 − 23 − 2 + 23 = lim →0 2 + 2 − 62 − 62 − 23 = lim →0 (2 + − 62 − 6 − 22) = lim →0 (2 + − 62 − 6 − 22) = 2 − 62 Domain of = domain of 0 = R. 26. 0() = lim →0 ( + ) − () = lim →0 1 √ + − 1 √ = lim →0 √ − √ + √ + √ = lim →0 √√− +√+√ · √√ + + √ √ + + = lim →0 − ( + ) √ + √ √ + √ + = lim →0 √ + √−√ + √ + = lim →0 √ + √ −√1 + √ + = −1 √ √ √ + √ = −1 2 √ = − 1 232 Domain of = domain of 0 = (0 ∞). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.142 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 27. 0() = lim →0 ( + ) − () = lim →0 9 − ( + ) − √9 − 9 9 − − ( ( + + ) + ) + √ √9 9 − − = lim →0 [9 − ( + )] − (9 − ) 9 − ( + ) + √9 − = lim →0 9 − ( +−) + √9 − = lim →0 −1 9 − ( + ) + √9 − = −1 2√9 − Domain of = (−∞ 9], domain of 0 = (−∞ 9). 28. 0() = lim →0 ( + ) − () = lim →0 ( + )2 − 1 2( + ) − 3 − 2 − 1 2 − 3 = lim →0 [( + )2 − 1](2 − 3) − [2( + ) − 3](2 − 1) [2( + ) − 3](2 − 3) = lim →0 (2 + 2 + 2 − 1)(2 − 3) − (2 + 2 − 3)(2 − 1) [2( + ) − 3](2 − 3) = lim →0 (23 + 42 + 22 − 2 − 32 − 6 − 32 + 3) − (23 + 22 − 32 − 2 − 2 + 3) (2 + 2 − 3)(2 − 3) = lim →0 42 + 22 − 6 − 32 − 22 + 2 (2 + 2 − 3)(2 − 3) = lim →0 (2(22+ 2 + 2 − − 6 3)(2 −3− 3) + 2) = lim →0 22 + 2 − 6 − 3 + 2 (2 + 2 − 3)(2 − 3) = 22 − 6 + 2 (2 − 3)2 Domain of = domain of 0 = (−∞ 3 2) ∪ ( 3 2 ∞). 29. 0() = lim →0 ( + ) − () = lim →0 1 − 2( + ) 3 + ( + ) − 1 − 2 3 + = lim →0 [1 − 2( + )](3 + ) − [3 + ( + )](1 − 2) [3 + ( + )](3 + ) = lim →0 3 + − 6 − 22 − 6 − 2 − (3 − 6 + − 22 + − 2) [3 + ( + )](3 + ) = lim →0 (3 +−6+ −)(3 + ) = lim →0 −7 (3 + + )(3 + ) = lim →0 (3 + +−7)(3 + ) = (3 + −7)2 Domain of = domain of 0 = (−∞ −3) ∪ (−3 ∞). 30. 0() = lim →0 ( + ) − () = lim →0 ( + )32 − 32 = lim →0 [( + )32[(− +32)][( 32++3)32]2 + 32] = lim →0 ( + )3 − 3 [( + )32 + 32] = lim →0 3 + 3 [(2++ 3 )3 2 2++332]− 3 = lim →0 [(3+2 + 3 )3 2 ++322] = lim →0 32 + 3 + 2 ( + )32 + 32 = 32 232 = 32 12 Domain of = domain of 0 = [0 ∞). Strictly speaking, the domain of 0 is (0 ∞) because the limit that defines 0(0) does °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 143 not exist (as a two-sided limit). But the right-hand derivative (in the sense of Exercise 64) does exist at 0, so in that sense one could regard the domain of 0 to be [0 ∞). 31. 0() = lim →0 ( + ) − () = lim →0 ( + )4 − 4 = lim →0 4 + 43 + 622+ 43 + 4 − 4 = lim →0 43 + 622 + 43 + 4 = lim →0 43 + 62 + 42 + 3 = 43 Domain of = domain of 0 = R. 32. (a) (b) Note that the third graph in part (a) has small negative values for its slope, 0; but as → 6−, 0 → −∞. See the graph in part (d). (c) 0() = lim →0 ( + ) − () = lim →0 6 − ( + ) − √6 − 6 6 − − ( ( + + ) + ) + √ √6 6 − − = lim →0 [6 − ( + )] − (6 − ) 6 − ( + ) + √6 − = lim →0 √6 − −−+ √6 − = lim →0 −1 √6 − − + √6 − = −1 2 √6 − Domain of = (−∞ 6], domain of 0 = (−∞ 6). (d) 33. (a) 0() = lim →0 ( + ) − () = lim →0 [( + )4 + 2( + )] − (4 + 2) = lim →0 4 + 43 + 622 + 43 + 4 + 2 + 2 − 4 − 2 = lim →0 43 + 622 + 43 + 4 + 2 = lim →0 (43 + 62 + 4 2 + 3 + 2) = lim →0 (43 + 62 + 42 + 3 + 2) = 43 + 2 (b) Notice that 0() = 0 when has a horizontal tangent, 0() is positive when the tangents have positive slope, and 0() is negative when the tangents have negative slope. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.144 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 34. (a) 0() = lim →0 ( + ) − () = lim →0 [( + ) + 1( + )] − ( + 1) = lim →0 ( + )2 + 1 + − 2 + 1 = lim →0 [( + )2 + 1] − ( + )(2 + 1) ( + ) = lim →0 (3 + 22 + 2+(+) −)(3 + + 2 + ) = lim →0 2 + 2 − ( + ) = lim →0 (2(++)− 1) = lim →0 2(++)− 1 = 2−2 1, or 1 − 12 (b) Notice that 0() = 0 when has a horizontal tangent, 0() is positive when the tangents have positive slope, and 0() is negative when the tangents have negative slope. Both functions are discontinuous at = 0. 35. (a) 0() is the rate at which the unemployment rate is changing with respect to time. Its units are percent unemployed per year. (b) To find 0(), we use lim →0 ( + ) − () ≈ ( + ) − () for small values of . For 2003: 0(2003) ≈ (2004) − (2003) 2004 − 2003 = 55 − 60 1 = −05 For 2004: We estimate 0(2004) by using = −1 and = 1, and then average the two results to obtain a final estimate. = −1 ⇒ 0(2004) ≈ (2003) − (2004) 2003 − 2004 = 60 − 55 −1 = −05; = 1 ⇒ 0(2004) ≈ (2005) − (2004) 2005 − 2004 = 51 − 55 1 = −04. So we estimate that 0(2004) ≈ 1 2[−05 + (−04)] = −045. 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 0() −050 −045 −045 −025 060 235 190 −020 −075 −080 36. (a) 0() is the rate at which the number of minimally invasive cosmetic surgery procedures performed in the United States is changing with respect to time. Its units are thousands of surgeries per year. (b) To find 0(), we use lim →0 ( + ) − () ≈ ( + ) − () for small values of . For 2000: 0(2000) ≈ (2002) − (2000) 2002 − 2000 = 4897 − 5500 2 = −3015 For 2002: We estimate 0(2002) by using = −2 and = 2, and then average the two results to obtain a final estimate. = −2 ⇒ 0(2002) ≈ (2000) − (2002) 2000 − 2002 = 5500 − 4897 −2 = −3015 = 2 ⇒ 0(2002) ≈ (2004) − (2002) 2004 − 2002 = 7470 − 4897 2 = 12865 So we estimate that 0(2002) ≈ 1 2[−3015 + 12865] = 4925. 2000 2002 2004 2006 2008 2010 2012 0() −3015 4925 106025 85675 60575 5345 737 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 145 (c) (d) We could get more accurate values for 0() by obtaining data for more values of . 37. As in Exercise 35, we use one-sided difference quotients for the first and last values, and average two difference quotients for all other values. 14 21 28 35 42 49 () 41 54 64 72 78 83 0() 13 7 23 14 18 14 14 14 11 14 5 7 38. As in Exercise 35, we use one-sided difference quotients for the first and last values, and average two difference quotients for all other values. The units for 0() are grams per degree (g◦C). 155 177 200 224 244 () 372 310 198 97 −98 0() −282 −387 −453 −673 −975 39. (a) is the rate at which the percentage of the city’s electrical power produced by solar panels changes with respect to time , measured in percentage points per year. (b) 2 years after January 1, 2000 (January 1, 2002), the percentage of electrical power produced by solar panels was increasing at a rate of 3.5 percentage points per year. 40. is the rate at which the number of people who travel by car to another state for a vacation changes with respect to the price of gasoline. If the price of gasoline goes up, we would expect fewer people to travel, so we would expect to be negative. 41. is not differentiable at = −4, because the graph has a corner there, and at = 0, because there is a discontinuity there. 42. is not differentiable at = −1, because there is a discontinuity there, and at = 2, because the graph has a corner there. 43. is not differentiable at = 1, because is not defined there, and at = 5, because the graph has a vertical tangent there. 44. is not differentiable at = −2 and = 3, because the graph has corners there, and at = 1, because there is a discontinuity there. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.146 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 45. As we zoom in toward (−1 0), the curve appears more and more like a straight line, so () = + || is differentiable at = −1. But no matter how much we zoom in toward the origin, the curve doesn’t straighten out—we can’t eliminate the sharp point (a cusp). So is not differentiable at = 0. 46. As we zoom in toward (0 1), the curve appears more and more like a straight line, so is differentiable at = 0. But no matter how much we zoom in toward (1 0) or (−1 0), the curve doesn’t straighten out—we can’t eliminate the sharp point (a cusp). So is not differentiable at = ±1. 47. Call the curve with the positive -intercept and the other curve . Notice that has a maximum (horizontal tangent) at = 0, but 6= 0, so cannot be the derivative of . Also notice that where is positive, is increasing. Thus, = and = 0. Now 0(−1) is negative since 0 is below the -axis there and 00(1) is positive since is concave upward at = 1. Therefore, 00(1) is greater than 0(−1). 48. Call the curve with the smallest positive -intercept and the other curve . Notice that where is positive in the first quadrant, is increasing. Thus, = and = 0. Now 0(−1) is positive since 0 is above the -axis there and 00(1) appears to be zero since has an inflection point at = 1. Therefore, 0(1) is greater than 00(−1). 49. = , = 0, = 00. We can see this because where has a horizontal tangent, = 0, and where has a horizontal tangent, = 0. We can immediately see that can be neither nor 0, since at the points where has a horizontal tangent, neither nor is equal to 0. 50. Where has horizontal tangents, only is 0, so 0 = . has negative tangents for 0 and is the only graph that is negative for 0, so 0 = . has positive tangents on R (except at = 0), and the only graph that is positive on the same domain is , so 0 = . We conclude that = , = 0, = 00, and = 000. 51. We can immediately see that is the graph of the acceleration function, since at the points where has a horizontal tangent, neither nor is equal to 0. Next, we note that = 0 at the point where has a horizontal tangent, so must be the graph of the velocity function, and hence, 0 = . We conclude that is the graph of the position function. 52. must be the jerk since none of the graphs are 0 at its high and low points. is 0 where has a maximum, so 0 = . is 0 where has a maximum, so 0 = . We conclude that is the position function, is the velocity, is the acceleration, and is the jerk. 53. 0() = lim →0 ( + ) − () = lim →0 [3( + )2 + 2( + ) + 1] − (32 + 2 + 1) = lim →0 (32 + 6 + 32 + 2 + 2 + 1) − (32 + 2 + 1) = lim →0 6 + 32 + 2 = lim →0 (6 + 3 + 2) = lim →0(6 + 3 + 2) = 6 + 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 147 00() = lim →0 0( + ) − 0() = lim →0 [6( + ) + 2] − (6 + 2) = lim →0 (6 + 6 + 2) − (6 + 2) = lim →0 6 = lim →0 6 = 6 We see from the graph that our answers are reasonable because the graph of 0 is that of a linear function and the graph of 00 is that of a constant function. 54. 0() = lim →0 ( + ) − () = lim →0 [( + )3 − 3( + )] − (3 − 3) = lim →0 (3 + 32 + 32 + 3 − 3 − 3) − (3 − 3) = lim →0 32 + 32 + 3 − 3 = lim →0 (32 + 3 + 2 − 3) = lim →0(32 + 3 + 2 − 3) = 32 − 3 00() = lim →0 0( + ) − 0() = lim →0 [3( + )2 −3] − (32 − 3) = lim →0 (32 + 6 + 32− 3) − (32 − 3) = lim →0 6 + 32 = lim →0 (6+ 3) = lim →0(6 + 3) = 6 We see from the graph that our answers are reasonable because the graph of 0 is that of an even function ( is an odd function) and the graph of 00 is that of an odd function. Furthermore, 0 = 0 when has a horizontal tangent and 00 = 0 when 0 has a horizontal tangent. 55. 0() = lim →0 ( + ) − () = lim →0 2( + )2 − ( + )3 − (22 − 3) = lim →0 (4 + 2 − 32 − 3 − 2) = lim →0 (4 + 2 − 32 − 3 − 2) = 4 − 32 00() = lim →0 0( + ) − 0() = lim →0 4( + ) − 3( + )2 − (4 − 32) = lim →0 (4 − 6 − 3) = lim →0 (4 − 6 − 3) = 4 − 6 000() = lim →0 00( + ) − 00() = lim →0 [4 − 6( + )] − (4 − 6) = lim →0 −6 = lim →0 (−6) = −6 (4)() = lim →0 000( + ) − 000() = lim →0 −6 −(−6) = lim →0 0 = lim →0 (0) = 0 The graphs are consistent with the geometric interpretations of the derivatives because 0 has zeros where has a local minimum and a local maximum, 00 has a zero where 0 has a local maximum, and 000 is a constant function equal to the slope of 00. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.148 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 56. (a) Since we estimate the velocity to be a maximum at = 10, the acceleration is 0 at = 10. (b) Drawing a tangent line at = 10 on the graph of , appears to decrease by 10 fts2 over a period of 20 s. So at = 10 s, the jerk is approximately −1020 = −05 (fts2)s or fts3. 57. (a) Note that we have factored − as the difference of two cubes in the third step. 0() = lim → () − () − = lim → 13 − 13 − = lim → 13 − 13 (13 − 13)(23 + 1313 + 23) = lim → 1 23 + 1313 + 23 = 1 323 or 1 3−23 (b) 0(0) = lim →0 (0 + ) − (0) = lim →0 √3 − 0 = lim →0 213 . This function increases without bound, so the limit does not exist, and therefore 0(0) does not exist. (c) lim →0 | 0()| = lim →0 1 323 = ∞ and is continuous at = 0 (root function), so has a vertical tangent at = 0. 58. (a) 0(0) = lim →0 () − (0) − 0 = lim →0 23 − 0 = lim →0 1 13 , which does not exist. (b) 0() = lim → () − () − = lim → 23 − 23 − = lim → (13 − 13)(13 + 13) (13 − 13)(23 + 1313 + 23) = lim → 13 + 13 23 + 1313 + 23 = 213 323 = 2 313 or 2 3−13 (c) () = 23 is continuous at = 0 and lim →0 |0()| = lim →0 2 3 ||13 = ∞. This shows that has a vertical tangent line at = 0. (d) 59. () = | − 6| = − (−6− 6) if if − − 6 6 ≥ 6 0 = 6 −−6 if if ≥ 6 6 So the right-hand limit is lim →6+ () − (6) − 6 = lim →6+ | − 6| − 0 − 6 = lim →6+ − 6 − 6 = lim →6+ 1 = 1, and the left-hand limit is lim →6− () − (6) − 6 = lim →6− | − 6| − 0 − 6 = lim →6− 6 − − 6 = lim →6− (−1) = −1. Since these limits are not equal, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 2.8 THE DERIVATIVE AS A FUNCTION ¤ 149 0(6) = lim →6 () − (6) − 6 does not exist and is not differentiable at 6. However, a formula for 0 is 0() = 1 −1 if if 66 Another way of writing the formula is 0() = − 6 | − 6|. 60. () = [[]] is not continuous at any integer , so is not differentiable at by the contrapositive of Theorem 4. If is not an integer, then is constant on an open interval containing , so 0() = 0. Thus, 0() = 0, not an integer. 61. (a) () = || = −22 if if ≥ 0 0 (b) Since () = 2 for ≥ 0, we have 0() = 2 for 0. [See Exercise 19(d).] Similarly, since () = −2 for 0, we have 0() = −2 for 0. At = 0, we have 0(0) = lim →0 () − (0) − 0 = lim →0 || = lim →0 || = 0 So is differentiable at 0. Thus, is differentiable for all . (c) From part (b), we have 0() = −22 if if ≥ 0 0 = 2 ||. 62. (a) || = − if if ≥ 0 0 so () = + || = 20 if if ≥ 0 0 . Graph the line = 2 for ≥ 0 and graph = 0 (the x-axis) for 0. (b) is not differentiable at = 0 because the graph has a corner there, but is differentiable at all other values; that is, is differentiable on (−∞ 0) ∪ (0 ∞). (c) () = 2 0 if if ≥ 0 0 ⇒ 0() = 20 if if 0 0 Another way of writing the formula is 0() = 1 + sgn for 6= 0. 63. (a) If is even, then 0(−) = lim →0 (− + ) − (−) = lim →0 [−( − )] − (−) = lim →0 ( − ) − () = − lim →0 ( − −)− () [let ∆ = −] = − lim ∆→0 ( + ∆) − () ∆ = − 0() Therefore, 0 is odd. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.150 ¤ CHAPTER 2 LIMITS AND DERIVATIVES (b) If is odd, then 0(−) = lim →0 (− + ) − (−) = lim →0 [−( − )] − (−) = lim →0 −( − ) + () = lim →0 ( − −)− () [let ∆ = −] = lim ∆→0 ( + ∆) − () ∆ = 0() Therefore, 0 is even. 64. (a) −0 (4) = lim →0− (4 + ) − (4) = lim →0− 5 − (4 + ) − 1 = lim →0− − = −1 and +0 (4) = lim →0+ (4 + ) − (4) = lim →0+ 1 5 − (4 + ) − 1 = lim →0+ 1 − (1 − ) (1 − ) = lim →0+ 1 −1 = 1 (b) (c) () = 0 if ≤ 0 5 − if 0 4 1(5 − ) if ≥ 4 At 4 we have lim →4− () = lim →4− (5 − ) = 1 and lim →4+ () = lim →4+ 1 5 − = 1, so lim →4 () = 1 = (4) and is continuous at 4. Since (5) is not defined, is discontinuous at 5. These expressions show that is continuous on the intervals (−∞ 0), (0 4), (4 5) and (5 ∞). Since lim →0+ () = lim →0+ (5 − ) = 5 6= 0 = lim →0− (), lim →0 () does not exist, so is discontinuous (and therefore not differentiable) at 0. (d) From (a), is not differentiable at 4 since −0 (4) 6= +0 (4), and from (c), is not differentiable at 0 or 5. 65. These graphs are idealizations conveying the spirit of the problem. In reality, changes in speed are not instantaneous, so the graph in (a) would not have corners and the graph in (b) would be continuous. (a) (b) 66. (a) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 REVIEW ¤ 151 (b) The initial temperature of the water is close to room temperature because of the water that was in the pipes. When the water from the hot water tank starts coming out, is large and positive as increases to the temperature of the water in the tank. In the next phase, = 0 as the water comes out at a constant, high temperature. After some time, becomes small and negative as the contents of the hot water tank are exhausted. Finally, when the hot water has run out, is once again 0 as the water maintains its (cold) temperature. (c) 67. In the right triangle in the diagram, let ∆ be the side opposite angle and ∆ the side adjacent to angle . Then the slope of the tangent line is = ∆∆ = tan . Note that 0 2 . We know (see Exercise 19) that the derivative of () = 2 is 0() = 2. So the slope of the tangent to the curve at the point (1 1) is 2. Thus, is the angle between 0 and 2 whose tangent is 2; that is, = tan−1 2 ≈ 63◦. 2 Review 1. False. Limit Law 2 applies only if the individual limits exist (these don’t). 2. False. Limit Law 5 cannot be applied if the limit of the denominator is 0 (it is). 3. True. Limit Law 5 applies. 4. False. 2 − 9 − 3 is not defined when = 3, but + 3 is. 5. True. lim →3 2 − 9 − 3 = lim →3 ( + 3)( − 3) ( − 3) = lim →3( + 3) 6. True. The limit doesn’t exist since ()() doesn’t approach any real number as approaches 5. (The denominator approaches 0 and the numerator doesn’t.) 7. False. Consider lim →5 ( − 5) − 5 or lim →5 sin( − 5) − 5 . The first limit exists and is equal to 5. By Example 2.2.3, we know that the latter limit exists (and it is equal to 1). 8. False. If () = 1, () = −1, and = 0, then lim →0 () does not exist, lim →0 () does not exist, but lim →0 [() + ()] = lim →0 0 = 0 exists. 9. True. Suppose that lim → [() + ()] exists. Now lim → () exists and lim → () does not exist, but lim → () = lim → {[() + ()] − ()} = lim → [() + ()] − lim → () [by Limit Law 2], which exists, and we have a contradiction. Thus, lim → [() + ()] does not exist. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.152 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 10. False. Consider lim →6 [()()] = lim →6 ( − 6) −1 6. It exists (its value is 1) but (6) = 0 and (6) does not exist, so (6)(6) 6= 1. 11. True. A polynomial is continuous everywhere, so lim → () exists and is equal to (). 12. False. Consider lim →0 [() − ()] = lim →0 12 − 14 . This limit is −∞ (not 0), but each of the individual functions approaches ∞. 13. True. See Figure 2.6.8. 14. False. Consider () = sin for ≥ 0. lim →∞ () 6= ±∞ and has no horizontal asymptote. 15. False. Consider () = 1 2( − 1) if if 6= 1 = 1 16. False. The function must be continuous in order to use the Intermediate Value Theorem. For example, let () = 1 −1 if if 0 ≤= 3 3 There is no number ∈ [0 3] with () = 0. 17. True. Use Theorem 2.5.8 with = 2, = 5, and () = 42 − 11. Note that (4) = 3 is not needed. 18. True. Use the Intermediate Value Theorem with = −1, = 1, and = , since 3 4. 19. True, by the definition of a limit with = 1. 20. False. For example, let () = 22 + 1 if if 6= 0 = 0 Then () 1 for all , but lim →0 () = lim →0 2 + 1 = 1. 21. False. See the note after Theorem 2.8.4. 22. True. 0() exists ⇒ is differentiable at ⇒ is continuous at ⇒ lim → () = (). 23. False. 2 2 is the second derivative while 2 is the first derivative squared. For example, if = , then 2 2 = 0, but 2 = 1. 24. True. () = 10 − 102 + 5 is continuous on the interval [0 2], (0) = 5, (1) = −4, and (2) = 989. Since −4 0 5, there is a number in (0 1) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation 10 − 102 + 5 = 0 in the interval (0 1). Similarly, there is a root in (1 2). 25. True. See Exercise 2.5.72(b). 26. False See Exercise 2.5.72(b). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 REVIEW ¤ 153 1. (a) (i) lim →2+ () = 3 (ii) lim →−3+ () = 0 (iii) lim →−3 () does not exist since the left and right limits are not equal. (The left limit is −2.) (iv) lim →4 () = 2 (v) lim →0 () = ∞ (vi) lim →2− () = −∞ (vii) lim →∞ () = 4 (viii) lim →−∞ () = −1 (b) The equations of the horizontal asymptotes are = −1 and = 4. (c) The equations of the vertical asymptotes are = 0 and = 2. (d) is discontinuous at = −3, 0, 2, and 4. The discontinuities are jump, infinite, infinite, and removable, respectively. 2. lim →−∞ () = −2, lim →∞ () = 0, lim →−3 () = ∞, lim →3− () = −∞, lim →3+ () = 2, is continuous from the right at 3 3. Since the exponential function is continuous, lim →1 3− = 1−1 = 0 = 1. 4. Since rational functions are continuous, lim →3 2 − 9 2 + 2 − 3 = 32 − 9 32 + 2(3) − 3 = 0 12 = 0. 5. lim →−3 2 − 9 2 + 2 − 3 = lim →−3 ( ( + 3)( + 3)( − − 3) 1) = lim →−3 − − 3 1 = −−33 −− 31 = −−64 = 32 6. lim →1+ 2 − 9 2 + 2 − 3 = −∞ since 2 + 2 − 3 → 0+ as → 1+ and 2 + 2 2 −9− 3 0 for 1 3. 7. lim →0 ( − 1)3 + 1 = lim →0 3 − 32 + 3 − 1 + 1 = lim →0 3 − 32 + 3 = lim →0 2 − 3 + 3 = 3 Another solution: Factor the numerator as a sum of two cubes and then simplify. lim →0 ( − 1)3 + 1 = lim →0 ( − 1) 3 + 13 = lim →0 [( − 1) + 1] ( − 1) 2 − 1( − 1) + 12 = lim →0 ( − 1)2 − + 2 = 1 − 0 + 2 = 3 8. lim →2 2 − 4 3 − 8 = lim →2 ( −(2)( + 2)( 2 + 2 −2) + 4) = lim →2 2 + 2 + 2 + 4 = 4 + 4 + 4 2 + 2 = 12 4 = 1 3 9. lim →9 √ ( − 9)4 = ∞ since ( − 9)4 → 0+ as → 9 and ( √−9)4 0 for 6= 9. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.154 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 10. lim →4+ 4 − |4 − | = lim →4+ −4 (4−−) = lim →4+ −11 = −1 11. lim →1 4 − 1 3 + 52 − 6 = lim →1 ((2+ 1)( 2 + 52−−6) 1) = lim →1 (2+ 1)( ( + 6)( + 1)( −1) − 1) = lim →1 (2+ 1)( ( + 6) + 1) = 2(2) 1(7) = 47 12. lim →3 √ + 6 − 3 − 32 = lim →3 √2(+ 6 −−3) · √√ + 6 + + 6 + = lim →3 2((√−3) + 6 ) √2+ 6 + − 2 = lim →3 + 6 − 2 2( − 3) √ + 6 + = lim →3 2(−−(3)2−√−+ 6 + 6) = lim →3 2(−−(3) −3)( √+ 6 + + 2) = lim →3 −( + 2) 2√ + 6 + = − 5 9(3 + 3) = − 5 54 13. Since is positive, √2 = || = . Thus, lim →∞ √2 − 9 2 − 6 = lim →∞ √2 − 9√2 (2 − 6) = lim →∞ 1 − 92 2 − 6 = √1 − 0 2 − 0 = 1 2 14. Since is negative, √2 = || = −. Thus, lim →−∞ √2 − 9 2 − 6 = lim →−∞ √2 − 9√2 (2 − 6)(−) = lim →−∞ 1 − 92 −2 + 6 = √1 − 0 −2 + 0 = − 1 2 15. Let = sin . Then as → −, sin → 0+, so → 0+. Thus, lim →− ln(sin ) = lim →0+ ln = −∞. 16. lim →−∞ 1 − 22 − 4 5 + − 34 = lim →−∞ (1 (5 + − 2−2 −344)) 44 = lim →−∞ 1 5 4 4 − + 1 2 2 3 − − 1 3 = 00 + 0 − 0 −− 13 = −−13 = 13 17. lim →∞ √2 + 4 + 1 − = lim →∞√2 + 41 + 1 − · √√ 2 2 + 4 + 4 + 1 + + 1 + = lim →∞ (√22+ 4 + 4 + 1) + 1 + − 2 = lim →∞ (4 + 1) ( √2 + 4 + 1 + ) divide by = √2 for 0 = lim →∞ 4 + 1 1 + 4 + 12 + 1 = 4 + 0 √1 + 0 + 0 + 1 = 4 2 = 2 18. Let = − 2 = (1 − ). Then as → ∞, → −∞, and lim →∞ −2 = lim →−∞ = 0. 19. Let = 1. Then as → 0+, → ∞, and lim →0+ tan−1(1) = lim →∞ tan−1 = 2 . 20. lim →1 −1 1 + 2 − 31 + 2 = lim →1 −1 1 + ( − 1)( 1 − 2) = lim →1 ( −1)( −2− 2) + ( − 1)( 1 − 2) = lim →1 ( −1)( −1− 2) = lim →1 −1 2 = 1 −1 2 = −1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 REVIEW ¤ 155 21. From the graph of = cos2 2, it appears that = 0 is the horizontal asymptote and = 0 is the vertical asymptote. Now 0 ≤ (cos )2 ≤ 1 ⇒ 0 2 ≤ cos2 2 ≤ 12 ⇒ 0 ≤ cos 22 ≤ 12 . But →lim±∞0 = 0 and lim →±∞ 1 2 = 0, so by the Squeeze Theorem, lim →±∞ cos2 2 = 0. Thus, = 0 is the horizontal asymptote. lim →0 cos2 2 = ∞ because cos2 → 1 and 2 → 0+ as → 0, so = 0 is the vertical asymptote. 22. From the graph of = () = √2 + + 1 − √2 − , it appears that there are 2 horizontal asymptotes and possibly 2 vertical asymptotes. To obtain a different form for , let’s multiply and divide it by its conjugate. 1() = √2 + + 1 − √2 − √2 + + 1 + √2 − √2 + + 1 + √2 − = (2 + + 1) − (2 − ) √2 + + 1 + √2 − = 2 + 1 √2 + + 1 + √2 − Now lim →∞ 1() = lim →∞ 2 + 1 √2 + + 1 + √2 − = lim →∞ 2 + (1) 1 + (1) + (12) + 1 − (1) [since √2 = for 0] = 2 1 + 1 = 1, so = 1 is a horizontal asymptote. For 0, we have √2 = || = −, so when we divide the denominator by , with 0, we get √2 + + 1 + √2 − = − √2 + + 1 + √2 − √2 = − 1 + 1 + 12 + 1 − 1 Therefore, lim →−∞ 1() = lim →−∞ 2 + 1 √2 + + 1 + √2 − = lim →∞ − 1 + (1) + (1 2 + (1 2) + ) 1 − (1) = 2 −(1 + 1) = −1 so = −1 is a horizontal asymptote. The domain of is (−∞ 0] ∪ [1 ∞). As → 0−, () → 1, so = 0 is not a vertical asymptote. As → 1+, () → √3, so = 1 is not a vertical asymptote and hence there are no vertical asymptotes. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.156 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 23. Since 2 − 1 ≤ () ≤ 2 for 0 3 and lim →1 (2 − 1) = 1 = lim →1 2, we have lim →1 () = 1 by the Squeeze Theorem. 24. Let () = −2, () = 2 cos12 and () = 2. Then since cos12 ≤ 1 for 6= 0, we have () ≤ () ≤ () for 6= 0, and so lim →0 () = lim →0 () = 0 ⇒ lim →0 () = 0 by the Squeeze Theorem. 25. Given 0, we need 0 such that if 0 | − 2| , then |(14 − 5) − 4| . But |(14 − 5) − 4| ⇔ |−5 + 10| ⇔ |−5| | − 2| ⇔ | − 2| 5. So if we choose = 5, then 0 | − 2| ⇒ |(14 − 5) − 4| . Thus, lim →2 (14 − 5) = 4 by the definition of a limit. 26. Given 0 we must find 0 so that if 0 | − 0| , then |√3 − 0| . Now |√3 − 0| = |√3 | ⇒ || = |√3 |3 3. So take = 3. Then 0 | − 0| = || 3 ⇒ |√3 − 0| = |√3 | = 3 || √3 3 = . Therefore, by the definition of a limit, lim →0 √3 = 0. 27. Given 0, we need 0 so that if 0 | − 2| , then 2 − 3 − (−2) . First, note that if | − 2| 1, then −1 − 2 1, so 0 − 1 2 ⇒ | − 1| 2. Now let = min {2 1}. Then 0 | − 2| ⇒ 2 − 3 − (−2) = |( − 2)( − 1)| = | − 2| | − 1| (2)(2) = . Thus, lim →2 (2 − 3) = −2 by the definition of a limit. 28. Given 0, we need 0 such that if 0 − 4 , then 2√ − 4 . This is true ⇔ √ − 4 2 ⇔ − 4 4 2. So if we choose = 4 2, then 0 − 4 ⇒ 2√ − 4 . So by the definition of a limit, lim →4+ 2√ − 4 = ∞. 29. (a) () = √− if 0, () = 3 − if 0 ≤ 3, () = ( − 3)2 if 3. (i) lim →0+ () = lim →0+ (3 − ) = 3 (ii) lim →0− () = lim →0− √− = 0 (iii) Because of (i) and (ii), lim →0 () does not exist. (iv) lim →3− () = lim →3− (3 − ) = 0 (v) lim →3+ () = lim →3+ ( − 3)2 = 0 (vi) Because of (iv) and (v), lim →3 () = 0. (b) is discontinuous at 0 since lim →0 () does not exist. is discontinuous at 3 since (3) does not exist. (c) 30. (a) () = 2 − 2 if 0 ≤ ≤ 2, () = 2 − if 2 ≤ 3, () = − 4 if 3 4, () = if ≥ 4. Therefore, lim →2− () = lim →2− 2 − 2 = 0 and lim →2+ () = lim →2+ (2 − ) = 0. Thus, lim →2 () = 0 = (2), so is continuous at 2. lim →3− () = lim →3− (2 − ) = −1 and lim →3+ () = lim →3+ ( − 4) = −1. Thus, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 REVIEW ¤ 157 lim →3 () = −1 = (3), so is continuous at 3. lim →4− () = lim →4− ( − 4) = 0 and lim →4+ () = lim →4+ = . Thus, lim →4 () does not exist, so is discontinuous at 4. But lim →4+ () = = (4), so is continuous from the right at 4. (b) 31. sin and are continuous on R by Theorem 2.5.7. Since is continuous on R, sin is continuous on R by Theorem 2.5.9. Lastly, is continuous on R since it’s a polynomial and the product sin is continuous on its domain R by Theorem 2.5.4. 32. 2 − 9 is continuous on R since it is a polynomial and √ is continuous on [0 ∞) by Theorem 2.5.7, so the composition √2 − 9 is continuous on | 2 − 9 ≥ 0 = (−∞ −3] ∪ [3 ∞) by Theorem 2.5.9. Note that 2 − 2 6= 0 on this set and so the quotient function () = √2 − 9 2 − 2 is continuous on its domain, (−∞ −3] ∪ [3 ∞) by Theorem 2.5.4. 33. () = 5 − 3 + 3 − 5 is continuous on the interval [1 2], (1) = −2, and (2) = 25. Since −2 0 25, there is a number in (1 2) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation 5 − 3 + 3 − 5 = 0 in the interval (1 2). 34. () = cos √ − + 2 is continuous on the interval [0 1], (0) = 2, and (1) ≈ −02. Since −02 0 2, there is a number in (0 1) such that () = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation cos √ − + 2 = 0, or cos √ = − 2, in the interval (0 1). 35. (a) The slope of the tangent line at (2 1) is lim →2 () − (2) − 2 = lim →2 9 − 22 − 1 − 2 = lim →2 8 − 22 − 2 = lim →2 −2(2 − 4) − 2 = lim →2 −2( − 2)( + 2) − 2 = lim →2 [−2( + 2)] = −2 · 4 = −8 (b) An equation of this tangent line is − 1 = −8( − 2) or = −8 + 17. 36. For a general point with -coordinate , we have = lim → 2(1 − 3) − 2(1 − 3) − = lim → 2(1 − 3) − 2(1 − 3) (1 − 3)(1 − 3)( − ) = lim → (1 − 3)(1 6(−−3))( − ) = lim → 6 (1 − 3)(1 − 3) = 6 (1 − 3)2 For = 0, = 6 and (0) = 2, so an equation of the tangent line is − 2 = 6( − 0) or = 6 + 2 For = −1, = 3 8 and (−1) = 1 2, so an equation of the tangent line is − 1 2 = 3 8( + 1) or = 3 8 + 7 8. 37. (a) = () = 1 + 2 + 24. The average velocity over the time interval [1 1 + ] is ave = (1 + ) − (1) (1 + ) − 1 = 1 + 2(1 + ) + (1 + )24 − 134 = 10 + 2 4 = 10 + 4 [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.158 ¤ CHAPTER 2 LIMITS AND DERIVATIVES So for the following intervals the average velocities are: (i) [1 3]: = 2, ave = (10 + 2)4 = 3 ms (ii) [1 2]: = 1, ave = (10 + 1)4 = 275 ms (iii) [1 15]: = 05, ave = (10 + 05)4 = 2625 ms (iv) [1 11]: = 01, ave = (10 + 01)4 = 2525 ms (b) When = 1, the instantaneous velocity is lim →0 (1 + ) − (1) = lim →0 10 + 4 = 10 4 = 25 ms. 38. (a) When increases from 200 in3 to 250 in3, we have ∆ = 250 − 200 = 50 in3, and since = 800 , ∆ = (250) − (200) = 800 250 − 800 200 = 32 − 4 = −08 lbin2. So the average rate of change is ∆ ∆ = −08 50 = −0016 lbin2 in3 . (b) Since = 800 , the instantaneous rate of change of with respect to is lim →0 ∆ ∆ = lim →0 ( + ) − () = lim →0 800( + ) − 800 = lim →0 800 [ (−+()+ )] = lim →0 −800 ( + ) = − 800 2 which is inversely proportional to the square of . 39. (a) 0(2) = lim →2 () − (2) − 2 = lim →2 3 − 2 − 4 − 2 = lim →2 ( − 2)(2 + 2 + 2) − 2 = lim →2 (2 + 2 + 2) = 10 (c) (b) − 4 = 10( − 2) or = 10 − 16 40. 26 = 64, so () = 6 and = 2. 41. (a) 0() is the rate at which the total cost changes with respect to the interest rate. Its units are dollars(percent per year). (b) The total cost of paying off the loan is increasing by $1200(percent per year) as the interest rate reaches 10%. So if the interest rate goes up from 10% to 11%, the cost goes up approximately $1200. (c) As increases, increases. So 0() will always be positive. 42. 43. 44. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 REVIEW ¤ 159 45. (a) 0() = lim →0 ( + ) − () = lim →0 3 − 5( + ) − √3 − 5 3 − 5( + ) + √3 − 5 3 − 5( + ) + √3 − 5 = lim →0 [3 − 5( + )] − (3 − 5) 3 − 5( + ) + √3 − 5 = lim →0 3 − 5( +−5) + √3 − 5 = 2√3−−5 5 (b) Domain of : (the radicand must be nonnegative) 3 − 5 ≥ 0 ⇒ 5 ≤ 3 ⇒ ∈ −∞ 3 5 Domain of 0: exclude 3 5 because it makes the denominator zero; ∈ −∞ 3 5 (c) Our answer to part (a) is reasonable because 0() is always negative and is always decreasing. 46. (a) As → ±∞, () = (4 − )(3 + ) → −1, so there is a horizontal asymptote at = −1. As → −3+, () → ∞, and as → −3−, () → −∞. Thus, there is a vertical asymptote at = −3. (b) Note that is decreasing on (−∞ −3) and (−3 ∞), so 0 is negative on those intervals. As → ±∞, 0 → 0. As → −3− and as → −3+, 0 → −∞. (c) 0() = lim →0 ( + ) − () = lim →0 4 − ( + ) 3 + ( + ) − 4 − 3 + = lim →0 (3 + ) [4 −([3 + ( + )]+−(4 )] (3 + − ) [3 + ( ) + )] = lim →0 (12 − 3 − 3 + 4 − 2 − ) − (12 + 4 + 4 − 3 − 2 − ) [3 + ( + )](3 + ) = lim →0 −7 [3 + ( + )] (3 + ) = lim →0 [3 + ( +−7)] (3 + ) = −(3 +7)2 (d) The graphing device confirms our graph in part (b). 47. is not differentiable: at = −4 because is not continuous, at = −1 because has a corner, at = 2 because is not continuous, and at = 5 because has a vertical tangent. 48. The graph of has tangent lines with positive slope for 0 and negative slope for 0, and the values of fit this pattern, so must be the graph of the derivative of the function for . The graph of has horizontal tangent lines to the left and right of the -axis and has zeros at these points. Hence, is the graph of the derivative of the function for . Therefore, is the graph of , is the graph of 0, and is the graph of 00. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.160 ¤ CHAPTER 2 LIMITS AND DERIVATIVES 49. Domain: (−∞ 0) ∪ (0 ∞); lim →0− () = 1; lim →0+ () = 0; 0() 0 for all in the domain; lim →−∞ 0() = 0; lim →∞ 0() = 1 50. (a) 0() is the rate at which the percentage of Americans under the age of 18 is changing with respect to time. Its units are percent per year (%yr). (b) To find 0(), we use lim →0 ( + ) − () ≈ ( + ) − () for small values of . For 1950: 0(1950) ≈ (1960) − (1950) 1960 − 1950 = 357 − 311 10 = 046 For 1960: We estimate 0(1960) by using = −10 and = 10, and then average the two results to obtain a final estimate. = −10 ⇒ 0(1960) ≈ (1950) − (1960) 1950 − 1960 = 311 − 357 −10 = 046 = 10 ⇒ 0(1960) ≈ (1970) − (1960) 1970 − 1960 = 340 − 357 10 = −017 So we estimate that 0(1960) ≈ 1 2[046 + (−017)] = 0145. 1950 1960 1970 1980 1990 2000 2010 0() 0460 0145 −0385 −0415 −0115 −0085 −0170 (c) (d) We could get more accurate values for 0() by obtaining data for the mid-decade years 1955, 1965, 1975, 1985, 1995, and 2005. 51. 0() is the rate at which the number of US $20 bills in circulation is changing with respect to time. Its units are billions of bills per year. We use a symmetric difference quotient to estimate 0(2000). 0(2000) ≈ (2005) − (1995) 2005 − 1995 = 577 − 421 10 = 0156 billions of bills per year (or 156 million bills per year). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 REVIEW ¤ 161 52. (a) Drawing slope triangles, we obtain the following estimates: 0(1950) ≈ 110 1 = 011, 0(1965) ≈ −10 16 = −016, and 0(1987) ≈ 010 2 = 002. (b) The rate of change of the average number of children born to each woman was increasing by 011 in 1950, decreasing by 016 in 1965, and increasing by 002 in 1987. (c) There are many possible reasons: • In the baby-boom era (post-WWII), there was optimism about the economy and family size was rising. • In the baby-bust era, there was less economic optimism, and it was considered less socially responsible to have a large family. • In the baby-boomlet era, there was increased economic optimism and a return to more conservative attitudes. 53. |()| ≤ () ⇔ −() ≤ () ≤ () and lim → () = 0 = lim → −(). Thus, by the Squeeze Theorem, lim → () = 0. 54. (a) Note that is an even function since () = (−). Now for any integer , [[]] + [[−]] = − = 0, and for any real number which is not an integer, [[]] + [[−]] = [[]] + (− [[]] − 1) = −1. So lim → () exists (and is equal to −1) for all values of . (b) is discontinuous at all integers. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.162 ¤ CHAPTER 2 LIMITS AND DERIVATIVES °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.PROBLEMS PLUS 1. Let = √6 , so = 6. Then → 1 as → 1, so lim →1 √3 − 1 √ − 1 = lim →1 2 3 − − 1 1 = lim →1 ( −(1) ( − 1)( 2 ++ 1) + 1) = lim →1 2 ++ 1 + 1 = 12 1 + 1 + 1 + 1 = 23. Another method: Multiply both the numerator and the denominator by (√ + 1)√3 2 + √3 + 1. 2. First rationalize the numerator: lim →0 √ + − 2 · √ + + 2 √ + + 2 = lim →0 √++ − + 2 4 . Now since the denominator approaches 0 as → 0, the limit will exist only if the numerator also approaches 0 as → 0. So we require that (0) + − 4 = 0 ⇒ = 4. So the equation becomes lim →0 √ + 4 + 2 = 1 ⇒ √4 + 2 = 1 ⇒ = 4. Therefore, = = 4. 3. For − 1 2 1 2, we have 2 − 1 0 and 2 + 1 0, so |2 − 1| = −(2 − 1) and |2 + 1| = 2 + 1. Therefore, lim →0 |2 − 1| − |2 + 1| = lim →0 −(2 − 1) − (2 + 1) = lim →0 −4 = lim →0 (−4) = −4. 4. Let be the midpoint of , so the coordinates of are 1 2 1 22 since the coordinates of are 2. Let = (0 ). Since the slope = 2 = , = − 1 (negative reciprocal). But = 12 2 − 12 − 0 = 2 − 2 , so we conclude that −1 = 2 − 2 ⇒ 2 = 2 + 1 ⇒ = 1 22 + 1 2. As → 0, → 1 2 and the limiting position of is 0 1 2. 5. (a) For 0 1, [[]] = 0, so [[]] = 0, and lim →0+ [[]] = 0. For −1 0, [[]] = −1, so [[]] = −1 , and lim →0− [[]] = lim →0− −1 = ∞. Since the one-sided limits are not equal, lim →0 [[ ]] does not exist. (b) For 0, 1 − 1 ≤ [[1]] ≤ 1 ⇒ (1 − 1) ≤ [[1]] ≤ (1) ⇒ 1 − ≤ [[1]] ≤ 1. As → 0+, 1 − → 1, so by the Squeeze Theorem, lim →0+ [[1]] = 1. For 0, 1 − 1 ≤ [[1]] ≤ 1 ⇒ (1 − 1) ≥ [[1]] ≥ (1) ⇒ 1 − ≥ [[1]] ≥ 1. As → 0−, 1 − → 1, so by the Squeeze Theorem, lim →0− [[1]] = 1. Since the one-sided limits are equal, lim →0 [[1]] = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 163 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.164 ¤ CHAPTER 2 PROBLEMS PLUS 6. (a) [[]]2 + [[]]2 = 1. Since [[]]2 and [[]]2 are positive integers or 0, there are only 4 cases: Case (i): [[]] = 1, [[]] = 0 ⇒1 ≤ 2 and 0 ≤ 1 Case (ii): [[]] = −1, [[]] = 0 ⇒−1 ≤ 0 and 0 ≤ 1 Case (iii):[[]] = 0, [[]] = 1 ⇒0 ≤ 1 and 1 ≤ 2 Case (iv):[[]] = 0, [[]] = −1 ⇒0 ≤ 1 and −1 ≤ 0 (b) [[]]2 − [[]]2 = 3. The only integral solution of 2 − 2 = 3 is = ±2 and = ±1. So the graph is {( ) | [[]] = ±2, [[]] = ±1} = ( ) 21 ≤≤ ≤ 23 or or −−12 ≤≤ 01 . (c) [[ + ]]2 = 1 ⇒ [[ + ]] = ±1 ⇒ 1 ≤ + 2 or −1 ≤ + 0 (d) For ≤ + 1, [[]] = . Then [[]] + [[]] = 1 ⇒ [[]] = 1 − ⇒ 1 − ≤ 2 − . Choosing integer values for produces the graph. 7. is continuous on (−∞ ) and ( ∞). To make continuous on R, we must have continuity at . Thus, lim →+ () = lim →− () ⇒ lim →+ 2 = lim →− ( + 1) ⇒ 2 = + 1 ⇒ 2 − − 1 = 0 ⇒ [by the quadratic formula] = 1 ± √5 2 ≈ 1618 or −0618. 8. (a) Here are a few possibilities: (b) The “obstacle” is the line = (see diagram). Any intersection of the graph of with the line = constitutes a fixed point, and if the graph of the function does not cross the line somewhere in (0 1), then it must either start at (0 0) (in which case 0 is a fixed point) or finish at (1 1) (in which case 1 is a fixed point). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 2 PROBLEMS PLUS ¤ 165 (c) Consider the function () = () − , where is any continuous function with domain [0 1] and range in [0 1]. We shall prove that has a fixed point. Now if (0) = 0 then we are done: has a fixed point (the number 0), which is what we are trying to prove. So assume (0) 6= 0. For the same reason we can assume that (1) 6= 1. Then (0) = (0) 0 and (1) = (1) − 1 0. So by the Intermediate Value Theorem, there exists some number in the interval (0 1) such that () = () − = 0. So () = , and therefore has a fixed point. 9. lim → [() + ()] = 2 lim → [() − ()] = 1 ⇒ lim → () + lim → () = 2 (1) lim → () − lim → () = 1 (2) Adding equations (1) and (2) gives us 2 lim → () = 3 ⇒ lim → () = 3 2. From equation (1), lim → () = 1 2. Thus, lim → [() ()] = lim → () · lim → () = 3 2 · 1 2 = 3 4. 10. (a) Solution 1: We introduce a coordinate system and drop a perpendicular from , as shown. We see from ∠ that tan 2 = 1 − , and from ∠ that tan = . Using the double-angle formula for tangents, we get 1 − = tan 2 = 2 tan 1 − tan2 = 2( ) 1 − ( )2 . After a bit of simplification, this becomes 1 1 − = 2 2 − 2 ⇔ 2 = (3 − 2). As the altitude decreases in length, the point will approach the -axis, that is, → 0, so the limiting location of must be one of the roots of the equation (3 − 2) = 0. Obviously it is not = 0 (the point can never be to the left of the altitude , which it would have to be in order to approach 0) so it must be 3 − 2 = 0, that is, = 2 3. Solution 2: We add a few lines to the original diagram, as shown. Now note that ∠ = ∠ (alternate angles; k by symmetry) and similarly ∠ = ∠. So ∆ and ∆ are isosceles, and the line segments , and are all of equal length. As || → 0, and approach points on the base, and the point is seen to approach a position two-thirds of the way between and , as above. (b) The equation 2 = (3 − 2) calculated in part (a) is the equation of the curve traced out by . Now as || → ∞, 2 → 2 , → 4 , → 1, and since tan = , → 1. Thus, only traces out the part of the curve with 0 ≤ 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.166 ¤ CHAPTER 2 PROBLEMS PLUS 11. (a) Consider () = ( + 180◦) − (). Fix any number . If () = 0, we are done: Temperature at = Temperature at + 180◦. If () 0, then ( + 180◦) = ( + 360◦) − ( + 180◦) = () − ( + 180◦) = −() 0. Also, is continuous since temperature varies continuously. So, by the Intermediate Value Theorem, has a zero on the interval [ + 180◦]. If () 0, then a similar argument applies. (b) Yes. The same argument applies. (c) The same argument applies for quantities that vary continuously, such as barometric pressure. But one could argue that altitude above sea level is sometimes discontinuous, so the result might not always hold for that quantity. 12. 0() = lim →0 ( + ) − () = lim →0 ( + )( + ) − () = lim →0 ( + ) − () + (+ ) = lim →0 ( + ) − () + lim →0 ( + ) = 0() + () because is differentiable and therefore continuous. 13. (a) Put = 0 and = 0 in the equation: (0 + 0) = (0) + (0) + 02 · 0 + 0 · 02 ⇒ (0) = 2(0). Subtracting (0) from each side of this equation gives (0) = 0. (b) 0(0) = lim →0 (0 + ) − (0) = lim →0 (0) + () + 02 + 02 − (0) = lim →0 () = lim →0 () = 1 (c) 0() = lim →0 ( + ) − () = lim →0 () + () + 2 + 2 − () = lim →0 () + 2 + 2 = lim →0 () + 2 + = 1 + 2 14. We are given that |()| ≤ 2 for all . In particular, |(0)| ≤ 0, but || ≥ 0 for all . The only conclusion is that (0) = 0. Now () − (0) − 0 = () = |()| || ≤ |2| = |2| = || ⇒ −|| ≤ () −− 0(0) ≤ ||. But lim →0 (−||) = 0 = lim →0 ||, so by the Squeeze Theorem, lim →0 () − (0) − 0 = 0. So by the definition of a derivative, is differentiable at 0 and, furthermore, 0(0) = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved. [Show More]
Last updated: 3 years ago
Preview 1 out of 1 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$10.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Jan 06, 2020
Number of pages
1
Written in
All
Additional information
This document has been written for:
Uploaded
Jan 06, 2020
Downloads
0
Views
350






.png)
.png)
.png)
.png)
.png)
.png)
.png)