Physics 223 Name:
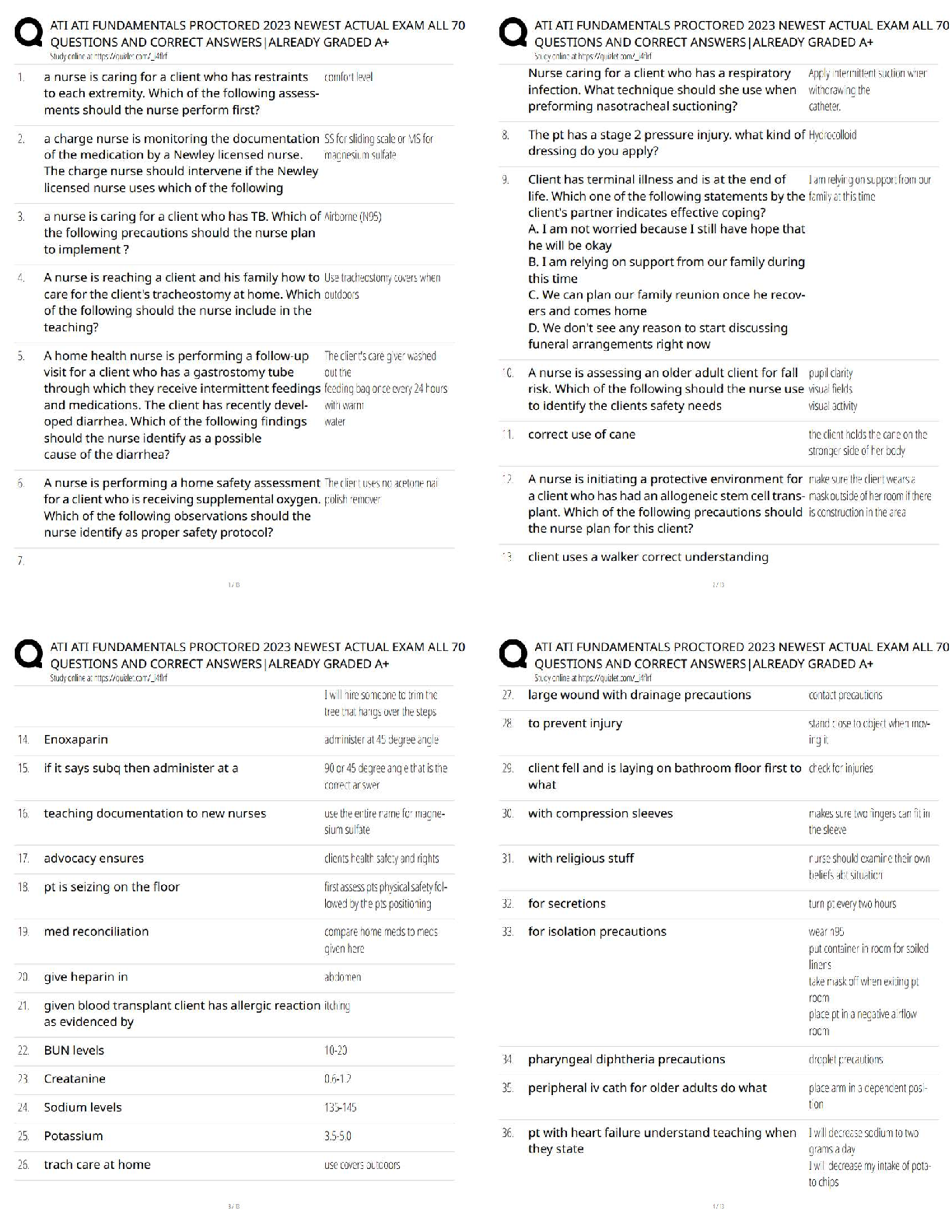
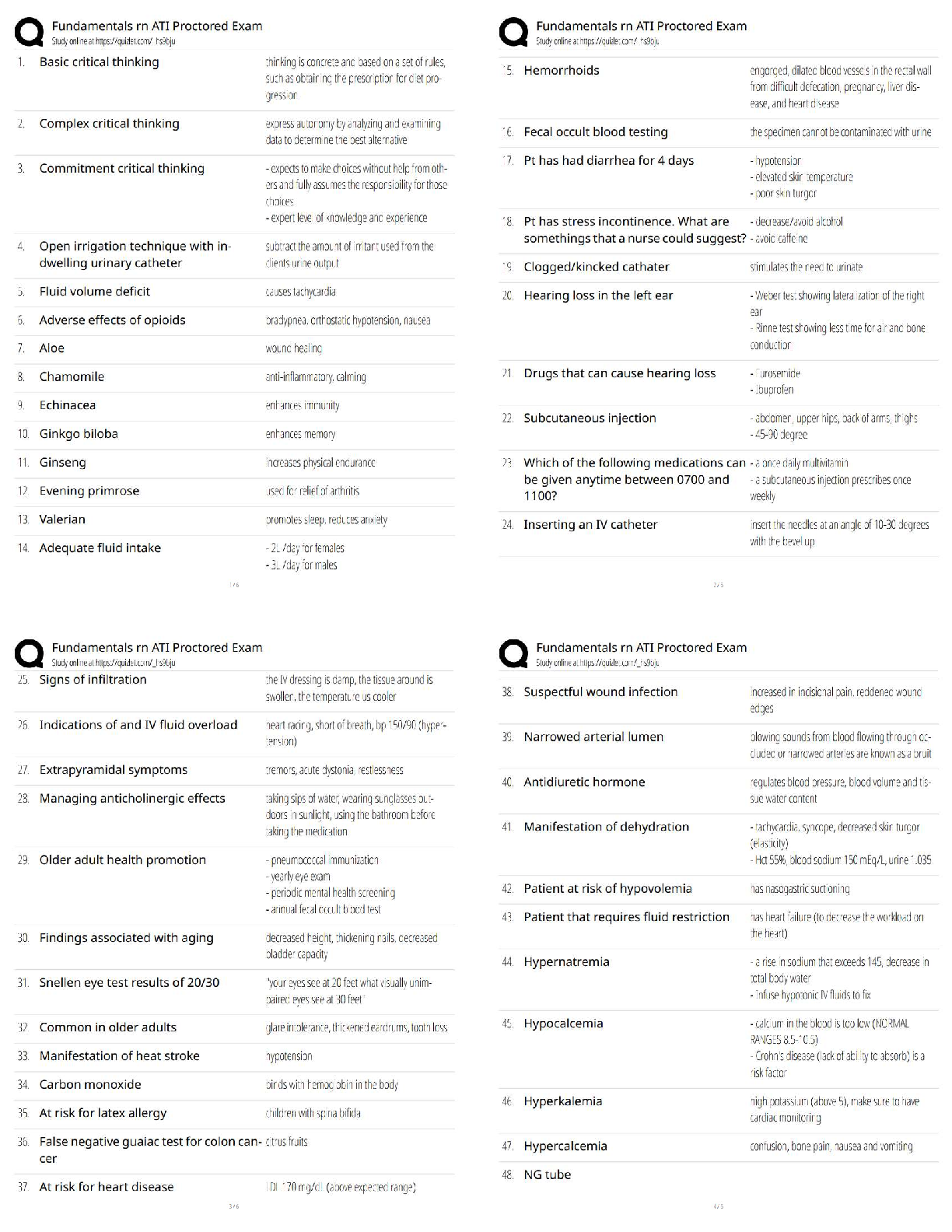
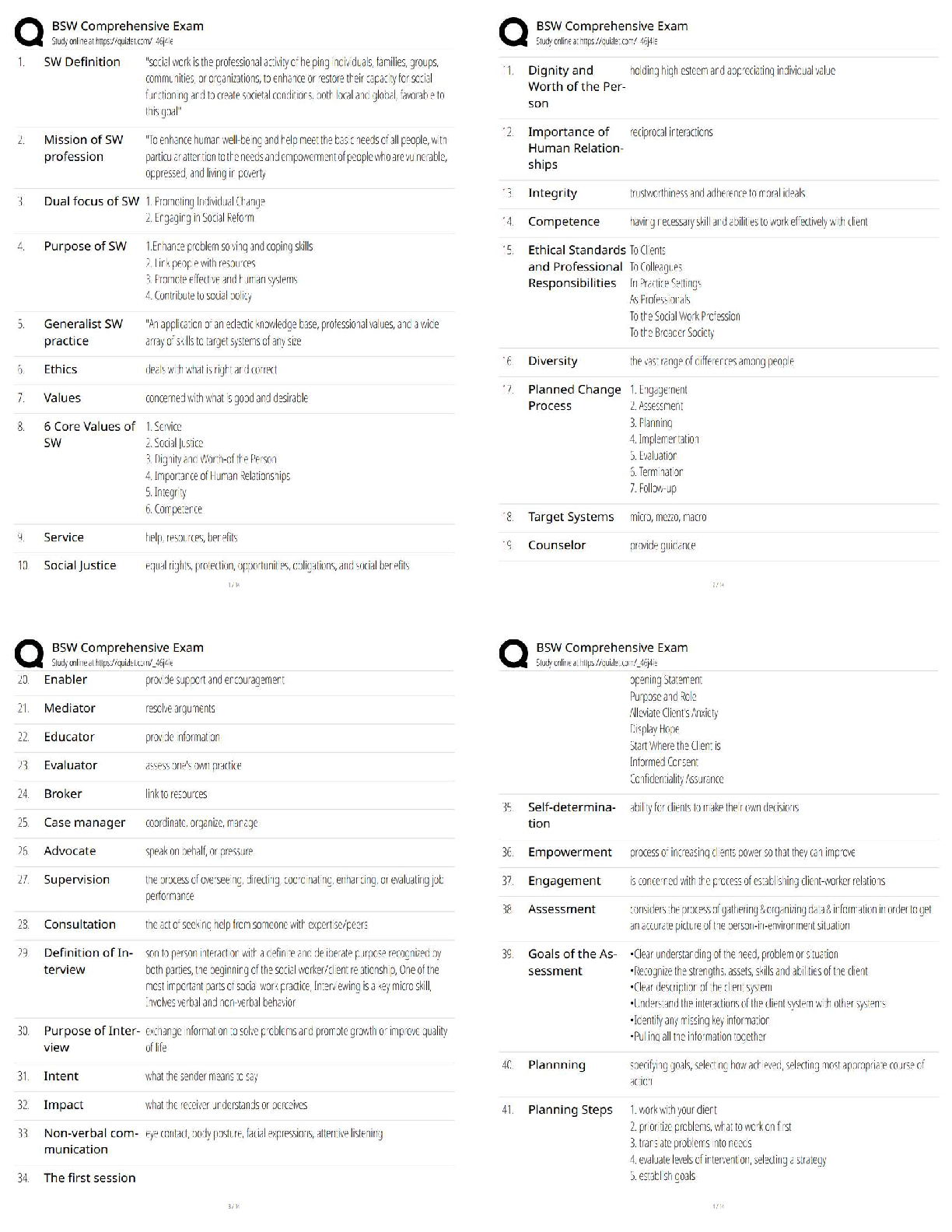
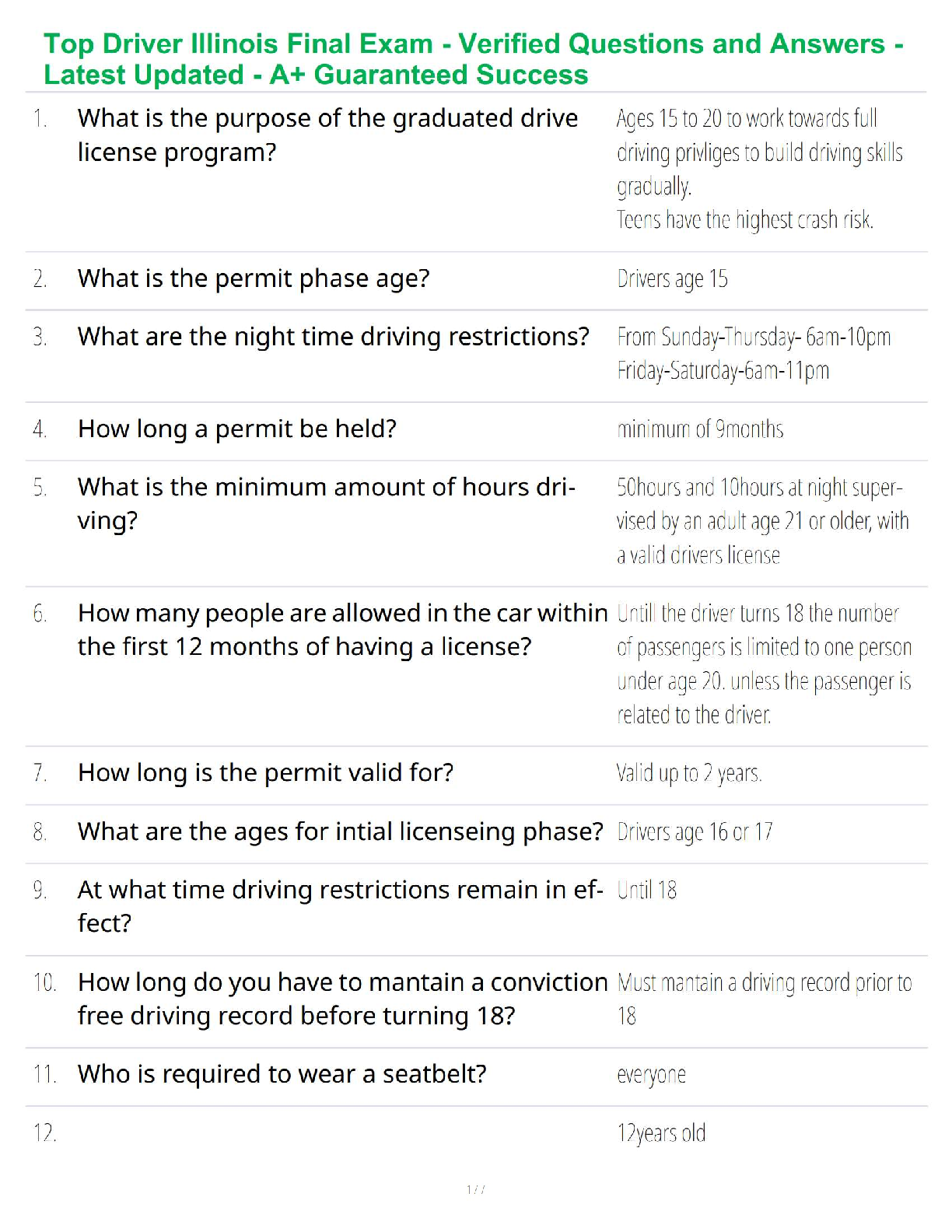
Task 1: Simple Harmonic Motion
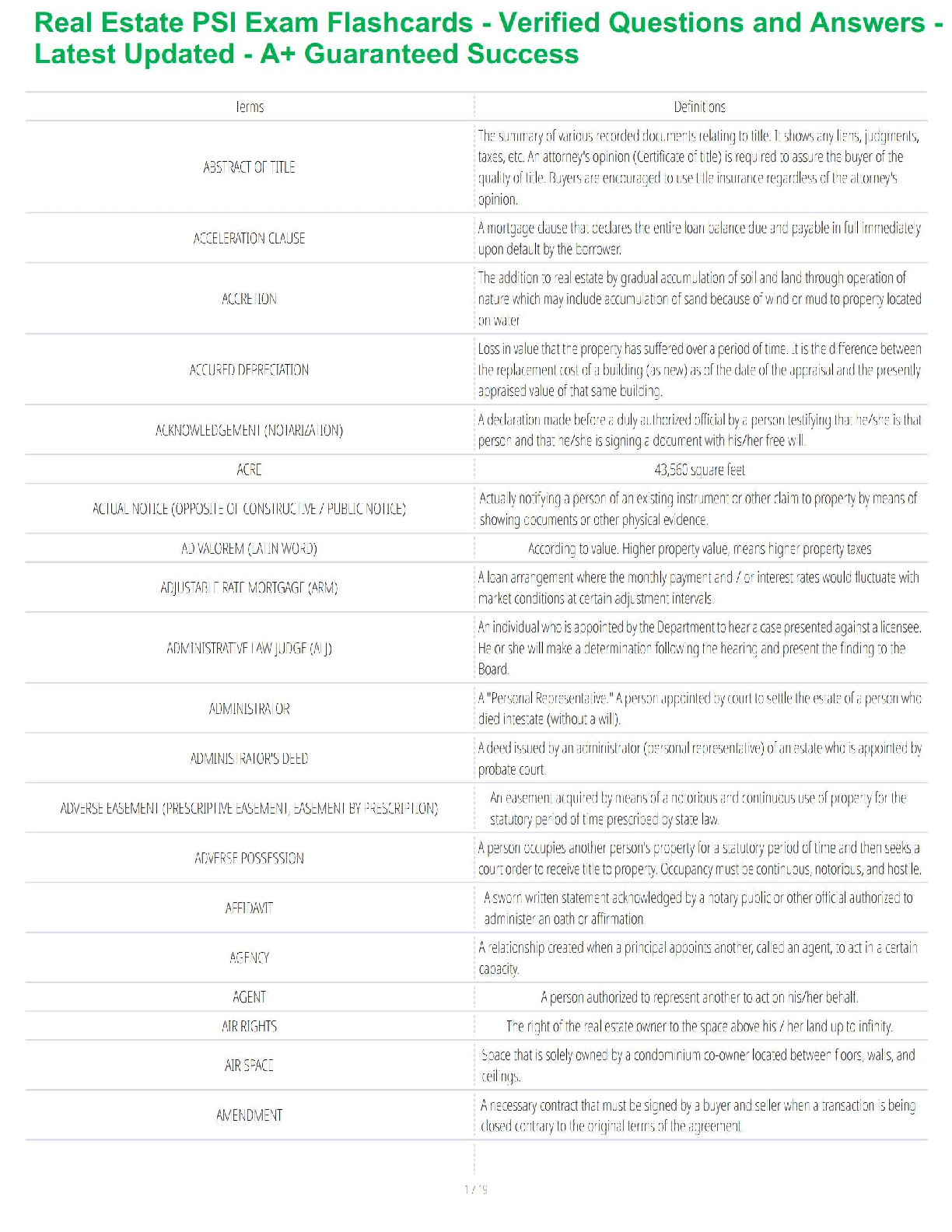
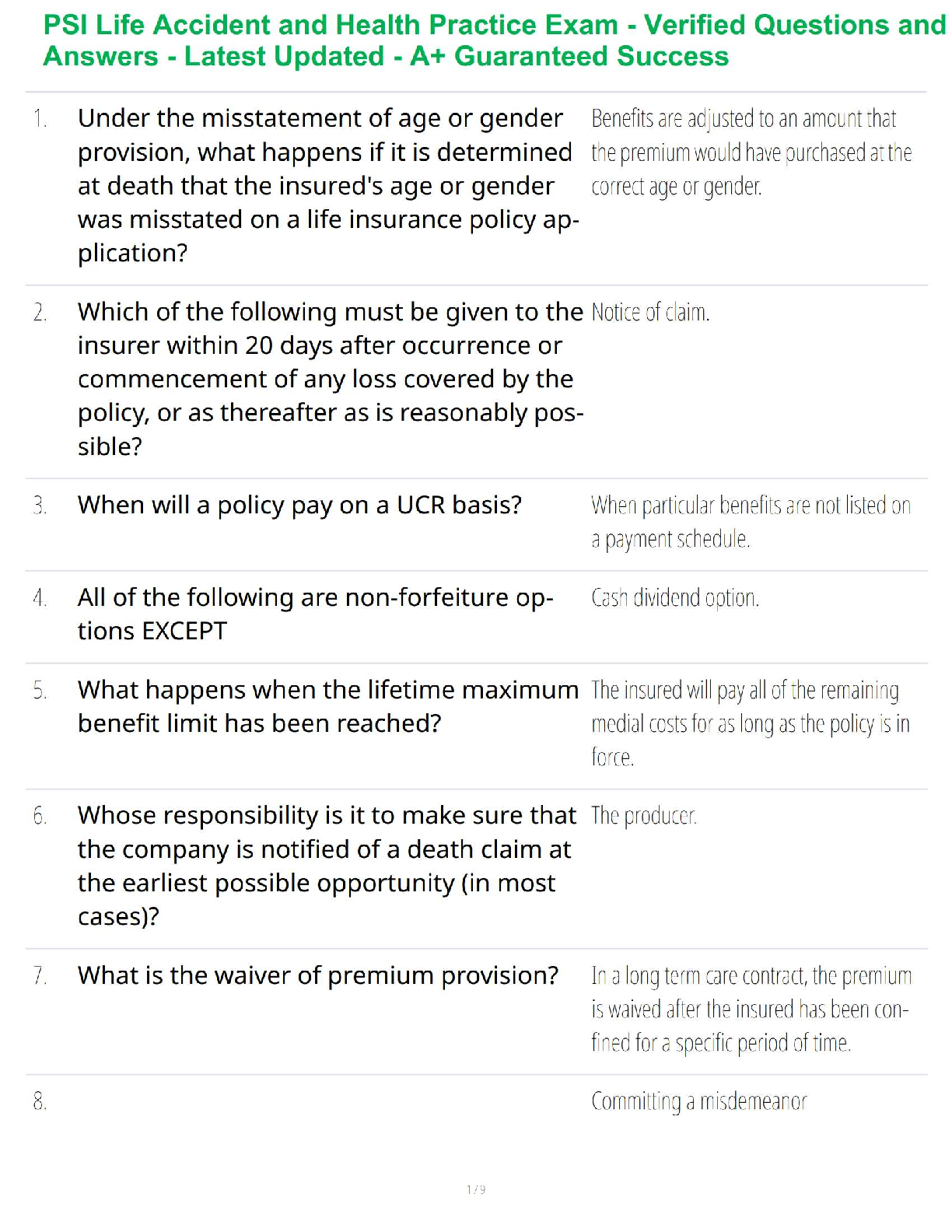
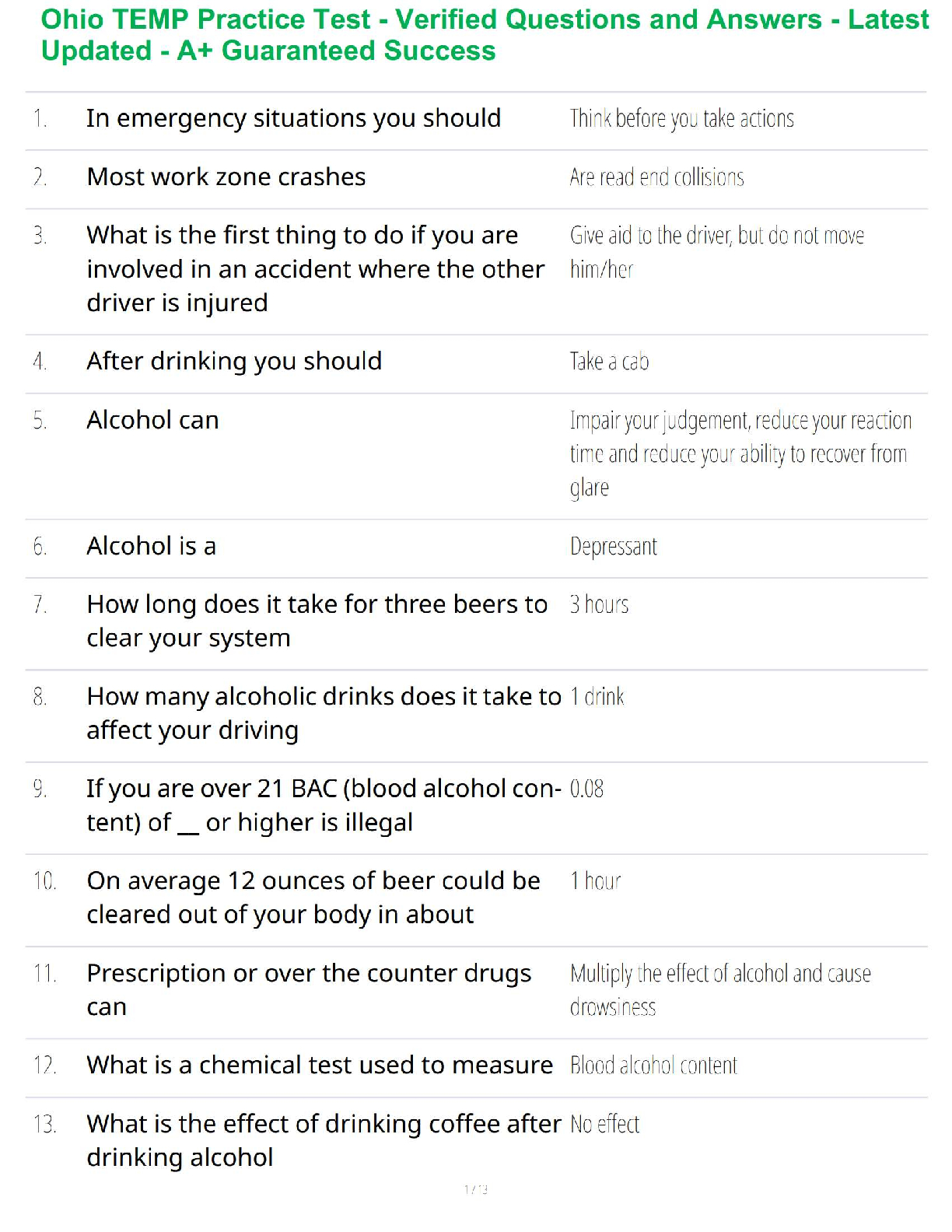
Simple harmonic motion (SHM) is the description of rhythmic cyclical motion,
such as exhibited by a pendulum or a weight on a stretched spring. For such
motion, the am
...
Physics 223 Name:
Task 1: Simple Harmonic Motion
Simple harmonic motion (SHM) is the description of rhythmic cyclical motion,
such as exhibited by a pendulum or a weight on a stretched spring. For such
motion, the amount of distance away from the "middle point" of the motion (for
instance, the weight hanging straight down from a spring that will be stretched)
is called the displacement, and it is given by the scalar equation:
where y is the displacement, A is the amplitude (a constant), ù is the angular
frequency (another constant), t is the time after motion begins (assume motion
begins at t = 0) and ö is the phase angle (still another constant, measured in
radians). Note that this equation can be considered a vector equation, if the sign
of y is used.
a. Use a piece of engineering graph paper to plot the time versus the
displacement for one complete oscillation, which means from the time when the
motion begins to the time when the motion brings the object back to the same
displacement it had when it started. A, ù and ö are arbitrary constants (in other
words, no actual numbers). Be careful in putting the independent variable along
the x-axis, and how you label the axes of your graph.
b. Find and express in terms of y. Recall that means !!!!!!. Don't forget about
the chain rule.
c. The period T is the time required to complete one oscillation. Find T of an
object which obeys the following equation of motion:
y = 0.60 cos (15t – ð/2)
where y is measured in centimeters and t is measured in seconds.
d. The phase angle is often not included in the displacement equation because it
can be “folded” into a sine or cosine term. Using trigonometric identities, recast
the equation for y in part c such that the right side of the equation does not
contain the ð/2, or any radian-based constants at all. Note that the graph of the
function should remain the same!
e. Show that ! = !!!!(!"!!) + !!!!!(!"!!) (or, if you prefer, y = C1 exp[i(ùt + ö)] +
C2 exp[–i(ùt + ö)]) is a solution for the differential equation in part b. Again, be
careful about the chain rule. Note: the “i” refers to – 1 ; that is, !! = -1.
f. Using the complex plane construction, show that ! = !!!!(!"!!) +
!!!!!(!"!!)is equivalent to y = A cos (ùt + ö) for a judicious choice of C1, C2 and A.
[Show More]