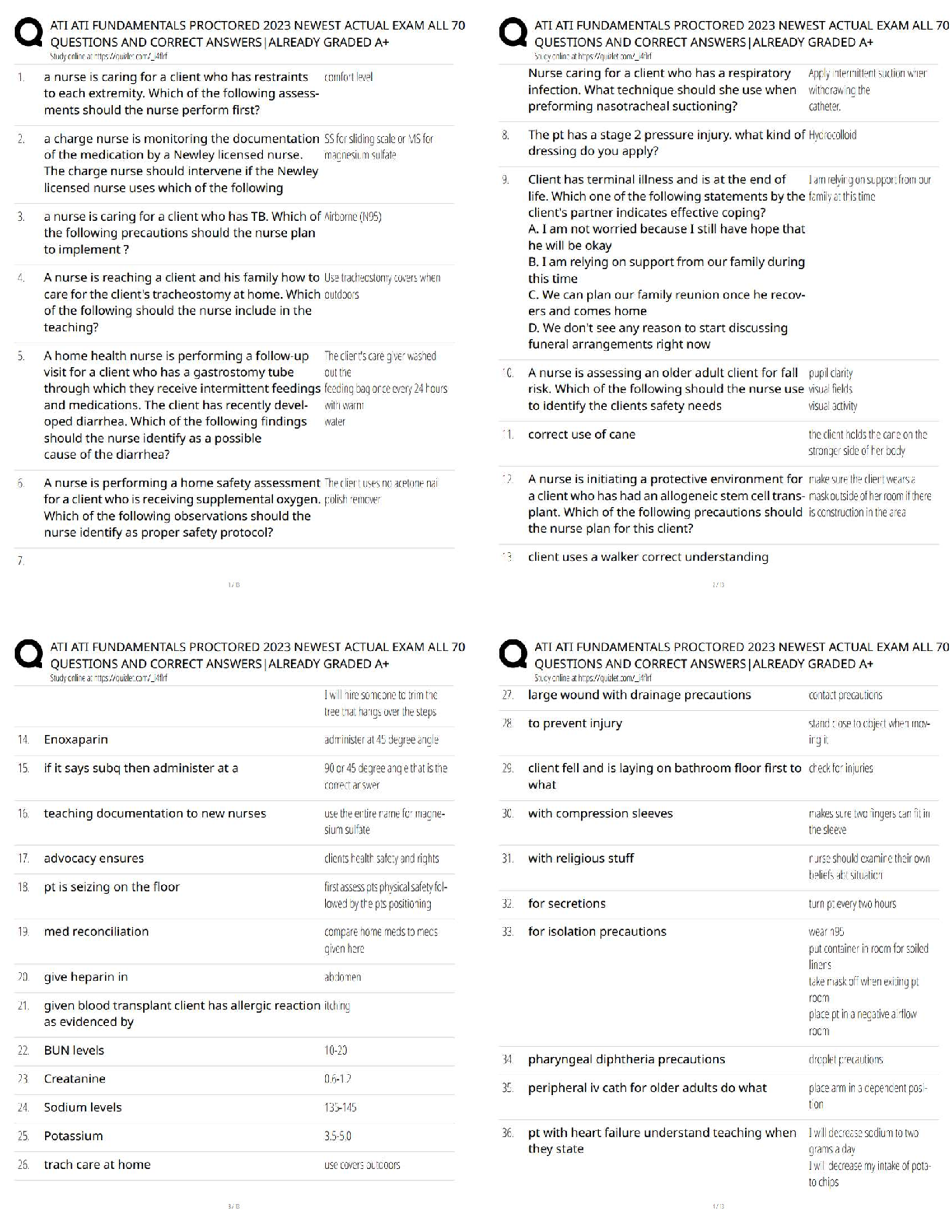
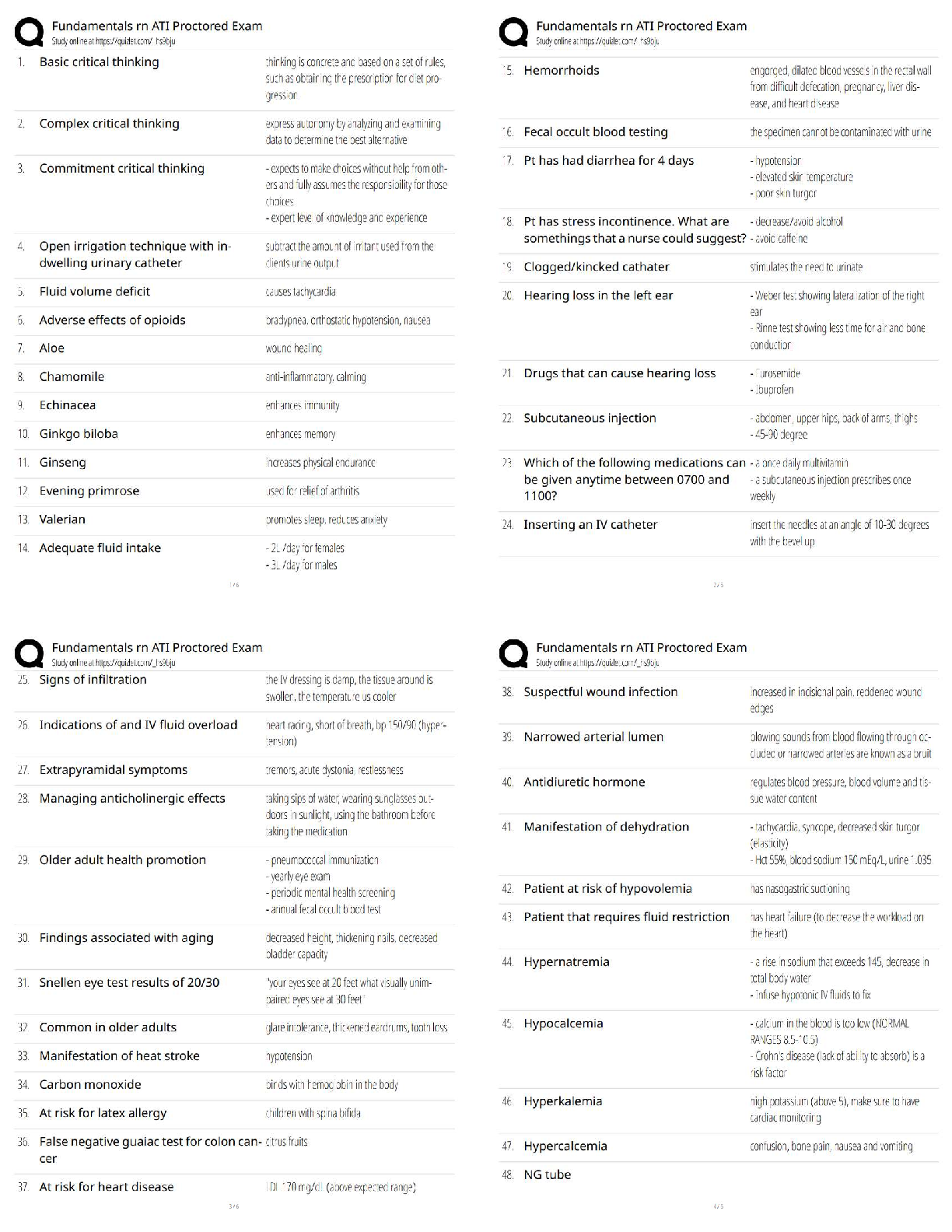
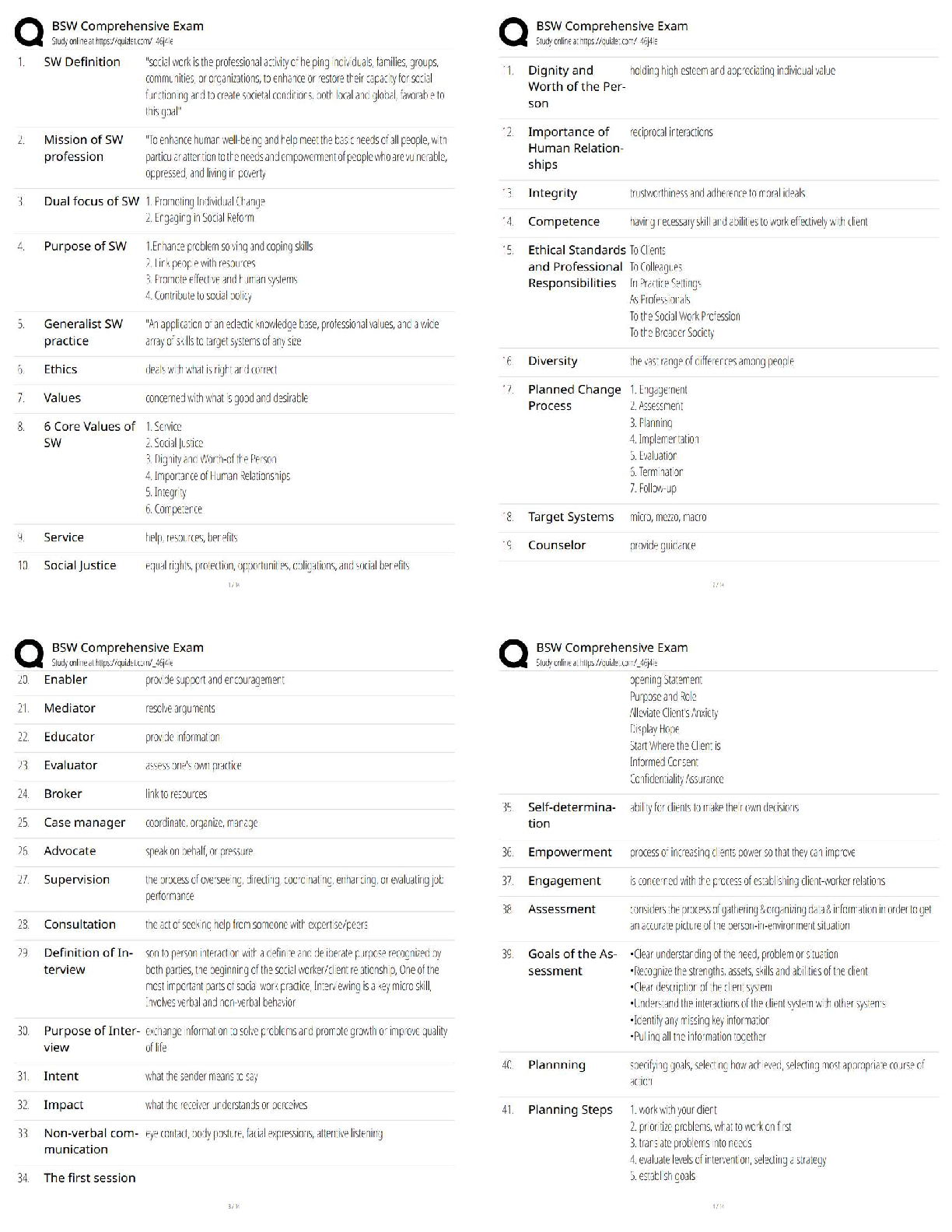
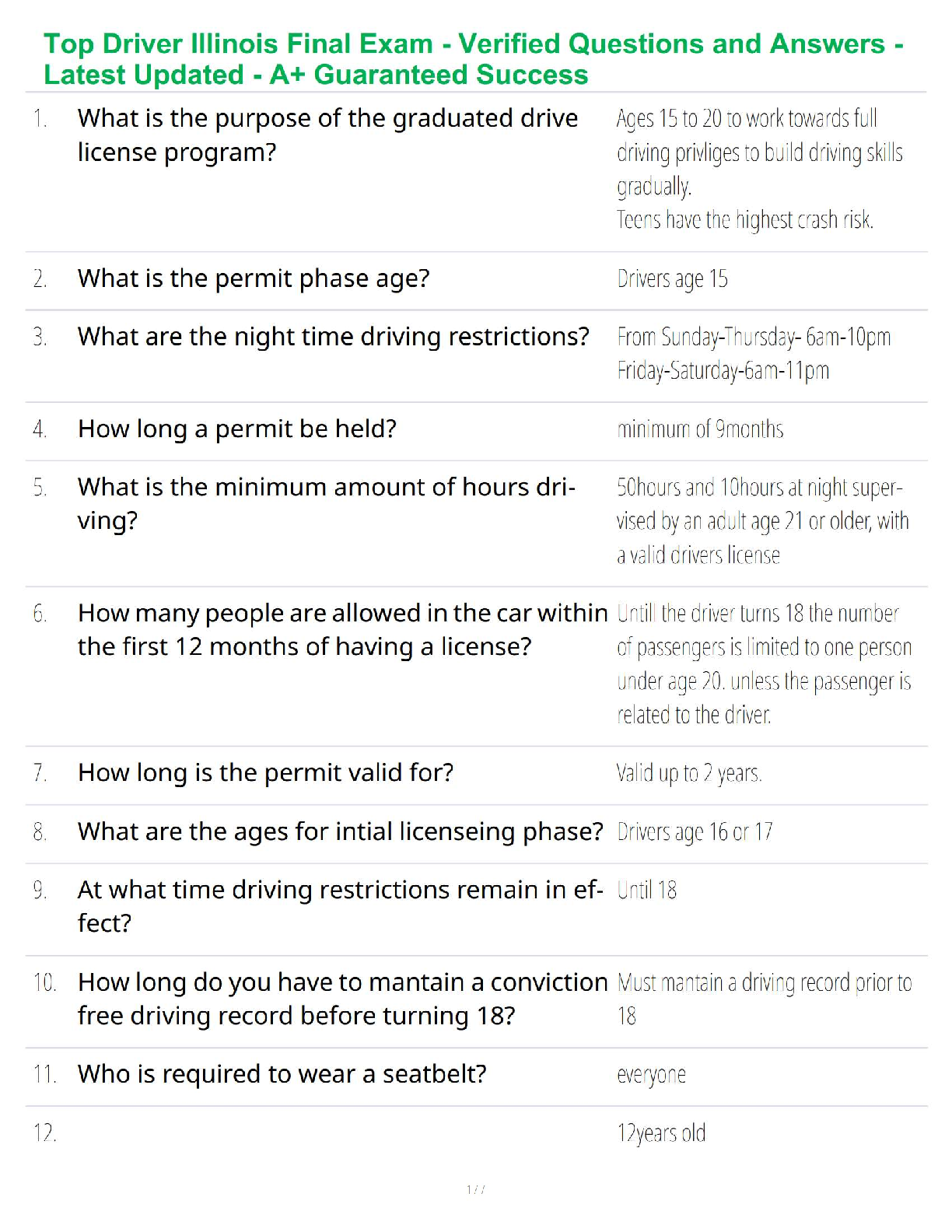
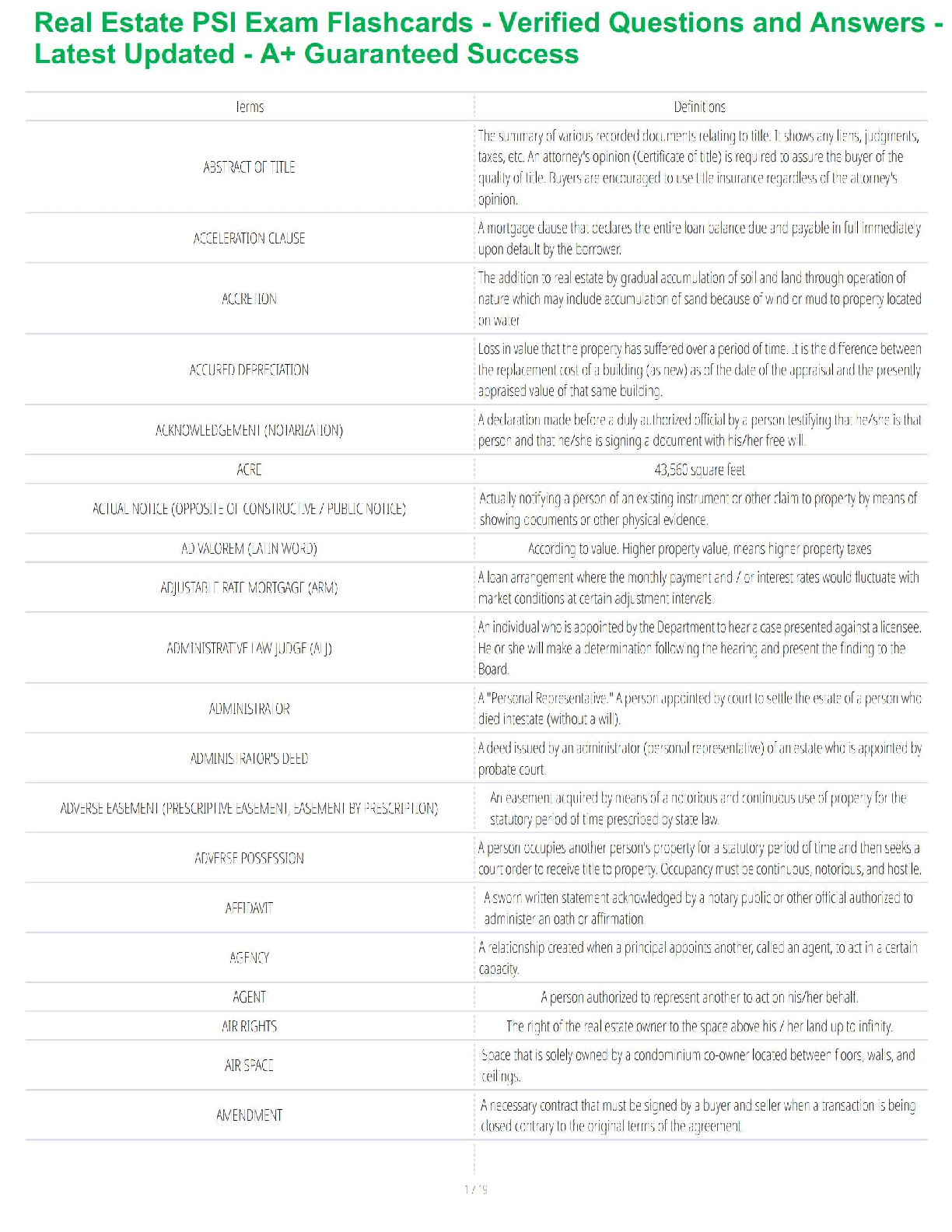
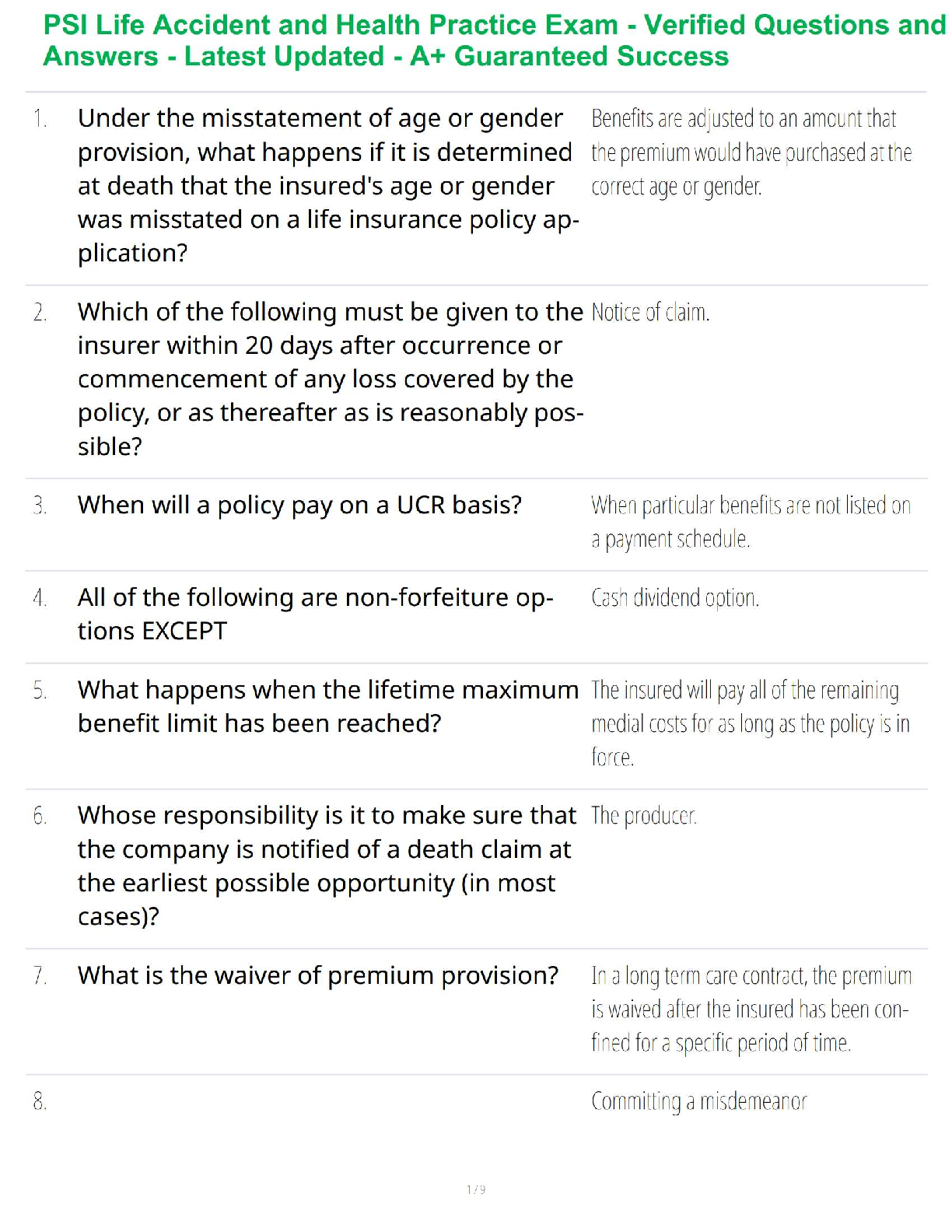
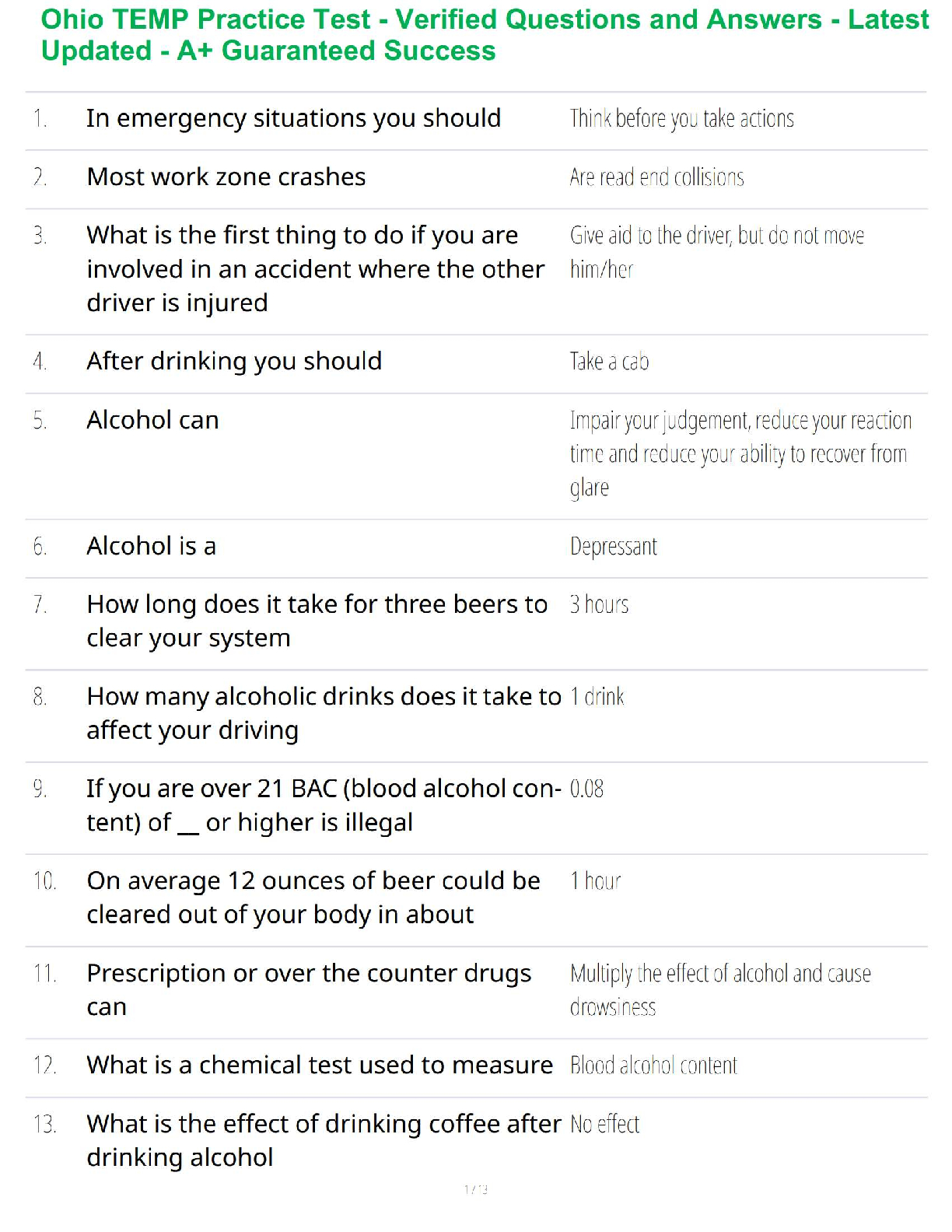
[40 pts] A large water tank empties slowly through a small hole under the force of
gravity. The flow is steady, and the volumetric flow rate ??̇ (in m3/s) depends on the exit velocity
V, the gravitational acceleration
...
[40 pts] A large water tank empties slowly through a small hole under the force of
gravity. The flow is steady, and the volumetric flow rate ??̇ (in m3/s) depends on the exit velocity
V, the gravitational acceleration g, the depth of the water h, and the diameter of the hole D. the
viscosity µ, and the surface tension σ (force/unit length).
(a) Express the nondimensional volumetric flow rate ??̇ in terms of its dependence on the
other nondimensional groups.
(b) A test is to be made on a 1/4th scale model. What is the ratio of the model volumetric
flow rate to the prototype volumetric flow rate that would be needed to obtain dynamical
similarity?
(c) (i) If you now decide that, instead of the volumetric flow rate, you are interested in
the mass flow rate ??̇ , and the density ?? must therefore be included in the
dimensional analysis, will the number of nondimensional groups change?
(ii) Without going through the full derivation again, use the results of part (a) to
express the nondimensional mass flow rate ??̇ in terms of its dependence on the
other nondimensional groups.
(d) If you later discover that the mass flow rate ??̇ depends on the viscosity ?? and the surface
tension ?? (dimensions of force per unit length), in addition to ??, ??, ??, ℎ, and ??, find the
mass flow rate ??̇ in terms of its dependence on the other nondimensional groups. Hint:
you may avoid the full Buckingham Pi derivation by using the nondimensional groups
from part (c) and compiling additional groups with “new” variables and “old” repeating
variables simply by inspection.
Solution:
(a) ??̇ = ??(??, ??, ℎ, ??). N=5 variables.
Denote L=length, T=time, we have
[??̇] =
L3
T
[ℎ] = L; [??] = L; [??] =
L T
; [??] =
L 2T
.
Of the three fundamental units (mass, length, and time), mass is not present here, so K=2.
Therefore, we should have N-K=3 nondimensional groups.
Select ??, ?? as repeating variables.
Show that we can obtain each fundamental unit with these two variables: [??] = L; �????� = T.
Form the nondimensional Pi products:
Π1 = [????1????1ℎ] = ????1(????−1)??1?? = 1 => ??1 + ??1 + 1 = 0; ??1 = 0 => ??1 = −1
=> Π1 =
ℎ ??
.
Π2 = [????2????2??] = ????2(????−1)??2????−2 = 1 => ??2 + ??2 + 1 = 0; −??2 − 2 = 0
=> ??2 = 1; ??2 = −2 => Π2 = ????−2?? = ????
??2 .
[Show More]