Homework 2
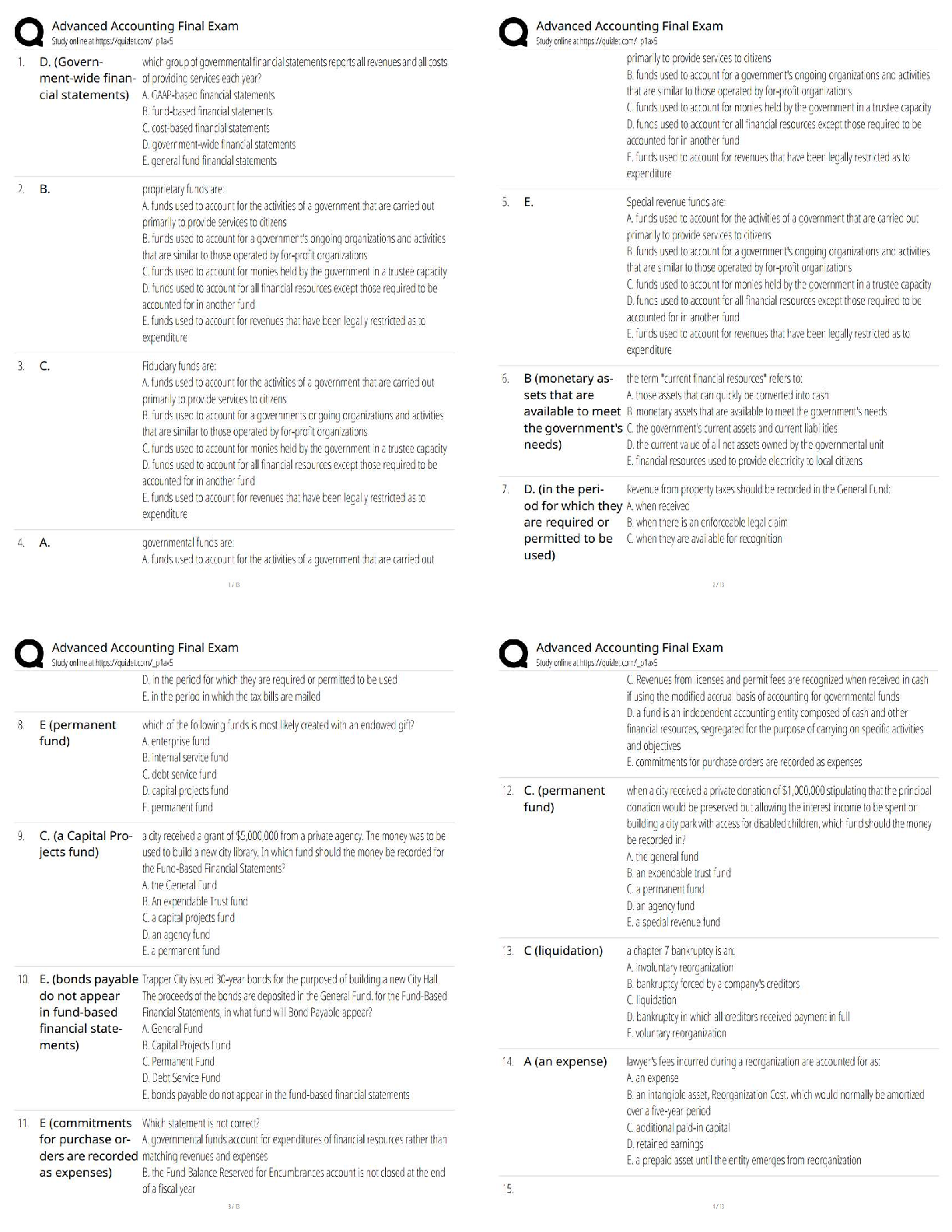
Problem 1 (10 points): A 12-bit ADC has an input range of 1 V to 4 V. If the output of the ADC is 300,
what is the estimated voltage at its input? (ignore quantization error)
Solution: V′ = Emin + Q. r = 1
...
Homework 2
Problem 1 (10 points): A 12-bit ADC has an input range of 1 V to 4 V. If the output of the ADC is 300,
what is the estimated voltage at its input? (ignore quantization error)
Solution: V′ = Emin + Q. r = 1 + 300. 4−1
212 −1 = 1.22V
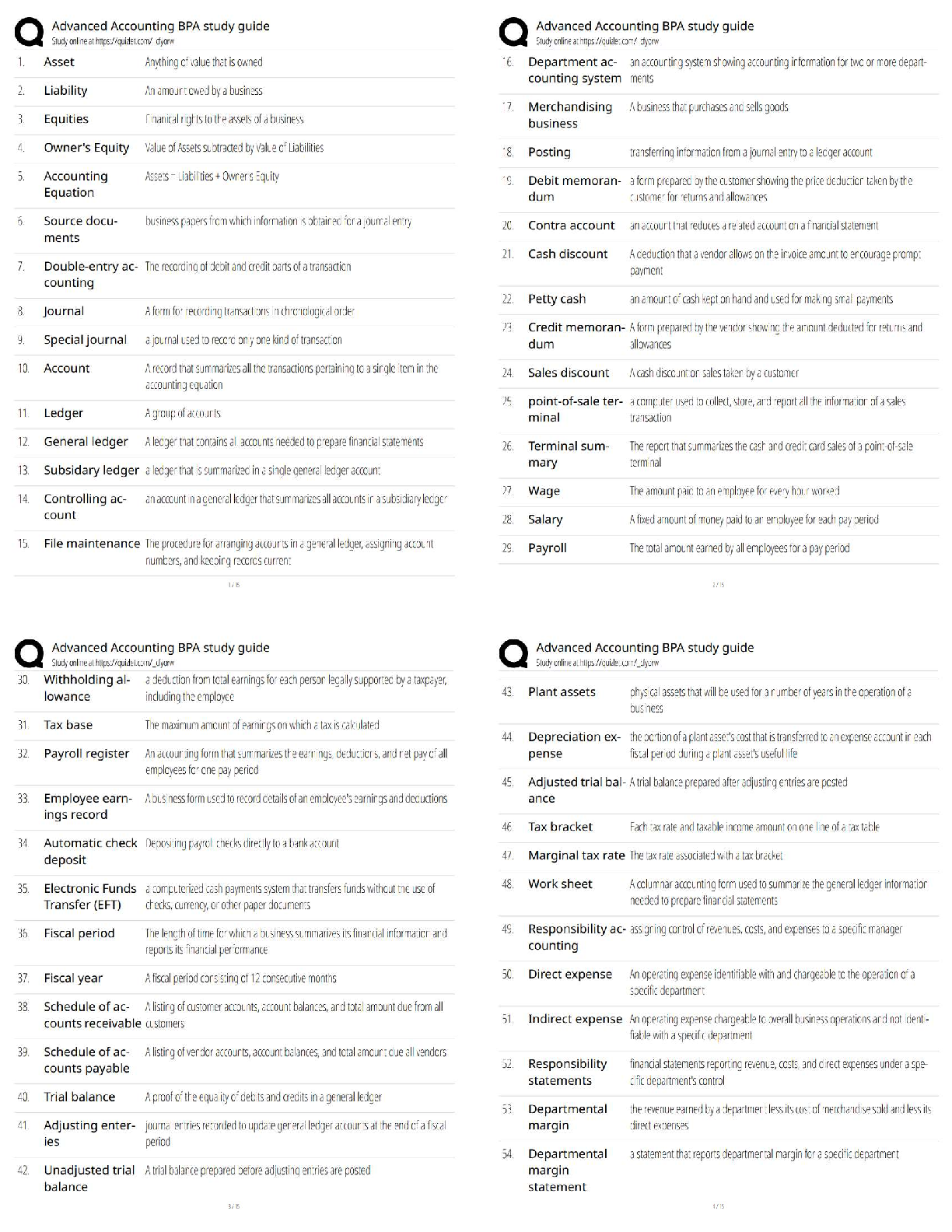
Problem 2 (15 points): A 4-bit ADC has an input range of 2 V to 5 V. At a given instant, if the output of
the ADC is 5,
a) What is the estimated input voltage?
b) What are ?? and ?ℎ , the lower and upper limits of the actual input voltage (taking quantization
error into account)?
Solution:
a) V′ = Emin + Q. r = 1 + 5. 5−2
24−1 = 3V
b) Q = 5−2
24−1 = 0.2
The actual input voltage must lie within ± Q
2 of the estimated voltage, 3V. Therefore,
?? = 3 − 0.1 = 2.9 V and ?ℎ = 3 + 0.1 = 3.1 V
This study source was downloaded by 100000830919685 from CourseHero.com on 06-19-2022 18:32:35 GMT -05:00
https://www.coursehero.com/file/71862439/HW2solSu20pdf/BMEN 3350 Homework 2
Department of Bioengineering, University of Texas at Dallas Page 2
Problem 3 (15 points):
(a) [3 points] Convert the binary number 100110 to decimal. Show your work.
(b) [3 points] Convert the decimal number 43 to binary. Show your work.
(c) [3 points] How many different binary numbers can you form using 8 bits?
(d) If rounding a number (or expressing it using fewer “significant” digits), you can do so by eliminating
digits starting from the right. For example, 68.32 can be rounded to 68.3 or 68, etc., but not to 8.32
or 0.32. In the binary number 10010110,
[i] [3 points] Which are the three most significant bits (MSB)? (circle one)
a. 100
b. 110
[ii] [3 points] The rightmost bit is called, (circle one)
a. The least significant bit (LSB)
b. The somewhat significant bit (SSB)
Solution:
(a) 100110 = 1 ∗ 25 + 0 ∗ 24 + 0 ∗ 23 + 1 ∗ 22 + 1 ∗ 21 + 0 ∗ 20 = 38
(b) 43 = 1 ∗ 25 + 0 ∗ 24 + 1 ∗ 23 + 0 ∗ 22 + 1 ∗ 21 + 1 ∗ 20 = 101011
(c) 28 = 256
(d) (i) 100
(ii) LSB
[Show More]