Mathematics > QUESTIONS & ANSWERS > PRECALC 10112.6.3 Practice_ Complex Numbers-2. 100% Score_Worked Solutions (All)
PRECALC 10112.6.3 Practice_ Complex Numbers-2. 100% Score_Worked Solutions
Document Content and Description Below
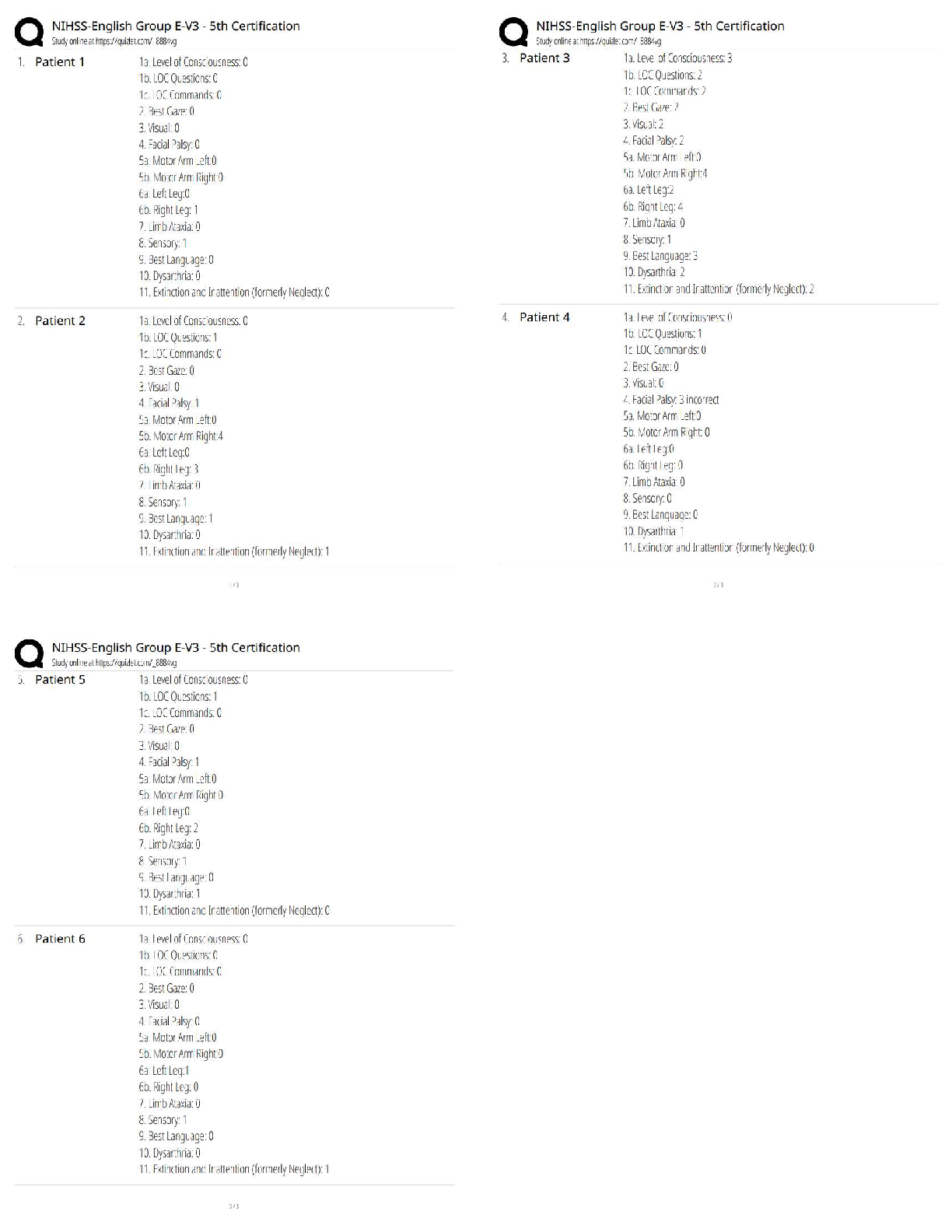
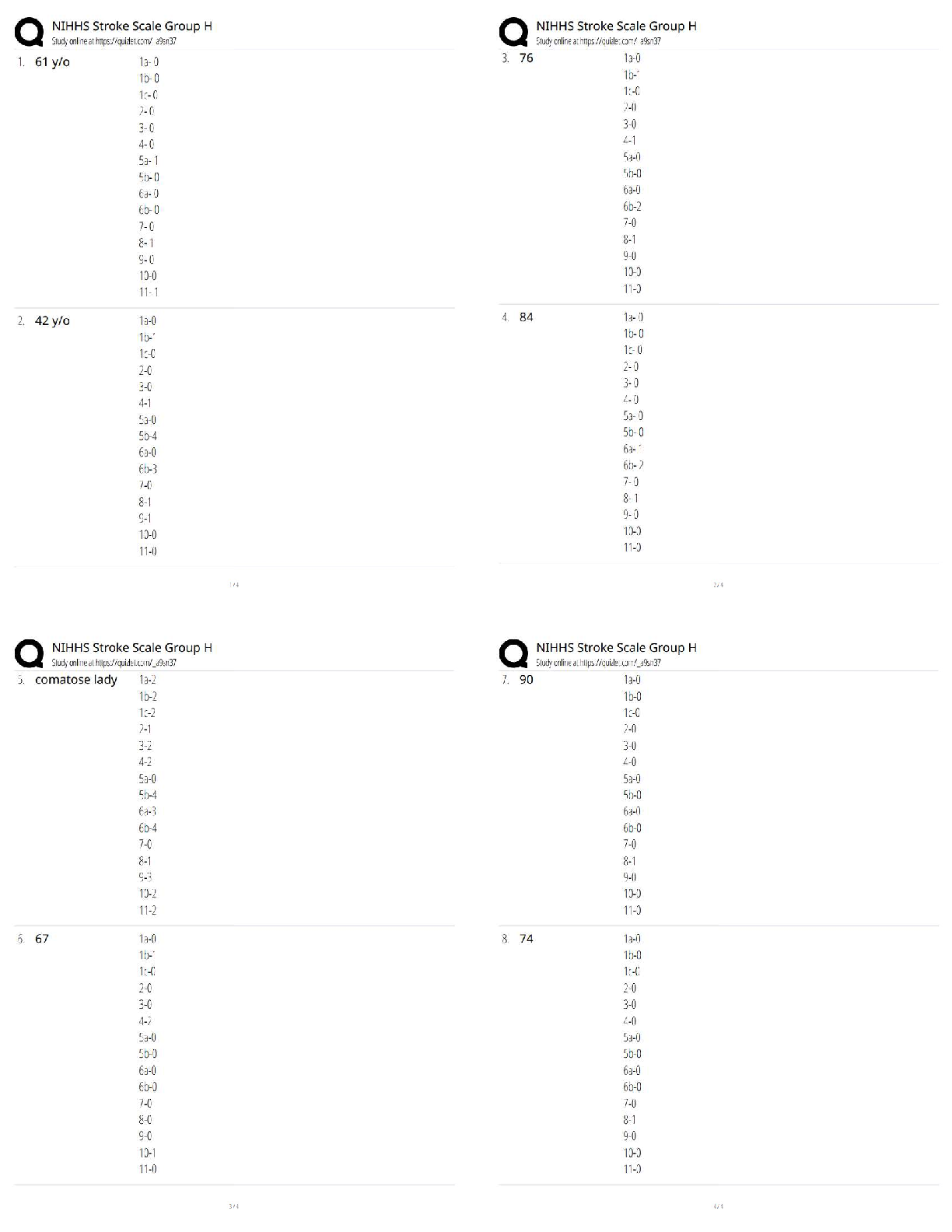
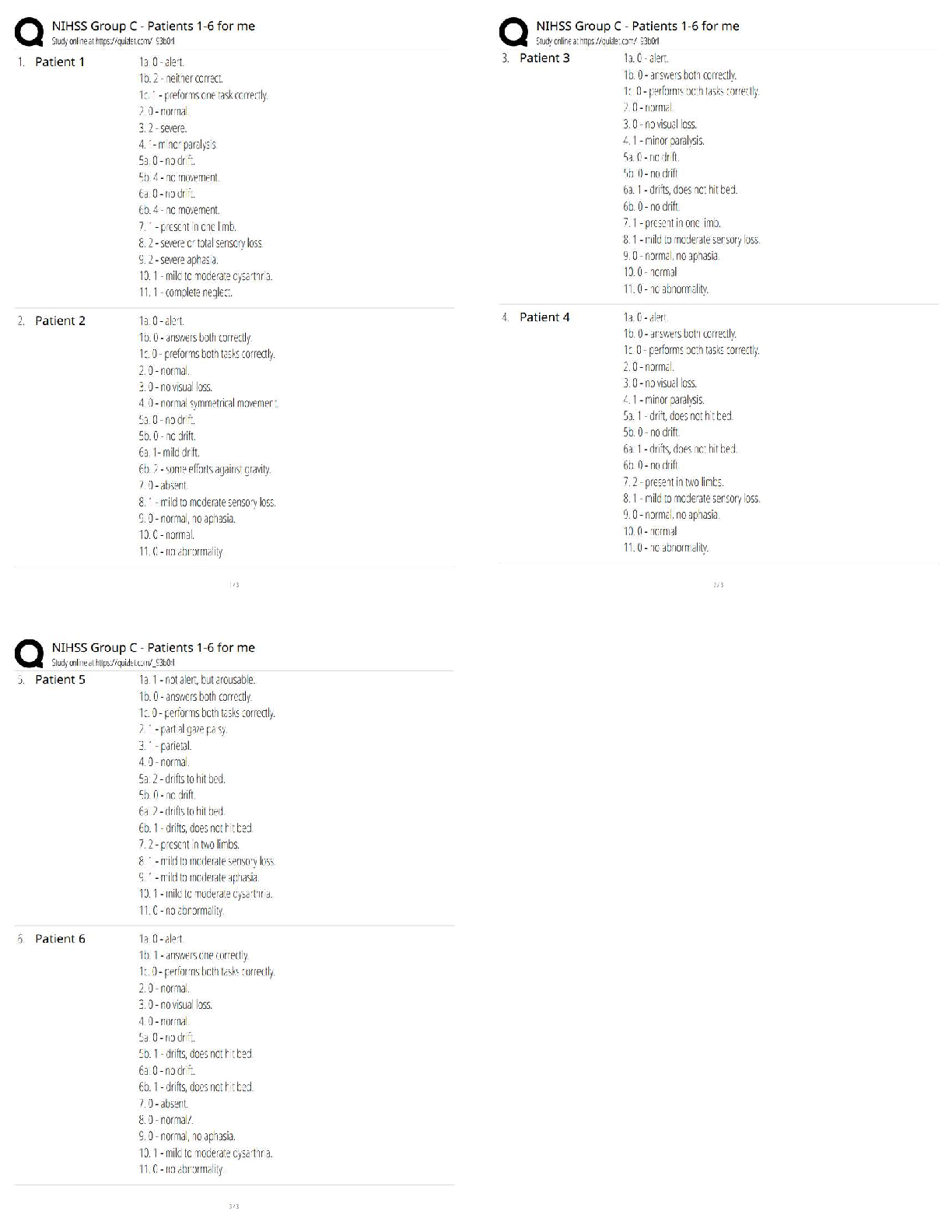
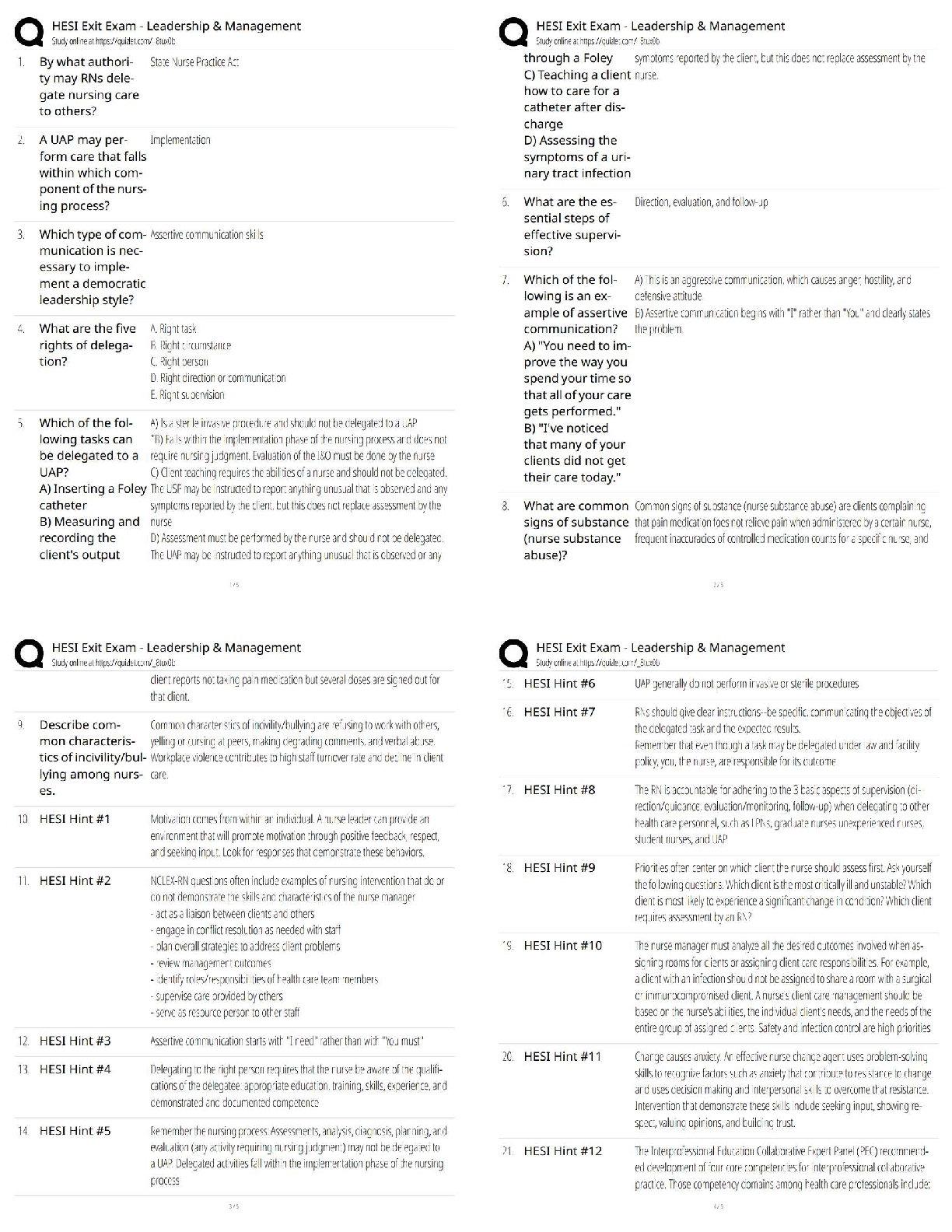
12.6.3 Practice: Complex Numbers Practice Answer the following questions using what you've learned from this unit. Write your responses in the space provided. For questions 1 - 3, the polar coordin ... ates of a point are given. Find the rectangular coordinates of each point. (2 points each) 1. X = rcos ø = 2 cos 3pi/4 = 2 cos pi/2 + pi/4 = -2 sin pi/4 = -2(1/-√2) = --√2 Y = rsinø = 2 sin 3pi/4 = 2 sin pi/2 + pi/4 = 2 cos pi/4 = 2(1/√2) = √2 (-√2, √2) 2. X = rcosø = -4cos 7pi/6 = -4cos (pi + pi/6) = -4(-cos pi/6) = 4cospi/6 = 4(√3/2) = 2√3 Y = rinsinø = -4 sin 7pi/6 = -4sin (pi + pi/6) = -4(-sin pi/6) = 4sinpi/6 = 4 (½) = 2 ( 2√3, 2) 3. X = rcosø =2/3cos (-2pi/3) = ⅔(-½) = -⅓ Y = rsinø = 2/3sin (-2pi/3) =⅔ (-√3/2) = -√3/3 ( -⅓, -√3/3) For questions 4 - 6, the rectangular coordinates of a point are given. Find the polar coordinates of each point. (2 points each) 4. (4, 0) 5. (3, 4) 6. (2, -2) 7. Give two sets of polar coordinates that could be used to plot the given point. (4 points) a. b. 8. Identify, graph, and state the symmetries for each polar equation. Write the scale that you are using for the polar axis. (4 points) a. r = 9cos(5 ) b. r = 2cos 9. Transform each polar equation to an equation in rectangular coordinates and identify its shape. (4 points) a. = 1.34 radians b. r = tan sec 10. Compute the modulus and argument of each complex number. (4 points) a. -5i b. 11. Write each complex number in rectangular form. Plot and label (with a - d) each point on the polar axes below. (4 points) a. b. c. d. 12. Let z = 13 + 7i and w = 3(cos(1.43) + isin(1.43)). (6 points) a. Convert z to polar form. if z= a+bi then in polar form z can be written as z = |r| (cos(θ) + isin(θ)). according to demoivre's theorem :- where and θ = tan-1(b/a). so z = 13+7i = b. Calculate zw using De Moivre's theorem. c. Calculate using De Moivre's theorem. For questions 13 - 15, let and . Calculate the following, keeping your answer in polar form. (2 points each) 13. z1= 2 e^îpi/5 z2= 8 e^i7pi/6 14. z2 = 8( cos 7pi/6-i sin 7 pi/6) 15. z1/z2= 1/4( cos( 29/30)pi-isin(29/30) pi) For questions 16 - 19, write each expression in the standard form for the complex number a + bi. ( 2 points each) 16. 32 + i (32 sqrt 3) 17. 1/32 18. The complex fifth roots of . 10^(1/5)[cos(11pi/30 + 8pi/5) + i sin(11pi/30 + 8pi/5)] 19. Find all seventh roots of unity and sketch them on the axes below. [Show More]
Last updated: 3 years ago
Preview 1 out of 9 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$5.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Aug 03, 2022
Number of pages
9
Written in
All
Additional information
This document has been written for:
Uploaded
Aug 03, 2022
Downloads
0
Views
173