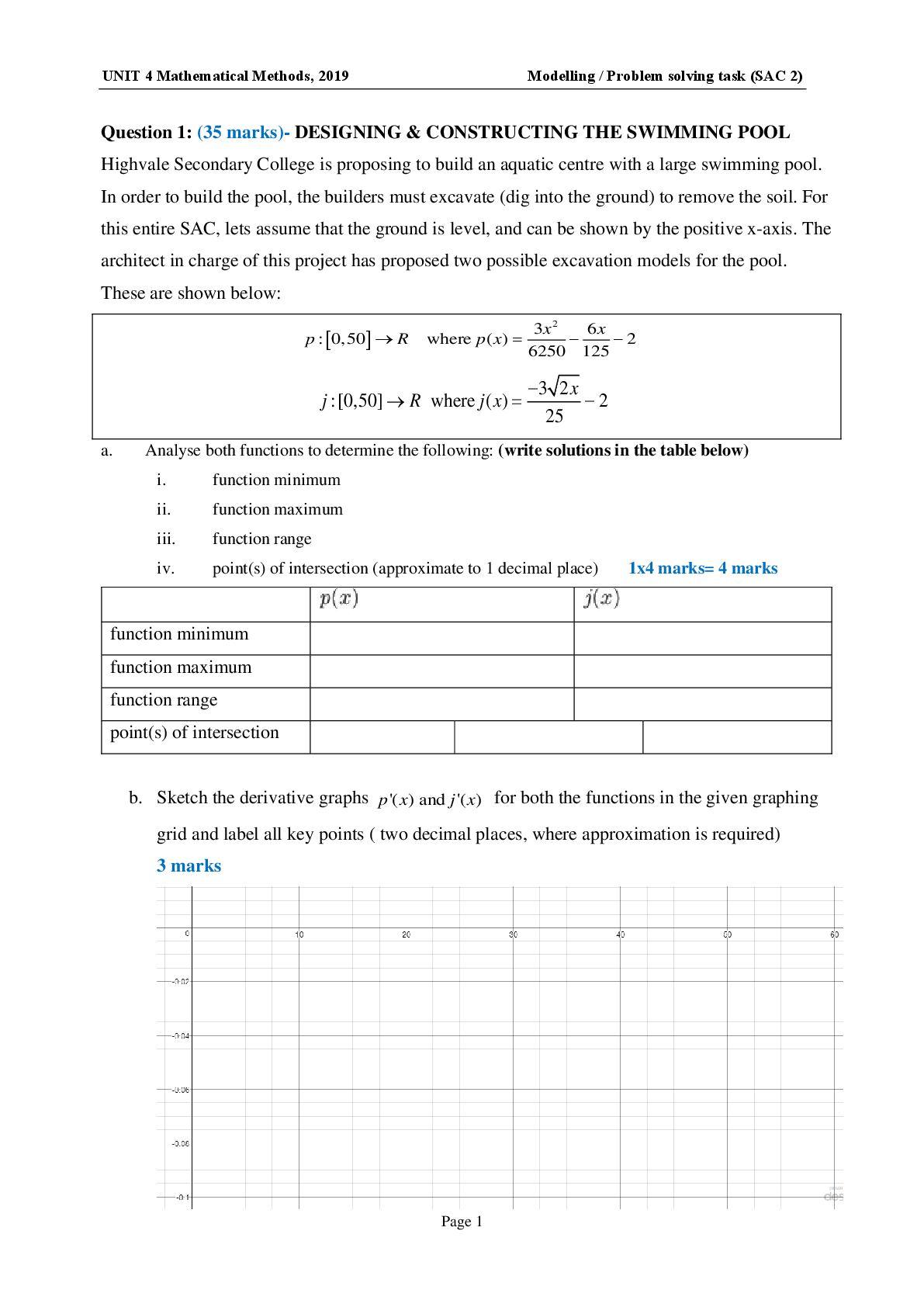
MATHEMATICAL METHODS UNIT 4 School Assessed Coursework 2 (SAC 2):
Modelling Task 1 (Calculus)
Introduction
The Coca-Cola Company wish to begin production at a new manufacturing facility. The facility uses a
3-D p
...
MATHEMATICAL METHODS UNIT 4 School Assessed Coursework 2 (SAC 2):
Modelling Task 1 (Calculus)
Introduction
The Coca-Cola Company wish to begin production at a new manufacturing facility. The facility uses a
3-D printing technology that prints the bottles based on the input of a mathematical function that
represents the 2-D edge of the bottle as shown below:
The printer then rotates the mathematical function around the x-axis to form a three dimensional
bottle. (the x-axis represents the centre of the bottle and an axis of symmetry)
The label is then embossed onto the bottle using a second manufacturing technique. The label is
shown below:
All measurements are given in millimetres and all values should be given in exact form unless
otherwise stated.
f(x)
Question 1
The following information has been provided regarding the bottle to be manufactured.
It is known that:
• The bottle is made up of 3 pieces that make up a hybrid function
• The bottle is 180mm long
• The bottle has two local minimums at (30, 20) and (180, 12)
• The bottle has two local maximums at (0, 24) and (100, 26)
a. If x = 0 represents the base of the bottle and x = 180 the bottles opening, determine
the diameter of the base and the opening of the bottle.
b. Using circular functions of the form:
?? = ??. sin�??(?? - ??)� + ??
Find the function f(x) that models the edge of the bottle in the following form using the
given domains for each piece
??(??) = �??????321(((??????))),,, 100 300≤≤≤??????<≤<100 180 30
c. Explain, in terms of the gradient at specific points, why each of the three joins in the
function from part b. are considered smooth
d. Sketch the function from part b. showing all intercepts, stationary points and end
points
It is decided to explore a second model for the edge of the bottle made up this time of three
second order polynomials of the form:
?? = ??(?? - ℎ)2 + ??
For the second model it is known that:
• The bottle is made up of 3 pieces that make up a hybrid function
• The bottle is 180mm long
• The bottle has two local minimums at (30, 20) and (180, 12)
• The bottle has one local maximum at (100, 26)
• A smooth join between the second and third piece of the hybrid function is
located at x = 145
• The other join between the first and second pieces of the hybrid function is also
smooth but its location is unknown
[Show More]