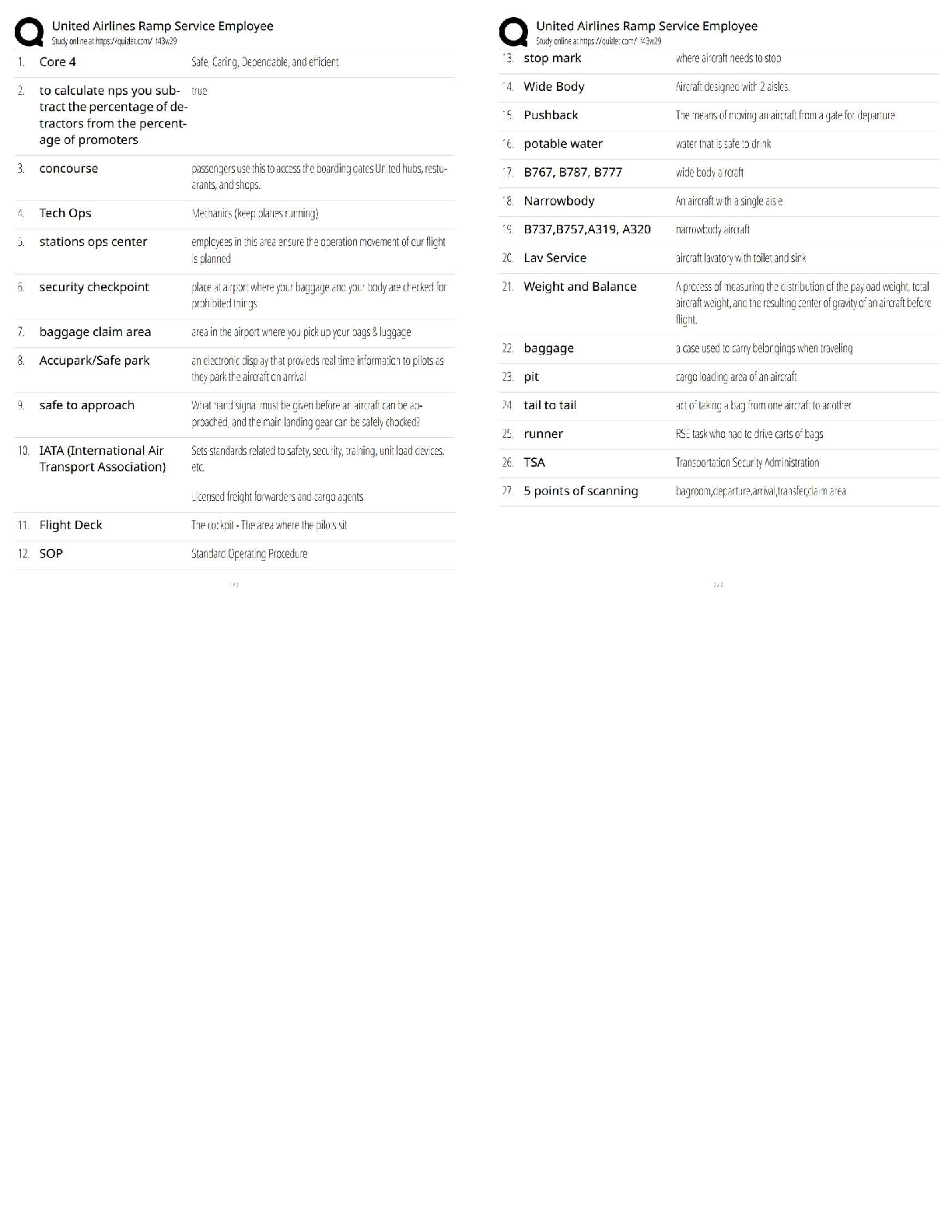
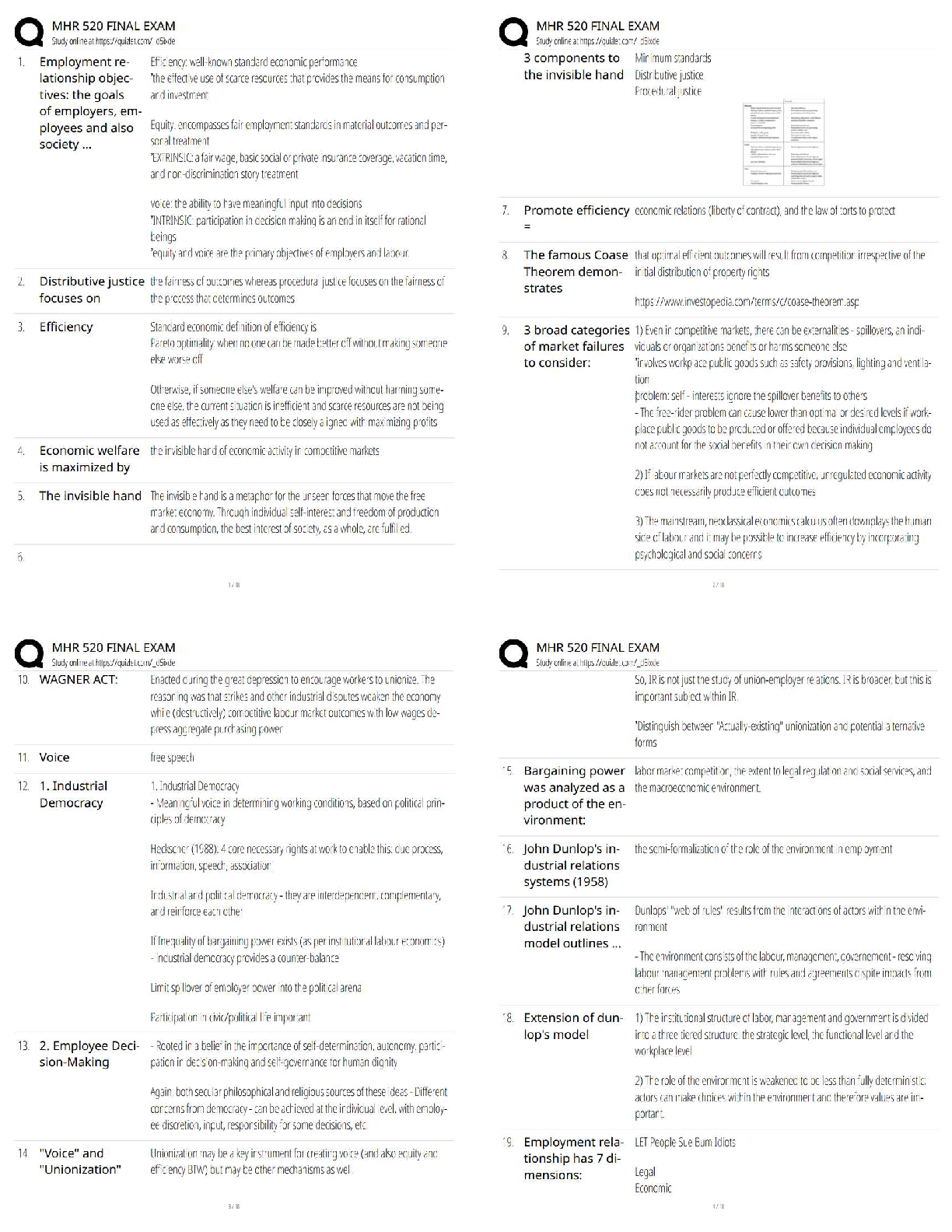
The length of time a person takes to decide which shoes to purchase is normally distributed with a mean
of 8.54 minutes and a standard deviation of 1.91. Find the probability that a randomly selected
individual will ta
...
The length of time a person takes to decide which shoes to purchase is normally distributed with a mean
of 8.54 minutes and a standard deviation of 1.91. Find the probability that a randomly selected
individual will take less than 6 minutes to select a shoe purchase. Is this outcome unusual?
Probability is 0.91, which is unusual as it is greater than 5%
Probability is 0.09, which is unusual as it is less than 5%
Probability is 0.09, which is usual as it is not less than 5%
Probability is 0.91, which is usual as it is greater than 5%
The length of time a person takes to decide which shoes to purchase is normally distributed with a mean
of 8.21 minutes and a standard deviation of 1.90. Find the probability that a randomly selected
individual will take less than 6 minutes to select a shoe purchase. Is this outcome unusual?
Probability is 0.12, which is usual as it is not less than 5%
Probability is 0.88, which is usual as it is greater than 5%
Probability is 0.12, which is unusual as it is less than 5%
Probability is 0.88, which is unusual as it is greater than 5%
Monthly water bills for a city have a mean of $108.43 and a standard deviation of $36.98. Find the
probability that a randomly selected bill will have an amount greater than $173, which the city believes
might indicate that someone is wasting water. Would a bill that size be considered unusual?
Probability is 0.04, which is usual as it is not less than 5%
Probability is 0.04, which is unusual as it is less than 5%
Probability is 0.04, which is unusual as it is not less than 5%
Probability is 0.04, which is usual as it is less than 5%
Monthly water bills for a city have a mean of $108.43 and a standard deviation of $36.98. Find the
probability that a randomly selected bill will have an amount greater than $173, which the city believes
might indicate that someone is wasting water. Would a bill that size be considered unusual?
Probability is 0.04, which is usual as it is less than 5%
Probability is 0.04, which is usual as it is not less than 5%
Probability is 0.04, which is unusual as it is not less than 5%
Probability is 0.04, which is unusual as it is less than 5%
In a health club, research shows that on average, patrons spend an average of 46.2 minutes on the
treadmill, with a standard deviation of 4.8 minutes. It is assumed that this is a normally distributed
variable. Find the probability that randomly selected individual would spent between 30 and 40 minutes
on the treadmill.
0.10
0.90
0.80
-0.10
In a health club, research shows that on average, patrons spend an average of 42.5 minutes on the
treadmill, with a standard deviation of 4.8 minutes. It is assumed that this is a normally distributed
variable. Find the probability that randomly selected individual would spent between 30 and 40 minutes
on the treadmill.
0.30
Less than 1%
0.40
0.70
A tire company measures the tread on newly-produced tires and finds that they are normally distributed
with a mean depth of 0.98mm and a standard deviation of 0.35mm. Find the probability that a randomly
selected tire will have a depth less than 0.50mm. Would this outcome warrant a refund (meaning that it
would be unusual)?
Probability of 0.09 and would warrant a refund
Probability of 0.91 and would not warrant a refund
Probability of 0.91 and would warrant a refund
Probability of 0.09 and would not warrant a refund
[Show More]