Questions and Answers > LS 30A: MATHEMATICS FOR LIFE SCIENTISTS FALL 2017 - LECTURE 1. MIDTERM SOLUTIONS

Document Content and Description Below

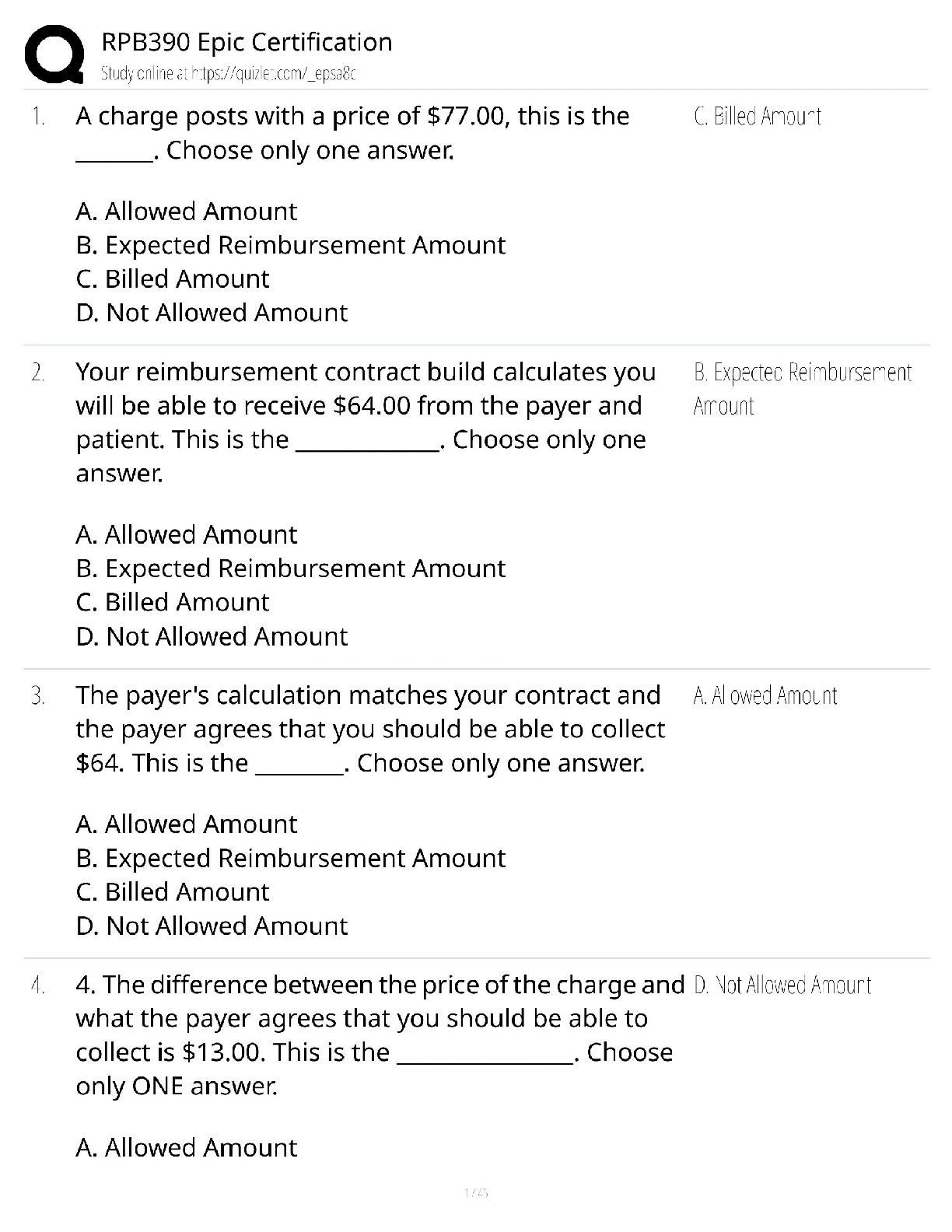
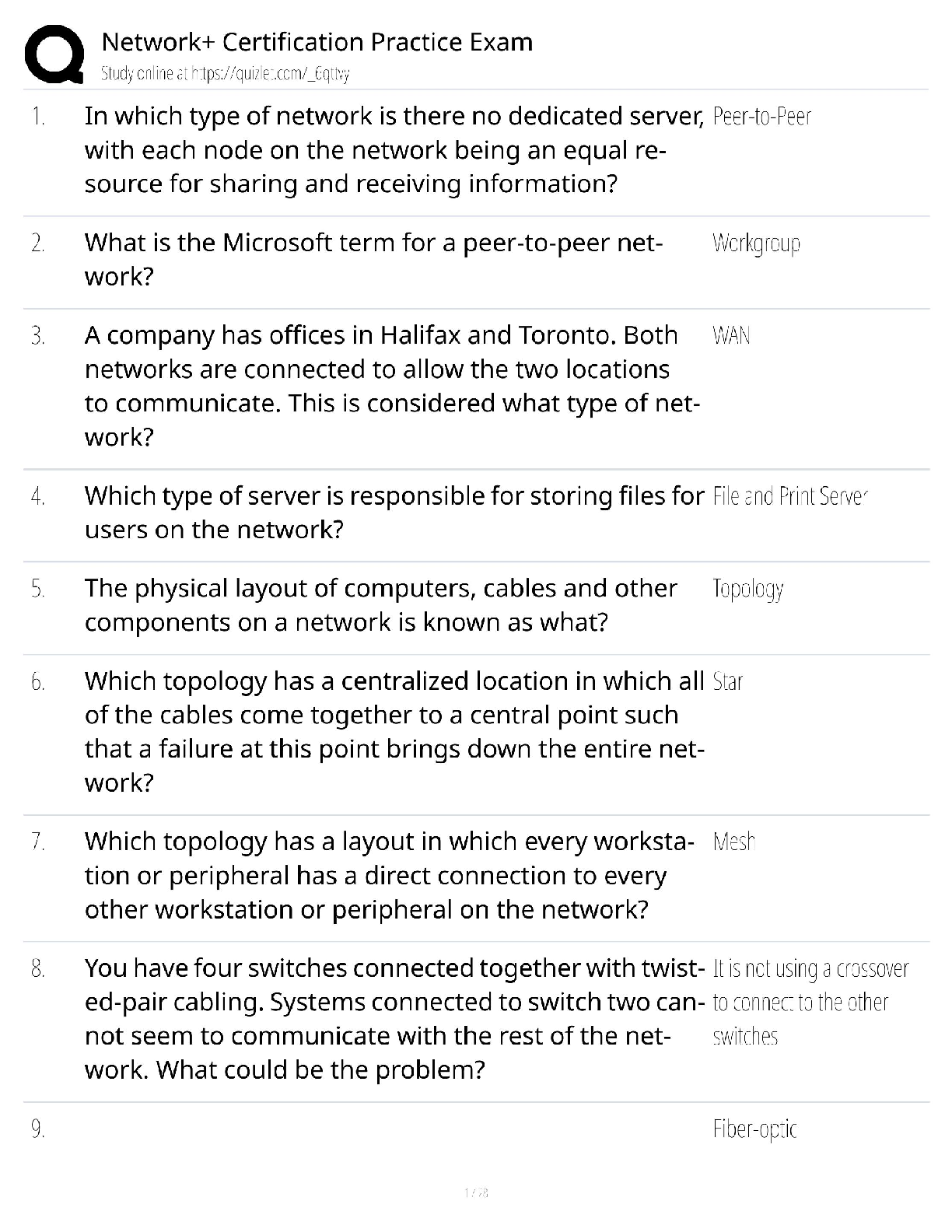
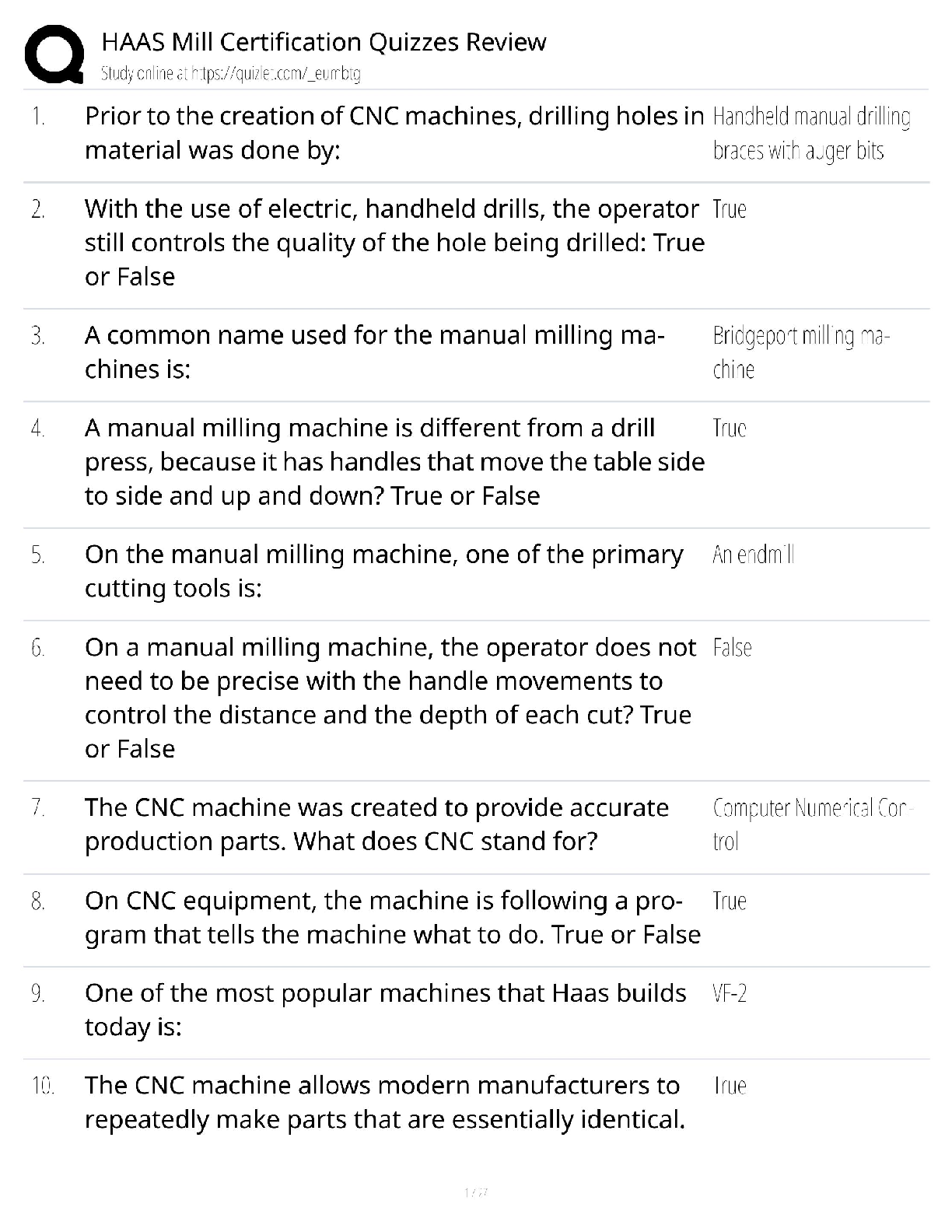
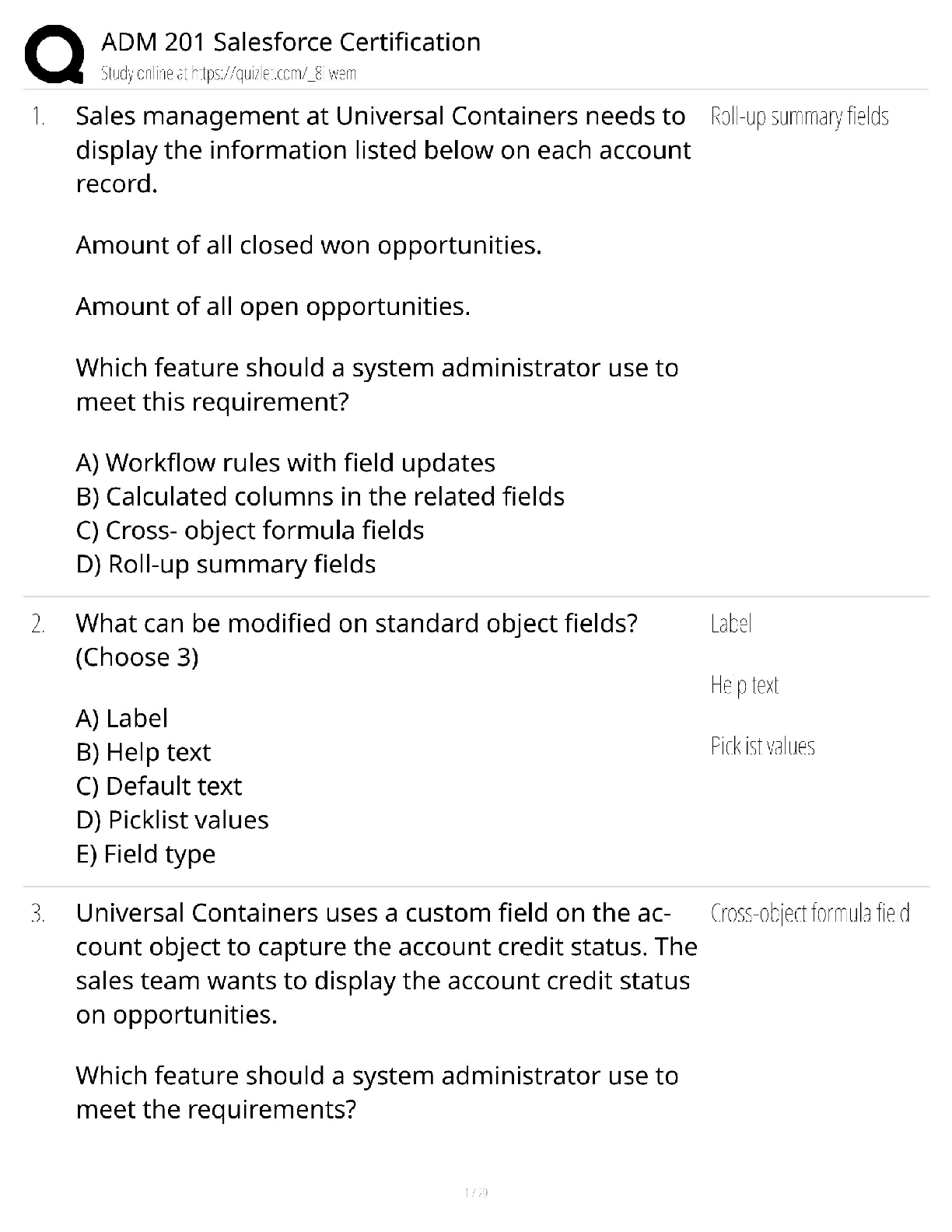
LS 30A: MATHEMATICS FOR LIFE SCIENTISTS FALL 2017 - LECTURE 1. MIDTERM SOLUTIONS LS 30A: MATHEMATICS FOR LIFE SCIENTISTS FALL 2017 - LECTURE 1 MIDTERM SOLUTIONS Your Name Your Student ID nu ... mber Your TA Section By signing below, you confirm that you did not cheat on this exam. No exam booklet without a signature will be graded. INSTRUCTIONS • Please do not open this booklet until you are told to do so. • In addition to basic writing instruments, you are allowed to use a non-programmable calculator. • Your cell phone must be turned off completely and stowed away where you cannot see it. • No books or notes. • If you have a question at any time during the exam, please raise your hand. • You will receive points only for work written on the numbered pages. Please use the reverse side as scratch paper. • Make sure to write legibly. Illegible work will not be graded. • Make sure to show all your work and justify your answers fully. TOTAL 1. (10 pts) Raccoons inhabit the UCLA campus. Write down a differential equation for the number R of raccoons living at the UCLA campus, using the following assumptions. 1. Every year, m raccoons come from the Santa Monica Mountains and join the UCLA population. 2. The raccoon per capita birth rate is proportional to the number of trash cans, c (their primary food source), with a constant of proportionality b. 3. The raccoon per capita death rate is proportional to the ratio of the number of raccoons to the number of trash cans, with a constant of proportionality d. 4. Every year, s raccoons emigrate from the UCLA campus to the USC campus. 2. a) (3 pts) Draw a flow chart for the UCLA student population, using the following assumptions. Introduce further parameters as necessary. 1. Every student is either a 1st-year student (F), a 2nd-year student (S), a 3rd-year student (T), or a 4th-year student (L). 2. Every year, UCLA receives a certain number applications for admission; call this number a. 3. The UCLA admission rate is p percent. 4. Of the admitted applicants, q percent choose to attend UCLA. 5. Every student starts out as a 1st-year student. 6. A student can graduate only as a 4th-year student. 7. Every year, a certain fraction of students in each year level fail to advance to the next year level; to advance from the 4th year level means that that you graduate. You may assume that it is the same fraction for all year levels. 8. Of those who fail to advance, a certain fraction will leave UCLA without a degree, while the rest will remain at their current level for another year. You may assume that it is the same fraction for all year levels. 2 b) (5 pts) Write down a model for the UCLA student population, using the assumptions on the previous page. For each parameter of your model, indicate the range of its possible values. ns of the sets): 1 pt c) (2 pts) By using the notation from the first two parts of this problem, write down an equation representing the condition that the overall student population is neither growing nor declining. 3. (10 pts) In a certain town, there lives a population of N nerds. The nerds patronize comic book stores, of which there are C in this town. The nerds are harassed by mean hipsters, of which there are H. Write down a model for the nerd-hipster-comic book store system, using the following assumptions. • Since comic book stores rely on nerds for business, the rate at which new comic book stores are opened is proportional to the number of nerds, with a proportionality constant of 0.001. • Pairs of hipsters amuse themselves by making fun of comic book stores, negatively affecting the image of the stores. So, comic book stores go out of business at a per store rate proportional to the likelihood of two hipsters running into each other in front of a store, with a proportionality constant of 0.002. • Nerds enjoy living in a town with many other nerds and many comic book stores, so nerds move into town at a rate proportional to the number of nerds times the number of comic book stores, with a proportionality constant of 0.03. • Nerds move out of town due to being hired by Google at a per capita rate of 0.04 per year. • In addition, each year, nerds move out of town in order to get away from the hipsters at a per capita rate proportional to the number of hipsters, with a proportionality constant 0.05. • Hipsters like to live in a town with few comic book stores, so hipsters move into town at a rate proportional to the reciprocal of the number of comic book stores, with a proportionality constant of 0.06. • Hipster dislike living in a town with many nerds, so hipsters move out of town at a per capita rate proportional to the number of nerds, with a proportionality constant of 0.07. • Every once in a while, a hipster walks into a comic book store by chance, likes what they find in there, and becomes a nerd. The probability of a hipster liking what they find in a comic book store is 0.0008. 4 4. a) (2 pts) By using the concepts we have learned in this course, state the definition of a vector field. The phrase (or any reasonable permutation of) \function from the state space into the tangent space": 1 pt The concrete description in terms of the change vectors: 1 pt b) (8 pts) Let R be Romeo’s love for Juliet (or hate if negative), and let J be Juliet’s love for her Romeo (or hate if negative). Assume that the Romeo-Juliet system is modeled by J R00 = 0 = 0::25JR+ 0 - 0::41RJ2 Compute eight vectors from the vector field of this model with -4 6 J 6 4 and -4 6 R 6 4. Then draw those vectors in the diagram provided on the next page. Spread them out so as to give a reasonable representation of the field. 5 Draw your vectors here: 6 5. a) (2 pts) State the formula for Euler’s method in the case the number n of state variables is 2. What I am hoping to see here is an explicit recognition that points have two coordinates and vectors have two components. Nevertheless, any reasonable statement of Euler’s method: 2 pts. b) (8 pts) Recall the \Shark-Tuna" model of a predator-prey system: ST00 == ST T --ST S where S represents the number of sharks (predators) and T represents the number of tuna (prey). Suppose that a system modeled by the Shark-Tuna model starts at an initial state, at time t = 0 years, in which there are 2 sharks and 3 tuna. Use Euler’s method, with a time increment ∆t = 0:1 years, to approximate the numbers of sharks and tuna at time t = 0:2 years. Full partial credit may be given for a relatively correct second stage answer based on an incorrect first stage answer. 7 6. a) (1 pt) State the definition of the derivative of F = F (X) with respect to X at X = a: b) (1 pts) Explain how the definition you gave in part a) is related to the average rate of change of F near the point (a; F (a)). Any reasonable rephrasing of the above: 1 pt c) (2 pts) State both forms of the formula for linear approximation in terms of F (X) and X. 2) F (b) ≈ F (a) + dF dX X=a∆X Each form: 1 pt 8 d) (3 pts) By using only the definition you stated in part a) of this problem, find the derivative of F (X) = 3X2 + 4X + 5 with respect to X at X = 1. e) (3 pts) By using your answers to parts c) and d) of this problem, use linear approximation to estimate F (1:1), where F (X) is the polynomial from part d). [Show More]

Last updated: 3 years ago

Preview 1 out of 10 pages