STAT 200 Week 4 Homework Problems Complete Guide 100% CORRECT {2020/2021}

Document Content and Description Below

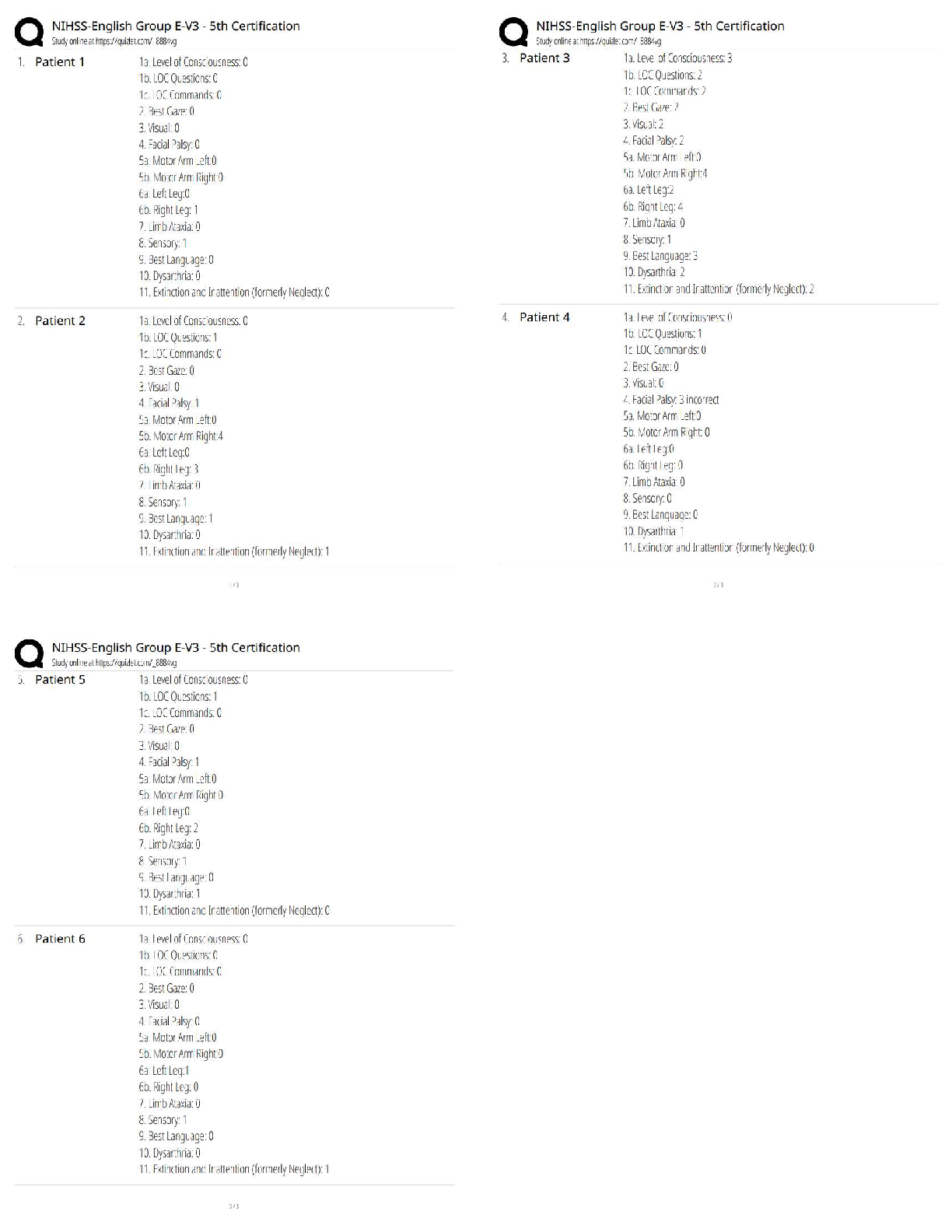
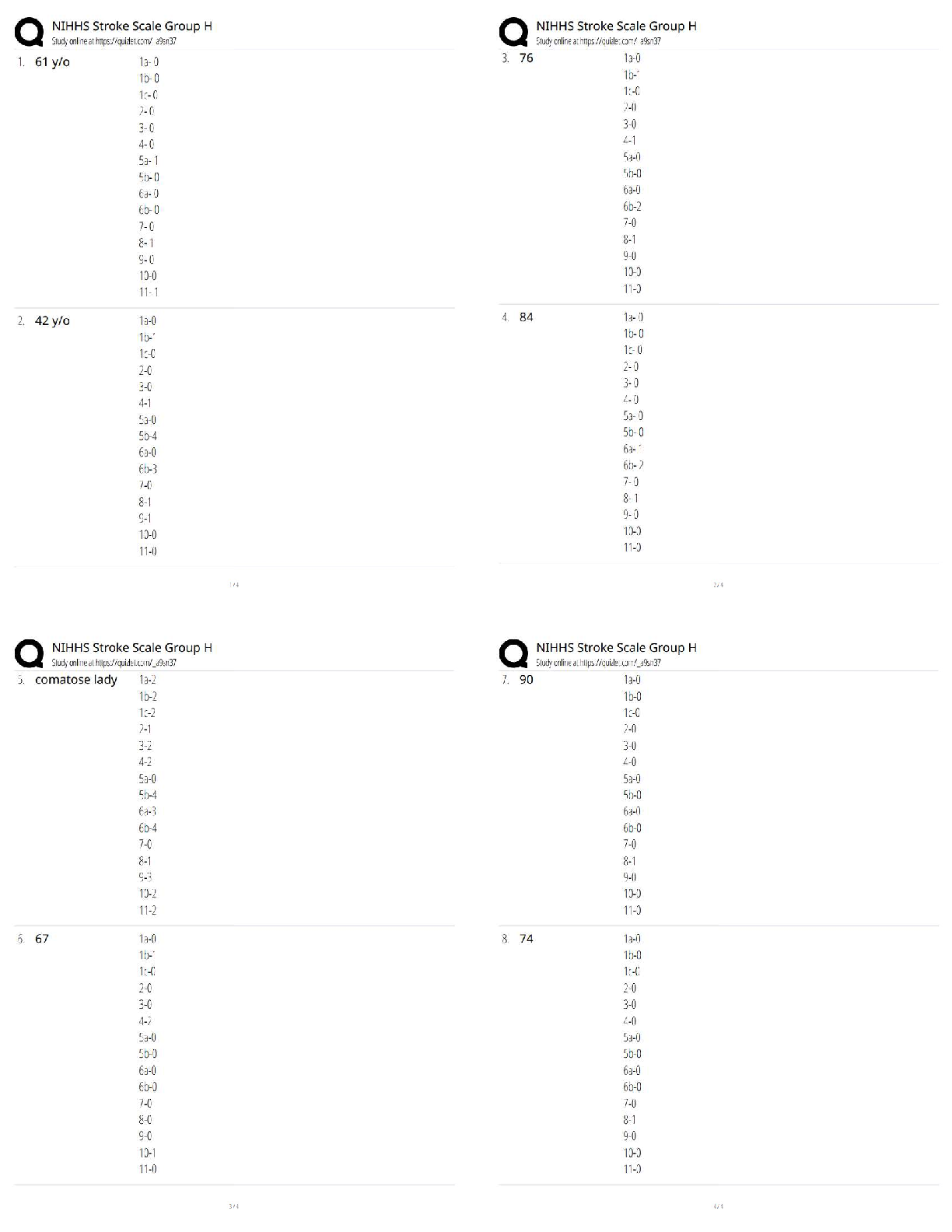
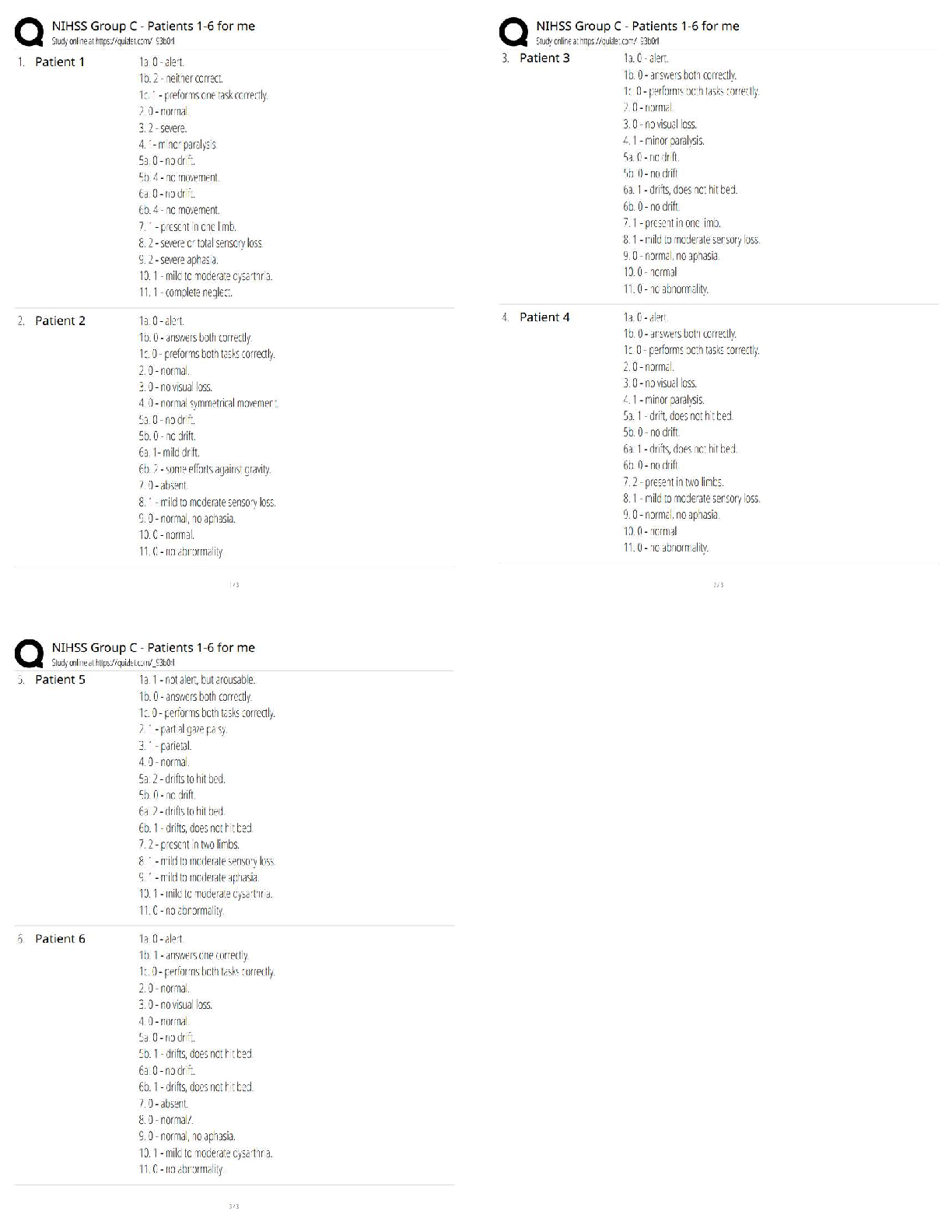
STAT 200 Week 4 Homework Problems 6.1.2 1.) The commuter trains on the Red Line for the Regional Transit Authority (RTA) in Cleveland, OH, have a waiting time during peak rush hour periods of eigh ... t minutes ("2012 annual report," 2012). a.) State the random variable. The random variable is the waiting time. b.) Find the height of this uniform distribution. c.) Find the probability of waiting between four and five minutes. d.) Find the probability of waiting between three and eight minutes. e.) Find the probability of waiting five minutes exactly. P(Waiting time = exactly 5) = 0,000 6.3.2 Find the z-score corresponding to the given area. Remember, z is distributed as the standard normal distribution with mean of  = 0 and standard deviation  = 1. a.) The area to the left of z is 15%. -1.04 b.) The area to the right of z is 65%. -0.385 c.) The area to the left of z is 10%. -1.282 d.) The area to the right of z is 5%. 1.645 e.) The area between z and z is 95%. 1.96 f.) The area between z and z is 99%. 2.576 6.3.4 According to the WHO MONICA Project the mean blood pressure for people in China is 128 mmHg with a standard deviation of 23 mmHg (Kuulasmaa, Hense & Tolonen, 1998). Assume that blood pressure is normally distributed. a.) State the random variable. The blood pressure for the people in China. b.) Find the probability that a person in China has blood pressure of 135 mmHg or more. .3804 c.) Find the probability that a person in China has blood pressure of 141 mmHg or less. .7140 d.) Find the probability that a person in China has blood pressure between 120 and 125 mmHg. .0841 e.) Is it unusual for a person in China to have a blood pressure of 135 mmHg? Why or why not? No, its not because the probability is 38%. f.) What blood pressure do 90% of all people in China have less than? 157.48 mmHg. 6.3.8 A dishwasher has a mean life of 12 years with an estimated standard deviation of 1.25 years ("Appliance life expectancy," 2013). Assume the life of a dishwasher is normally distributed. a.) State the random variable. Life of a dishwasher b.) Find the probability that a dishwasher will last more than 15 years. .0082 c.) Find the probability that a dishwasher will last less than 6 years. .0000 d.) Find the probability that a dishwasher will last between 8 and 10 years. .0541 e.) If you found a dishwasher that lasted less than 6 years, would you think that you have a problem with the manufacturing process? Why or why not? .0000 f.) A manufacturer of dishwashers only wants to replace free of charge 5% of all dishwashers. How long should the manufacturer make the warranty period? 9.9 years 6.3.10 The mean yearly rainfall in Sydney, Australia, is about 137 mm and the standard deviation is about 69 mm ("Annual maximums of," 2013). Assume rainfall is normally distributed. a.) State the random variable. Yearly rainfall b.) Find the probability that the yearly rainfall is less than 100 mm. .2964 c.) Find the probability that the yearly rainfall is more than 240 mm. 0.0681 d.) Find the probability that the yearly rainfall is between 140 and 250 mm. .4335 e.) If a year has a rainfall less than 100mm, does that mean it is an unusually dry year? Why or why not? .05 f.) What rainfall amount are 90% of all yearly rainfalls more than? 49 mm 6.4.4 Annual rainfalls for Sydney, Australia are given in table #6.4.6. ("Annual maximums of," 2013). Can you assume rainfall is normally distributed? Table #6.4.6: Annual Rainfall in Sydney, Australia 146.8 383 90.9 178.1 267.5 95.5 156.5 180 90.9 139.7 200.2 171.7 187.2 184.9 70.1 58 84.1 55.6 133.1 271.8 135.9 71.9 99.4 110.6 47.5 97.8 122.7 58.4 154.4 173.7 118.8 88 84.6 171.5 254.3 185.9 137.2 138.9 96.2 85 45.2 74.7 264.9 113.8 133.4 68.1 156.4 6.5.2 A random variable is normally distributed. It has a mean of 245 and a standard deviation of 21. a.) If you take a sample of size 10, can you say what the shape of the distribution for the sample mean is? Why? The shape of the distribution for the sample mean is symmetric bell shaped. b.) For a sample of size 10, state the mean of the sample mean and the standard deviation of the sample mean. c.) For a sample of size 10, find the probability that the sample mean is more than 241 d.) If you take a sample of size 35, can you say what the shape of the distribution of the sample mean is? Why? The shape of the distribution for the sample mean is symmetric or bell shaped because the sample size increases. e.) For a sample of size 35, state the mean of the sample mean and the standard deviation of the sample mean. f.) For a sample of size 35, find the probability that the sample mean is more than 241. g.) Compare your answers in part c and f. Why is one smaller than the other? C. Because one is asking for a sample size of 10 the other is asking for a sample size of 35. 6.5.4 According to the WHO MONICA Project the mean blood pressure for people in China is 128 mmHg with a standard deviation of 23 mmHg (Kuulasmaa, Hense & Tolonen, 1998). Blood pressure is normally distributed. a.) State the random variable. The person in China’s blood pressure. b.) Suppose a sample of size 15 is taken. State the shape of the distribution of the sample mean. c.) Suppose a sample of size 15 is taken. State the mean of the sample mean. 128 d.) Suppose a sample of size 15 is taken. State the standard deviation of the sample mean. 5.938 e.) Suppose a sample of size 15 is taken. Find the probability that the sample mean blood pressure is more than 135 mmHg. .1192 f.) Would it be unusual to find a sample mean of 15 people in China of more than 135 mmHg? Why or why not? Yes because its greater than the sample mean of 128. g.) If you did find a sample mean for 15 people in China to be more than 135 mmHg, what might you conclude? That a possible mistake in data. 6.5.6 The mean cholesterol levels of women age 45-59 in Ghana, Nigeria, and Seychelles is 5.1 mmol/l and the standard deviation is 1.0 mmol/l (Lawes, Hoorn, Law & Rodgers, 2004). Assume that cholesterol levels are normally distributed. a.) State the random variable. Cholesterol of the person. b.) Find the probability that a woman age 45-59 in Ghana has a cholesterol level above 6.2 mmol/l (considered a high level). 0 [Show More]

Last updated: 3 years ago

Preview 1 out of 5 pages