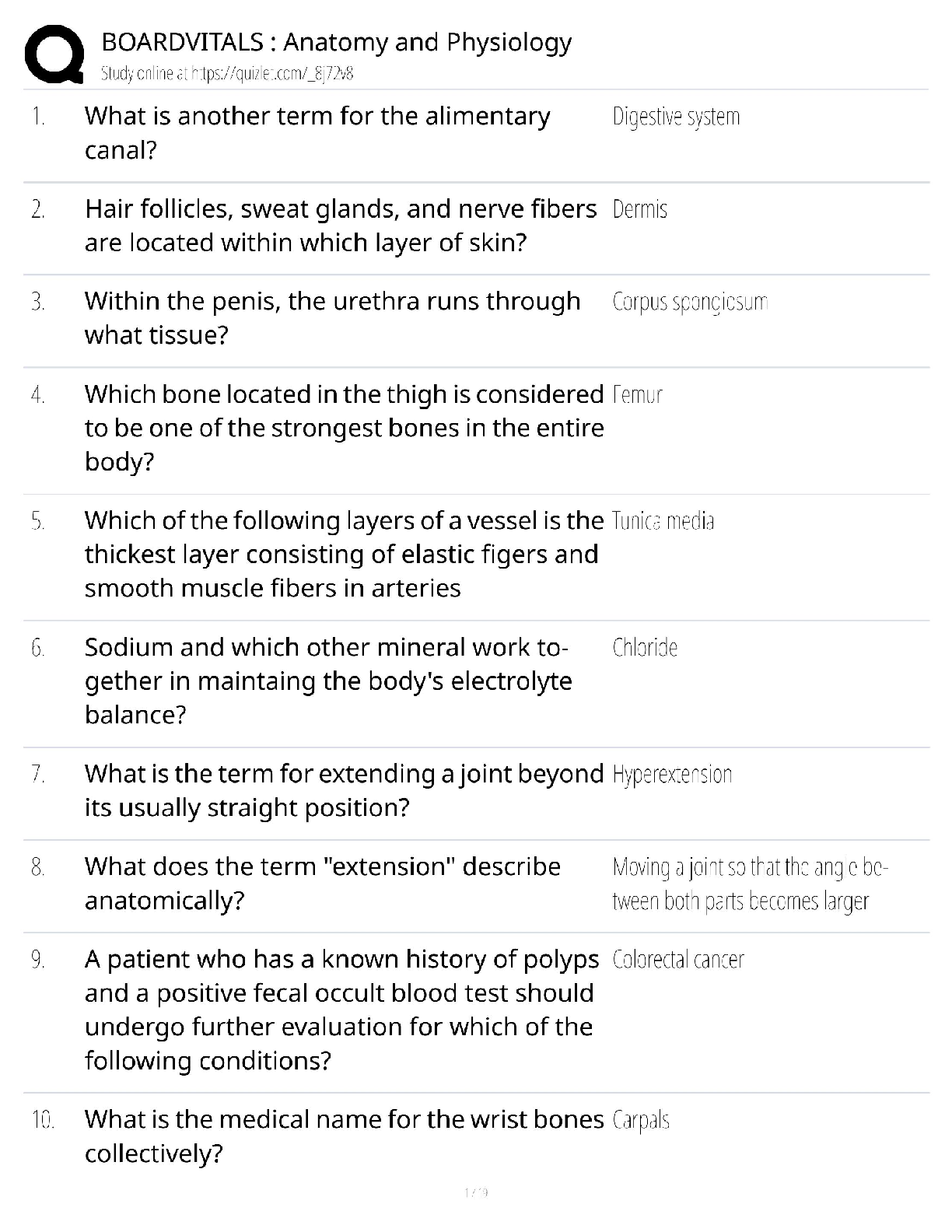
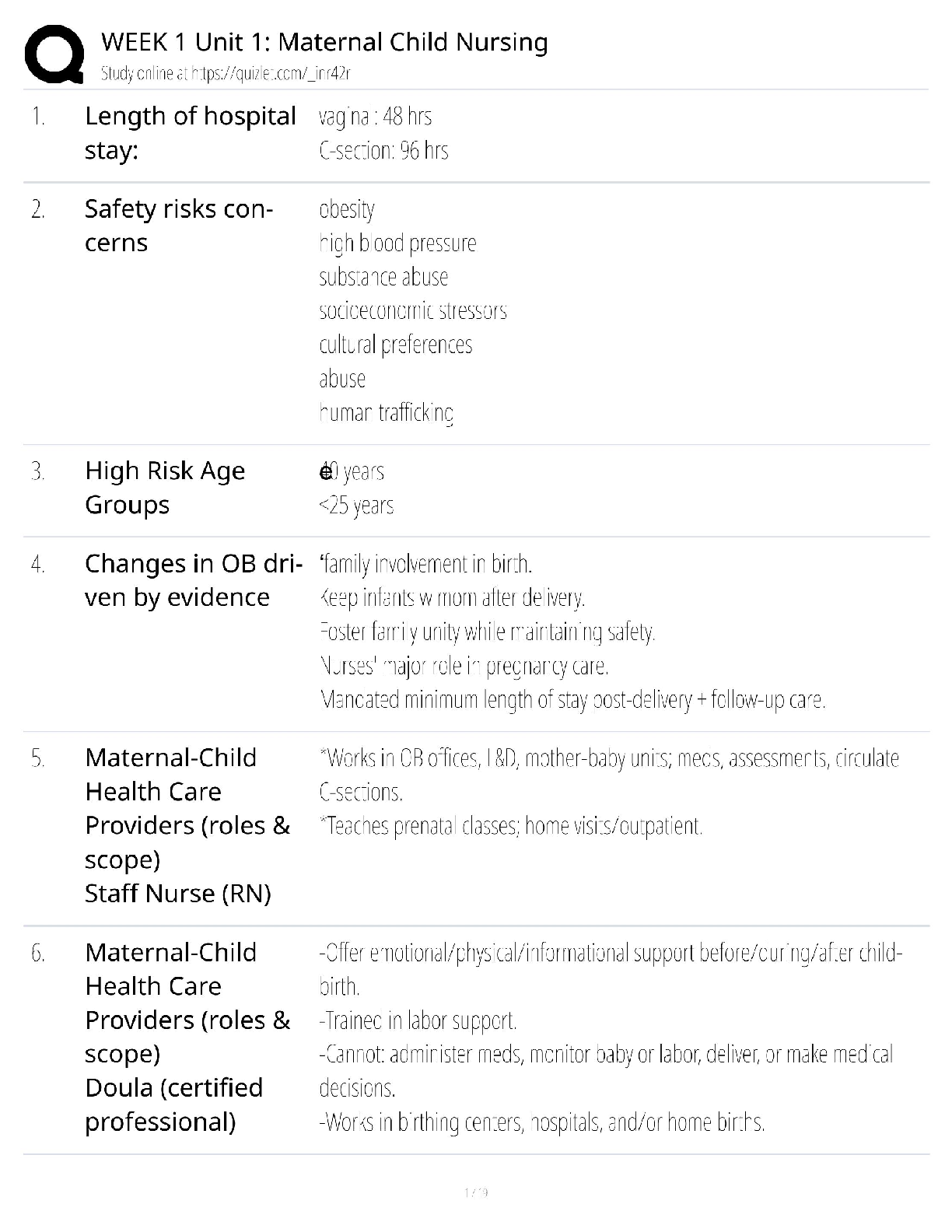
MIS 589 WEEK 6 QUIZ QUESTIONS ANS ANSWERS
$ 13

RN ATI COMPREHENSIVE PREDICTOR EXIT EXAM FINAL VERSION 2024 WITH NGN (90% Score)
$ 65

Software Engineering A Practitioner's Approach 9th Edition By Roger Pressman, Bruce Maxim | Test Bank All Chapters, 100% Original Verified
$ 25

Mark Scheme (Results) June 2022 Pearson Edexcel GCSE In Computer Science (1CP2/01) Paper 1: Principles of Computer Science Edexcel and BTEC Qualifications
$ 8

Harvard University {Data analytics Quizzes , BUSINESS CORE} questions and answer 100 % correct | kindly contact +1 (681) 229 7738 for any academic assistance.
$ 44

Java Foundations Introduction to Program Design and Data Structures, 5th edition John Lewis Test Bank
$ 22

Art_History_Unit 1 Milestone 1
$ 7.5

Instructor Solutions Manual for Physics, Volume 2 5th Edition by Robert Resnick, All Chapters 1-24.
$ 13
.png)
WGU C715 Organizational Behavior Questions and Answers 100% Pass
$ 10

PYC 1501 Study notes Fall 2019 - University of South Africa / PYC1501 Study notes Fall 2019 - University of South Africa
$ 2.5

Northern Virginia Community College - MUSIC 121Study Guide - Exam 2.
$ 7

SOPHIA UNIT 1 Philosophy_Milestone 1 Exam 100% CORRECT ANSWERS | DeVry University
$ 11

Experience Human Development By Diane Papalia and Gabriela Martorell
$ 24

APEA 3P Actual Exam Test Bank (APEA Question Bank) (Mostly Resourceful) APEA A+ Update
$ 9

BIOS-252 Week 4 Case Study Assignment: Autonomic Nervous System (GRADED A)
$ 10

GIZMO - Student Exploration: Sine, Cosine, and Tangent Ratios [Answer Key]
$ 10

VITA Basic Exam | Questions with 100% Correct Answers | Verified | Updated 2025
$ 27.5

HVAC Basics
$ 30.5

PHIL 347 Week 1 - Course Project; Topic Selection - Immigration:
$ 5

eBook Probability and Statistics 4th Edition By Morris H. DeGroot , Mark J. Schervish
$ 30

eBook PDF Electrical Wiring Commercial 17th Edition By Phil Simmons; Ray Mullin
$ 30

ServSafe Food Handler Guide, Chapter 5: Cleaning and Sanitizing
$ 8

University of California, Los Angeles LIFESCIENC 30A. Homework 4 solutions
$ 9

Jackson Weber (Complex).,WELL EXPLAINED 100%CORRECT.
$ 16

AQA A-level PHYSICS 7408/1 Paper 1 Mark scheme June 2021 Version: 1.0 Final
$ 10

2023 AQA GCSE STATISTICS 8382/2F Foundation Tier Paper 2 Question Paper & Mark scheme (Merged) June 2023 [VERIFIED]
$ 7

MICROBIOLOGY PORTAGE - MODULE 4 MICROBIAL GROWTH AND CONTROL EXAM QUESTIONS WITH COMPLETE SOLUTIONS VERIFIED GRADED A+
$ 7.5

PEARSON RBT EXAM QUESTIONS AND ANSWERS .PEARSON RBT EXAM QUESTIONS AND ANSWERS .PEARSON RBT EXAM QUESTIONS AND ANSWERS .PEARSON RBT EXAM QUESTIONS AND ANSWERS .
$ 12
OMIS 430 Exam 1 homework Questions and Answers EXAM 1
$ 10

CWB Welding Inspector Exam (Latest Update) Questions and Verified Answers (100% Correct Grade A)
$ 12

2023 AQA AS ECONOMICS 7135/2 Paper 2 The National Economy in a Global Context Question Paper & Mark scheme (Merged) June 2023 [VERIFIED]
$ 7

POTTER PERRY & STOCKERT HALL'S 11TH EDITION TESTBANK FOR FUNDAMENTALS OF NURSING, A COMPLETE GUIDE
$ 14.5

COMM 309: Introduction to Mass Media Effects EXAM REVIEW
$ 4

Texas Boater Education Certification Exam Review: Texas Boater Education Certification Exam; Questions & Answers: Updated
$ 7.5

ATI questions PEDs exam 2. Commonly tested questions with Accurate answers.
$ 10

HESI PEDIATRIC QUESTIONS AND ANSWERS
$ 20.5

Pharmacology Midterm Exam
$ 12

GOVT 2306 / State and Local Government (Texas A&M University) – Healthcare Policy & Insurance Challenges in the U.S.: Analysis and Perspectives | Verified Study Notes | 100% Accurate | Grade A
$ 10

PCI ISA Exam Question 60 and answers 2022
$ 7

SLS 1122 Purpose Paper
$ 2

BIO 2301 Exam 3 Review Sheet (CO – Acid / Base) Cardiovascular Physiology Continued