ISYE 6501 – Intro Analytics Modeling
Due Date: 1/22/20
Homework 2
Question 3.1
Using the same data set...as in Question 2.2, use the ksvm or kknn function to find a good
classifier:
a) using cross-validation (do th
...
ISYE 6501 – Intro Analytics Modeling
Due Date: 1/22/20
Homework 2
Question 3.1
Using the same data set...as in Question 2.2, use the ksvm or kknn function to find a good
classifier:
a) using cross-validation (do this for the k-nearest-neighbors model; SVM is optional); and
Code for 3.1a is in the file named "3_1a_final.R".
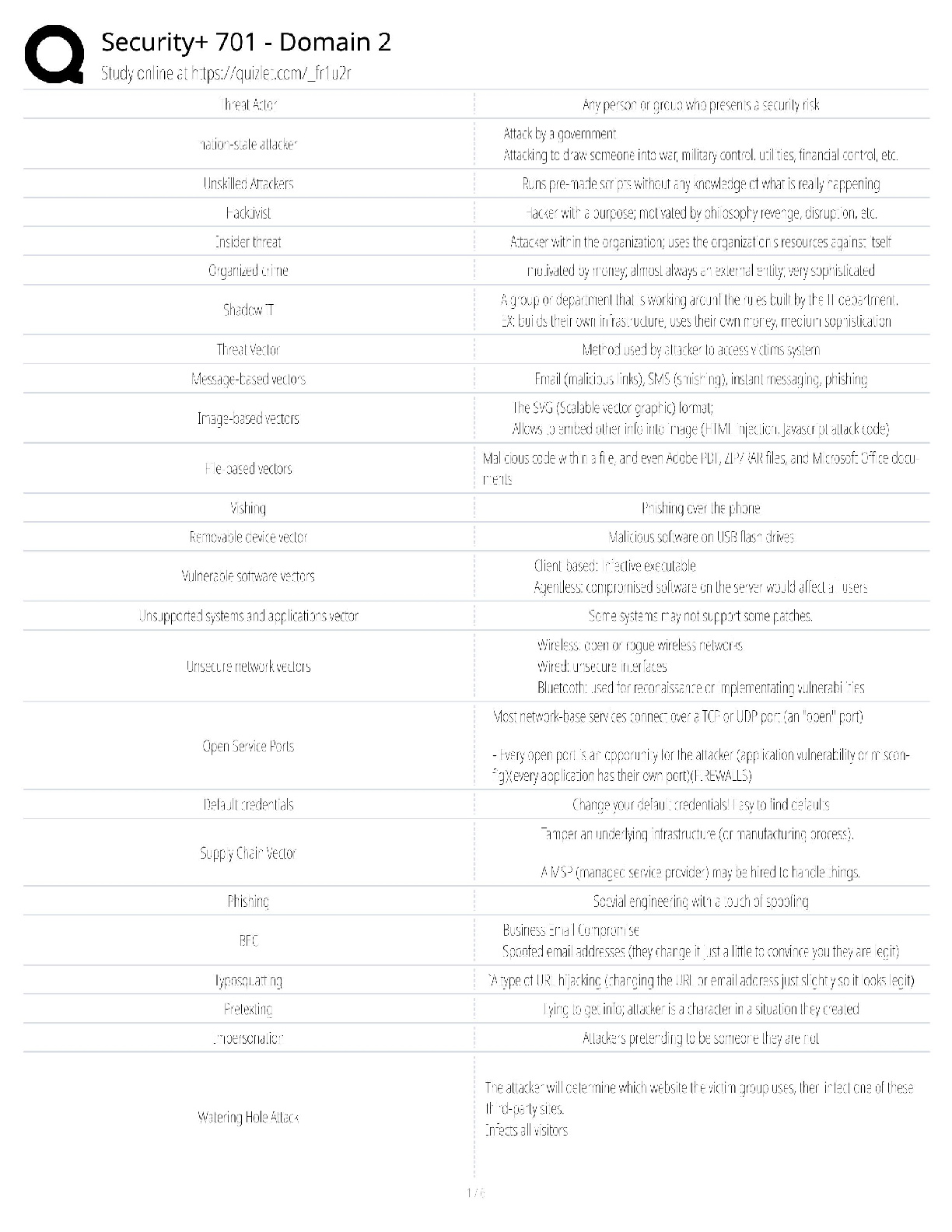
For the k-nearest-neighbors model, the highest accuracy was achieved using 5 as the 'k' value. The
plot below shows cross-validated model accuracties for k values from 1 to 30. I split the data 80%
for cross-validation and 20% for testing.
During cross-validation, the model with k=5 achieved an accuracy of 85.5%. Testing the model of
k=5 on the remaining 20% test data set resulted in an accuracy of 83.1%.
b) splitting the data into training, validation, and test data sets (pick either KNN or SVM; the
other is optional).
Code for 3.1b is in the file named "3_1b_final.R"
I chose to split the data 60% train, 20% validate, and 20% test. In the validation stage, I tested k
values from 1 to 30. Unlike the cross validation exercise completed in part a, maximum accuracy
was not achieved until 12 (84.7%). I'm not sure why k=5 resulted in a much lower 79.4% when
using train/validate/test. There are always both real and random effects. It's possible that some
This study source was downloaded by 100000842525582 from CourseHero.com on 05-13-2022 05:30:22 GMT -05:00
https://www.coursehero.com/file/55956553/HW2-ISYE6501-Submissionpdf/
random effects resulted in the higher k-values with artificially strong accuracies.
When I tested the model with k=12 on the remaining 20% of data, the accuracy was 87.0%, better
than the accuracy of k=5 reported in part A.
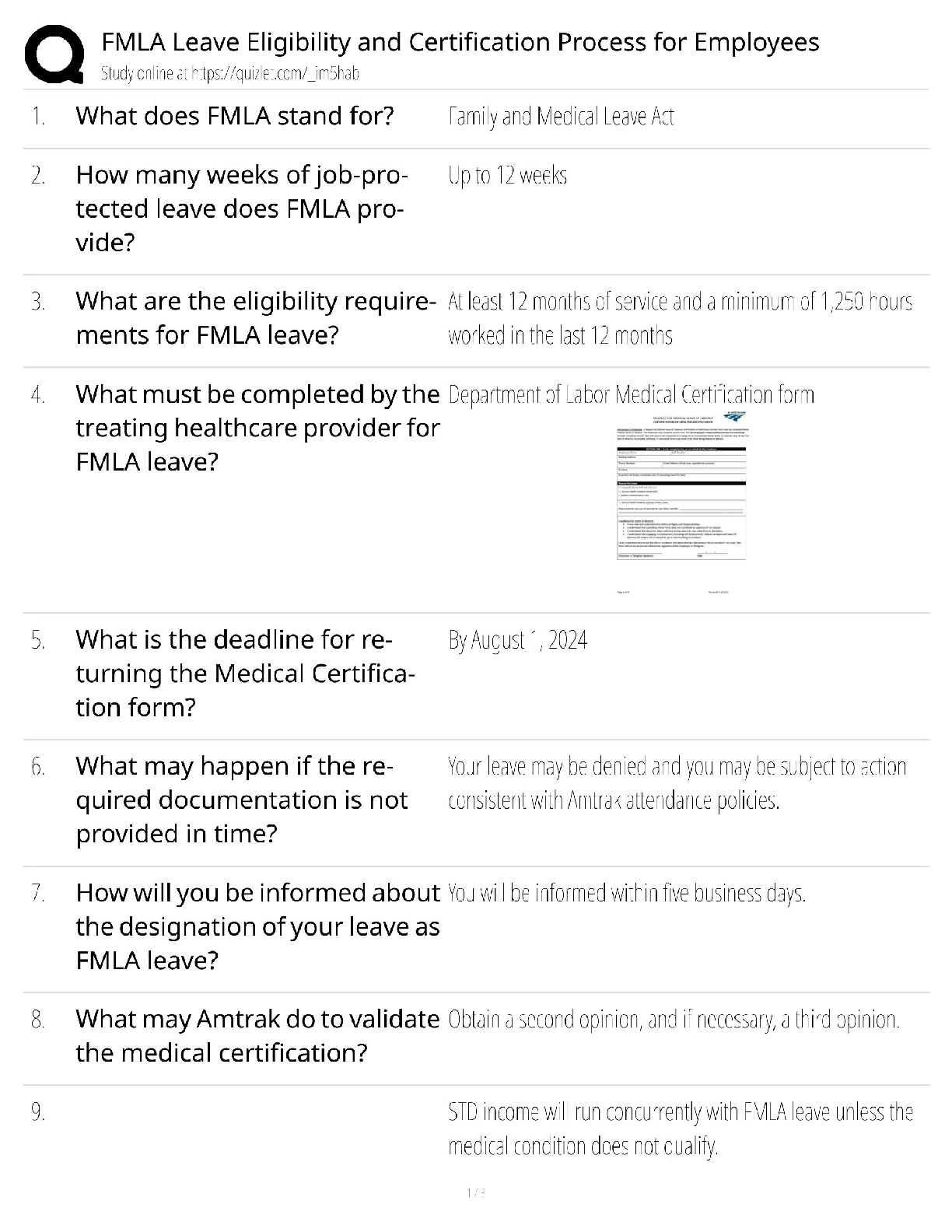
The plot below shows the accuracies of the different values of k. Unlike for cross validation, the
accuracy rises steadily from 5 to 8. The difference in accuracy above 8 does not appear to change
significantly. If this were an elbow plot, I think that k=8 would be a reasonable choice for lowest k
value that provides the highest accuracy.
Question 4.1
Describe a situation or problem from your job, everyday life, current events, etc., for which a
clustering model would be appropriate. List some (up to 5) predictors that you might use.
I work as a chemical process engineer at an oil refinery. One of the units that I monitor is the
Alkylation Unit. Alkylation is a process that converts LPG (Liquefied Petroleum Gas) into highoctane gasoline using an acid catalyst. One undesirable byproduct that is produced is called Acid
Soluble Oil (ASO). The reaction mechanism to make ASO is complex, and operating conditions vary
day by day. However, there are some days or weeks when ASO production is particularly high.
There is not one single set of conditions that produces high amounts of ASO.
Clustering could be useful because days of high ASO production could be grouped together, and
then the conditions that lead to high ASO production could be analyzed. The data would then be
used to avoid operating conditions that lead to high ASO production. One of the great things about
refineries is that there are myriad temperature, pressure, level, and flow indications that are
constantly being measured and recorded. Also, lab samples are taken frequently, and all of that dat
a is also available for analysis. For the clustering model, I would select at least the following five
components:
This study source was downloaded by 100000842525582 from CourseHero.com on 05-13-2022 05:30:22 GMT -05:00
https://www.coursehero.com/file/55956553/HW2-ISYE6501-Submissionpdf/
1. Alky Unit charge rate (feed rate to the unit).
2. Ambient temperature (reaction is highly temperature dependent).
3. Acid riser temperature (effectively the reactor temperature).
4. Concentration of C5 or heavier in the Alky feed (daily lab test).
5. Flow rate of the settler effluent recycle.
Question 4.2
Use the R function kmeans to cluster the points as well as possible. Report the best combination
of predictors, your suggested value of k, and how well your best clustering predicts flower type.
Code for 4.2 is found in "4_2_final.R"
Surprisingly, I found the best combination of predictors to be a single predictor. Using only petal
width, the clustering model (with k = 3) acheived an accuracy of 96%. This means, that for the 150
data point set, there were only six misclassified points. For a combination of multiple predictors,
using sepal width, petal length, and petal width resulted in an accuracy of 94%. This was slightly
unexpected, because the least accurate single predictor model used sepal width (only 56% model
accuracy). However, excluding sepal length resulted in the highest accuracy for any combination of
the three predictors.
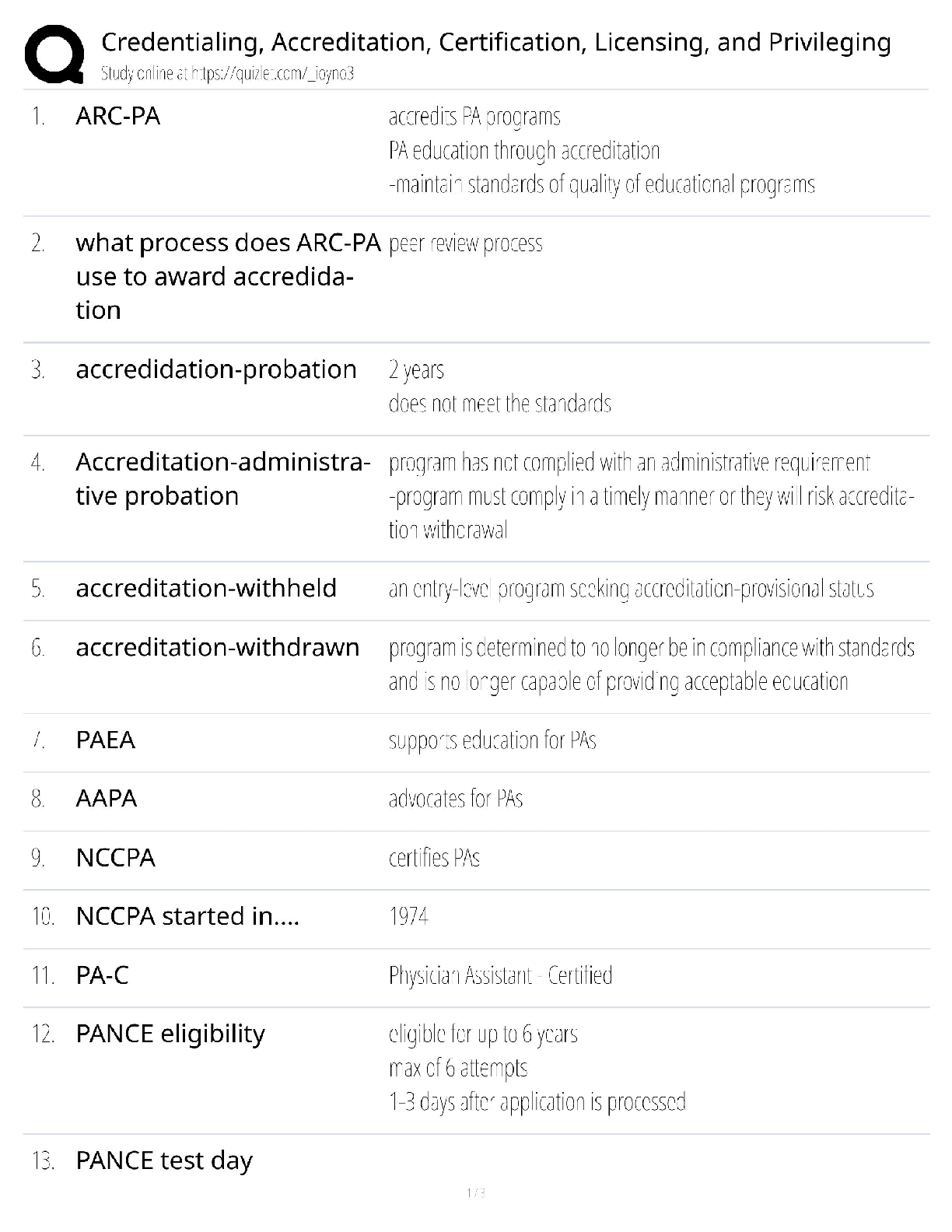
I decided on using a value of k = 3 by making an elbow plot of the total of sum squared distance
within clusters versus k (number of clusters). The 'elbow' consistently appeared at 3 for all highaccuracy models. For some of the lower-accuracy models, the elbow appeared to shift towards a
higher number of clusters. The elbow plot is included below. This particular elbow plot was
produced using all four predictors (accuracy = 89.3%
[Show More]