
NRNP 6560 Midterm exam with complete solutions
$ 10

REVIEWED 2024 PEDIATRIC NURSING COMPREHENSIVE EXAM 2022-2023 WITH CORRECT ANSWERS [COMPLETE EXAM IS IN SCREENSHOTS FORMAT]
$ 17

SAFe Scrum Master Practice Test 2022 with complete solution
$ 6
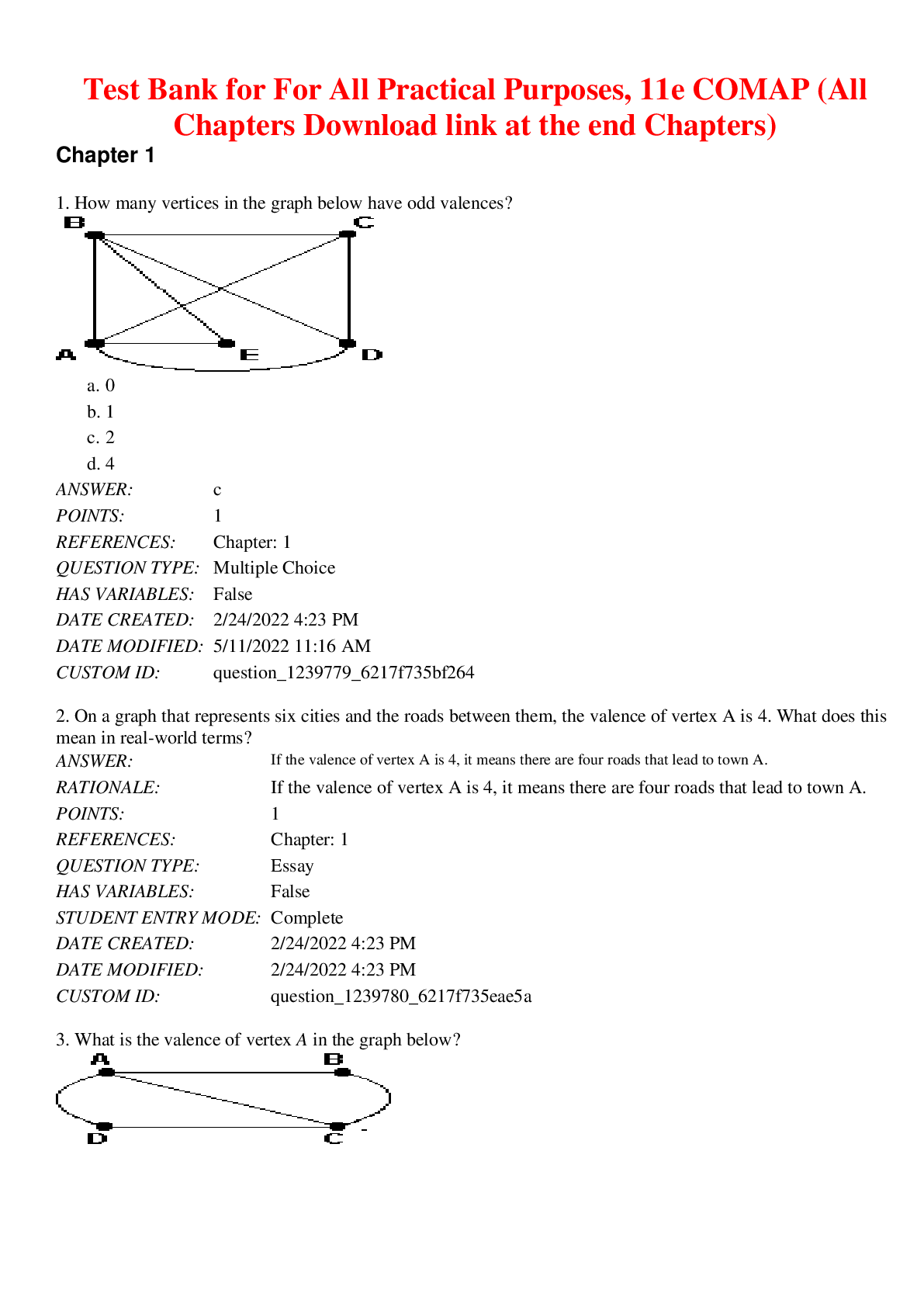
Test Bank for For All Practical Purposes, 11th Edition By COMAP
$ 29

CFT Monitor USMC Exam Questions | 100% Correct Answers | Expert Verified | 2025/2026 Edition
$ 7.5

microeconomics-hd-quality-exam-summary-notes-ecf1100.
$ 12

HEALTH SYSTEMS MANAGEMENT
$ 4

PED 200 QUIZ 1 AND 3 UPDATED QUESTIONS AND ACCURATE ANSWERS 2024-2025 VERIFIED
$ 9.5

Centennial High SchoolMATH Pure Mathmath_performance_task_unit1-REVIEWED BY EXPERTS 2021
$ 6.5

ATI med surg assessment 2023-2024
$ 7

Psychology 101 - Week 5
$ 12.5

ICT 380 - Security Master Plan Presentation Murdoch University ICT 380
$ 8

4A051 CDC URE Questions
$ 11

Civil Service Exam- Practice Test #2
$ 7

Pearson Edexcel International GCSE In Pakistan Studies (4PA1) Paper 02 Mark Scheme Summer 2021 (Provisional)
$ 5
BCBA Mock Exam 1 5th Edition Task List | 160 Questions | 5th Edition Task List | Board Certified Behavior Analyst | BCBA Exam Prep | BCBA
$ 20

AMMO 49 EXAM 2025| BRAND NEW ACTUAL EXAM WITH 100% VERIFIED QUESTIONS AND CORRECT SOLUTIONS| GUARANTEED VALUE PACK| ACE YOUR GRADES.
$ 6

Henke's Med-Math Dosage Calculation, Preparation, & Administration 9th Edition by Susan Buchholz TEST BANK
$ 24

Summary RNSG 1215 HA Exam 1 Study Guide
$ 7.5

NCLEX-RN SAFETY AND INFECTION CONTROL EXAM PART 2 2023
$ 6.5

GFEBS ESSENTIALS SUBSUMES L101E L201E L303E 2023/2024 EXAM STUDY QUESTIONS WITH VERIFIED ANSWERS GUARANTEED PASS | RATED A+
$ 12.5

Sophia Intro to Sociology Unit 4 Milestone 4
$ 15

AZ 104 Renewal Exam Questions Answers New 2023 Verified Answers
$ 16

C841 Task 1 Template (IHP4)
$ 11

APEA_PREDICTOR_EXAM_LATEST_EXAM_2024_2025_ALL_900+_QUESTIONS_AND
$ 15

Texas Food Manager Certification / ANSI-CFP Exam Study Guide / 2025 Test Bank & Practice Exam
$ 20

NCTI PARAMEDIC PHARMACOLOGY TRADE NAMES EXAM TEST WITH 100% CORRECT QUESTIONS AND ANSWERS
$ 13

Copy of Centripetal Acceleration Lab PHY 11
$ 8

eBook Laser Inter-Satellite Links Technology 1st Edition By Jianjun Zhang Jing Li
$ 30

C841 Task 1 Template (IHP4)
$ 11

NR442 - RN Community Health Exam 2 ALL ANSWERS 100% CORRECT SPRING FALL-2022 LATEST GUARANTEED GRADE A+
$ 11

eBook [PDF] Culture Wars in America An Encyclopedia of Issues, Viewpoints, and Voices 2nd Edition By Roger Chapman, James Ciment
$ 27

BENEFITS OF WILDLIFE
$ 10

Exam ISSA Final Exam ALL ANSWERS 100%
$ 5

CANADIAN AND FEDERAL INCOME TAXATION PRACTICE 100+ DETAILED QUESTIONS WITH CORRECT ANSWERS 2023-2024
$ 16

A&P II Exam Module 2 EXAM elaborations (100% CORRECT SOLUTIONS)
$ 14

NSG 6420 FINAL EXAM 20232024


























