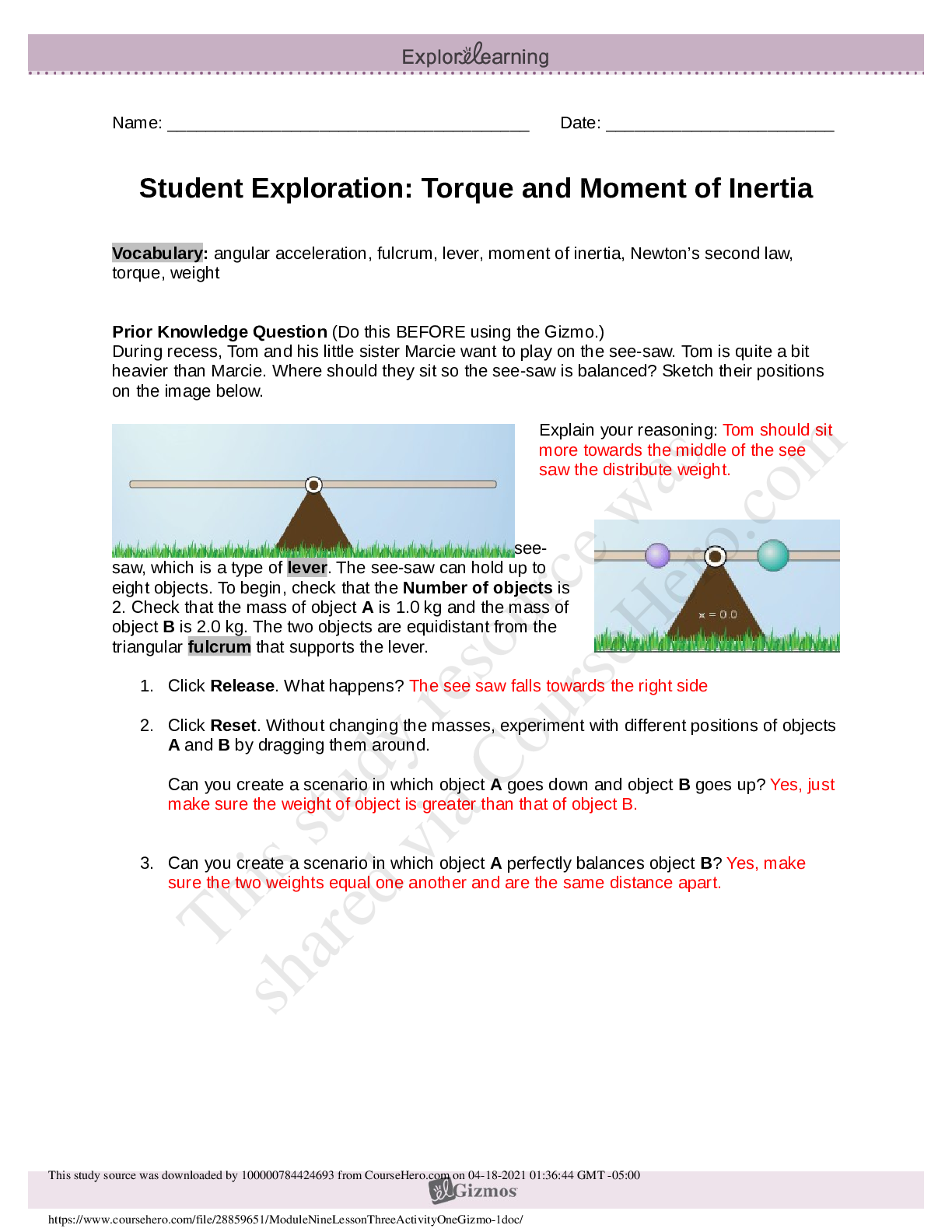
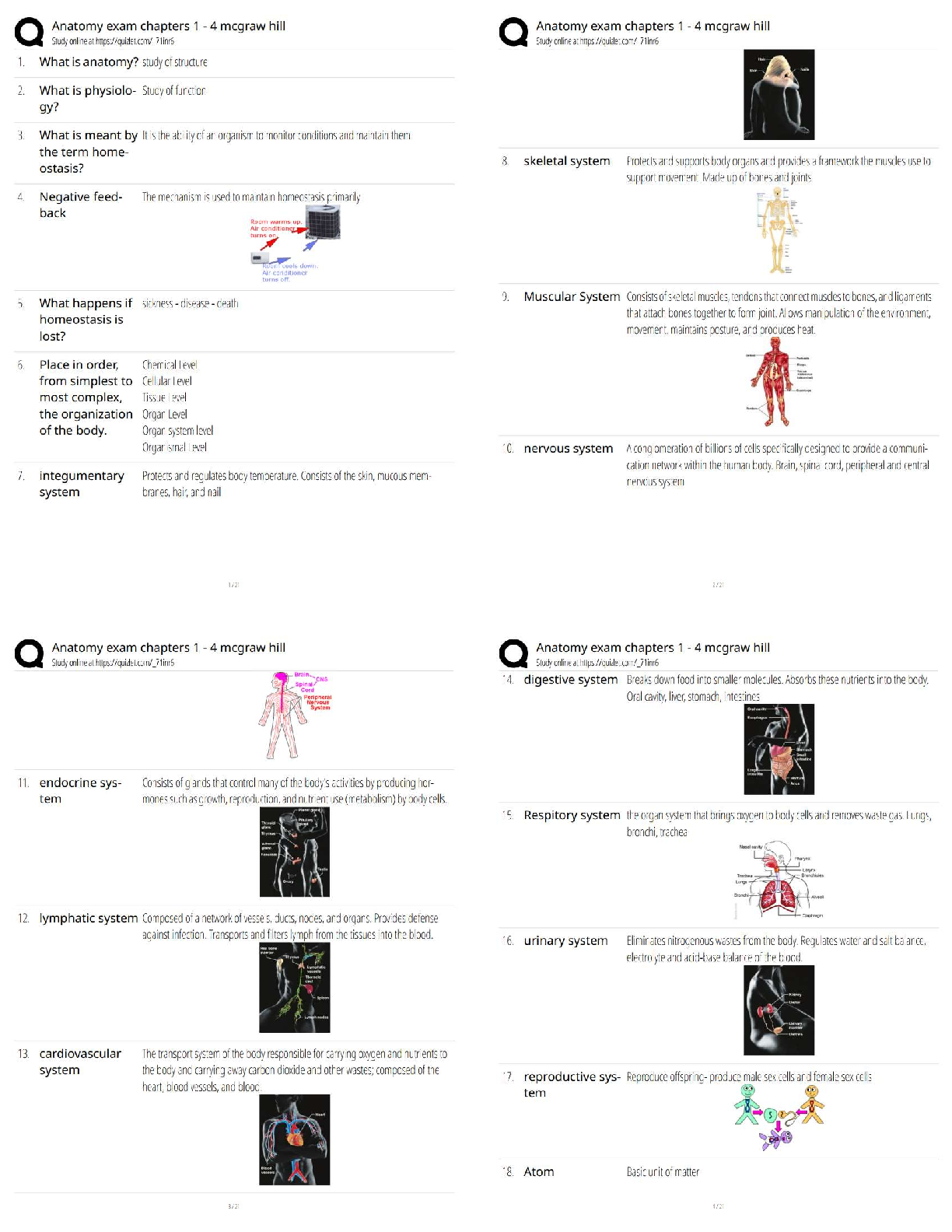
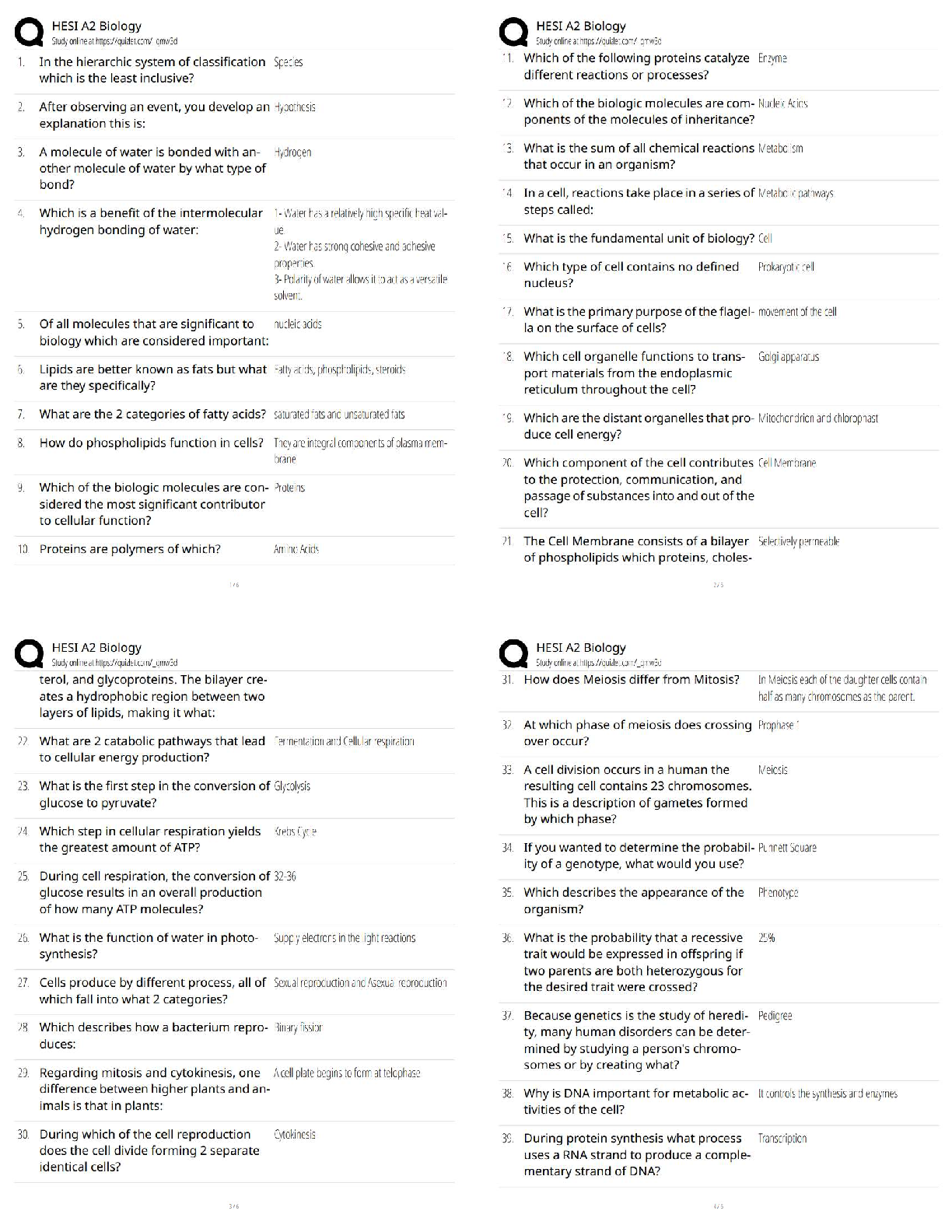
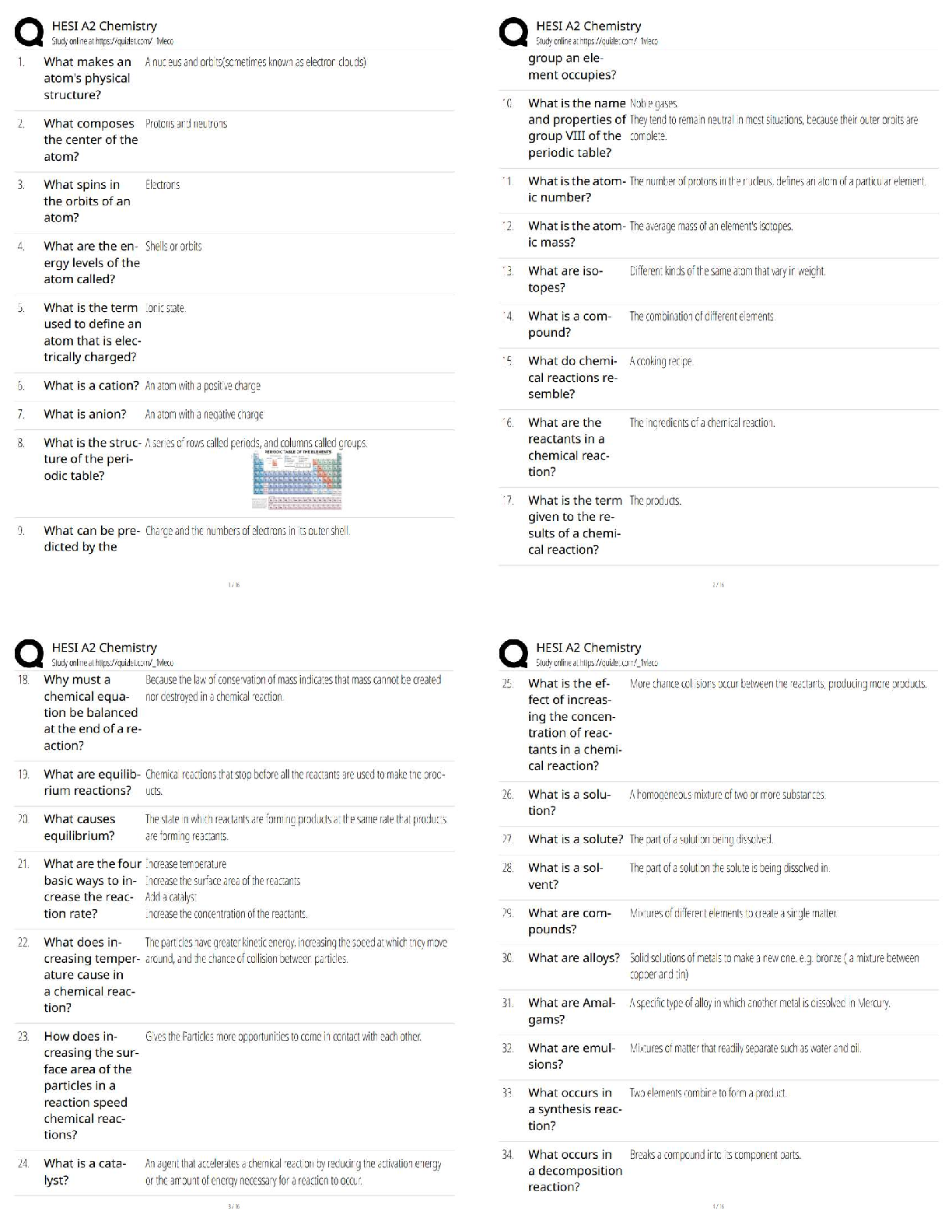
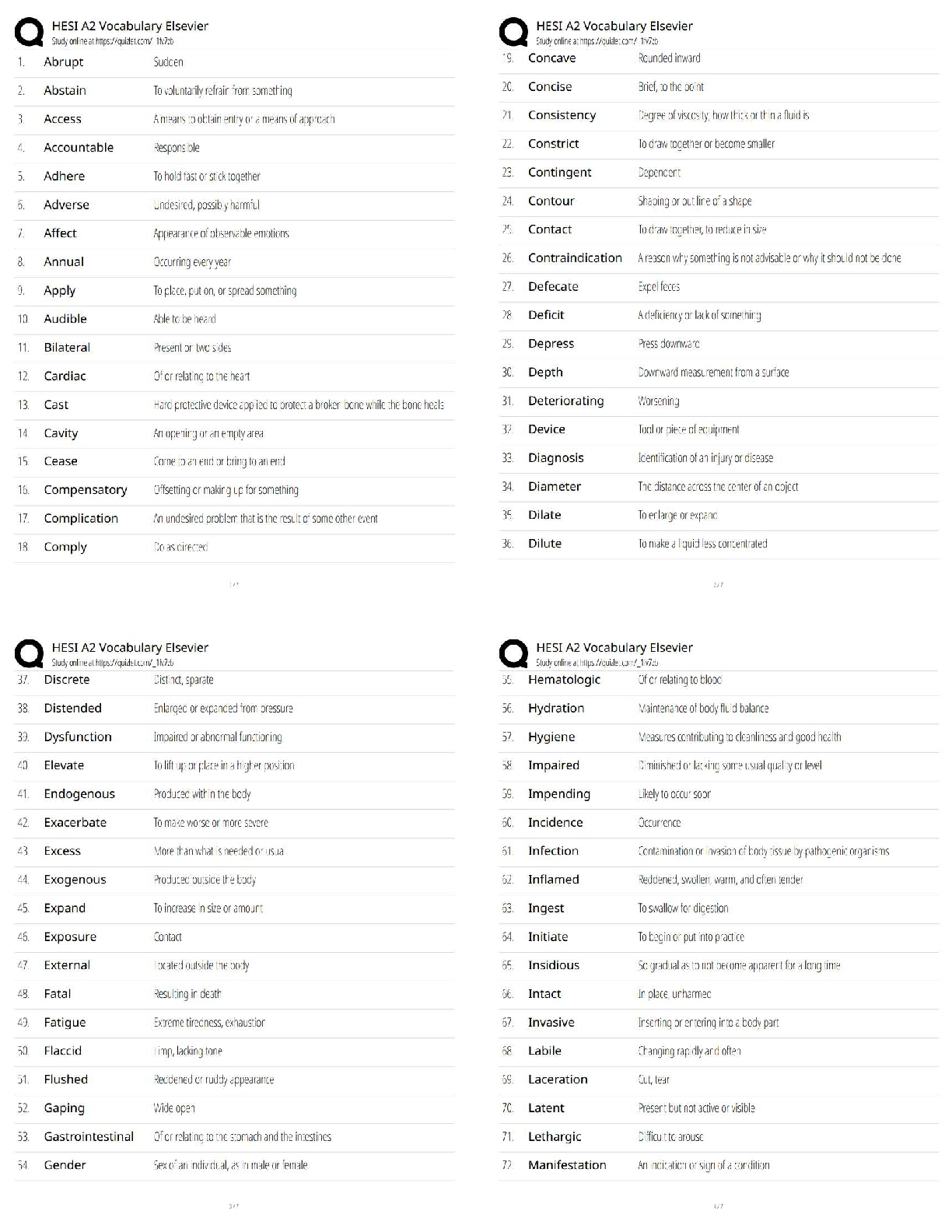
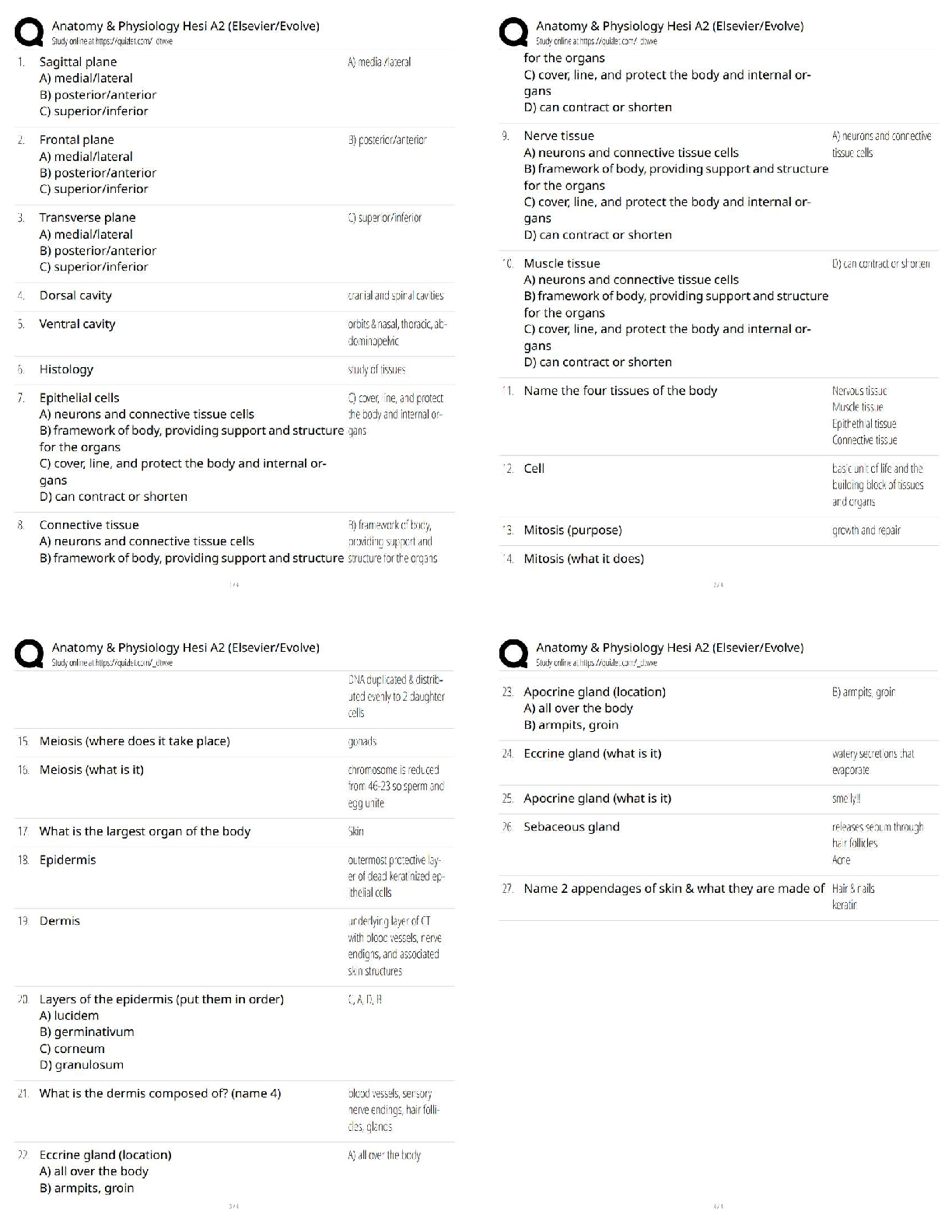
SOCS 315 Week 7 Homework Assignment: Chapter 12, 13 & 14 Questions
$ 12

Test bank for human development a life ...tion robert v kail john c cavanaug
$ 30.5

ISSA NUTRITIONIST CERTIFICATION SUPPLEMENTATION Q & A 2024
$ 13

eBook [PDF] Pratt's Long Term Care Managing Across the Continuum 5th Edition By Steven Chies
$ 30

2023 BIOD 151 ANATOMY AND PHYSIOLOGY 1 PORTAGE LEARNING ALL EXAMS
$ 18.5

Mark Scheme (Results) Physics (9PH0) Paper 2: Advanced Physics II November 2021 Pearson Edexcel GCE
$ 10

Computer_Study_265_Week_5_Assignment Latest 2021
$ 13.5

eBook PDF for Introduction to Data Analytics For Accounting 2nd Edition By Vernon Richardson, Katie Terrell and Ryan Teeter
$ 29
Betty Burns Part 1 V3 PC -K (Basic DDx) 48 years 5' 6"
$ 7
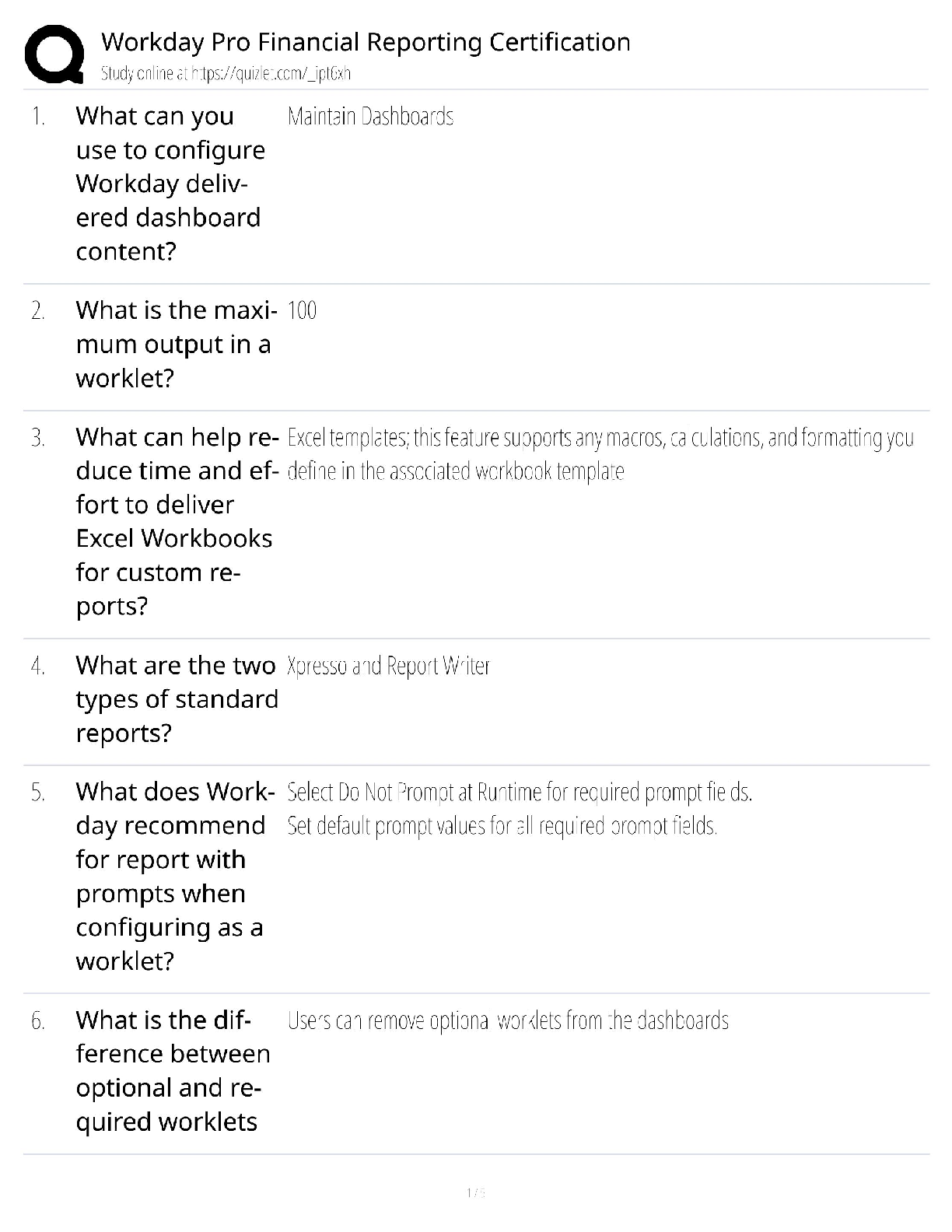
ACCT 515 Workday Pro Financial Reporting Certification / Study Guide & Test Bank / 2025 ERP Update / Score 100%
$ 21

National Check Payments Certification NCP Test Bank / Check Processing Exam / 2025 Update / Score 100%
$ 21.5

TICO General Questions Modules 4
$ 11

ENGLISH 11- FULL PRACTICE QUESTIONS FOR EXAMS
$ 4.5

NUR2459 / NUR 2459: Final Exam Lecture Notes Updated Mental and Behavioral Health Nursing - Rasmussen
$ 9

WGU D430 Fundamentals of Information Security Final Exam and Practice Exam 2024 Actual Exams with 500 Questions and Correct Detailed AnswersA+ Grade
$ 15

Instructor Manual For Foundations of Physical Education, Instructor Manual For Exercise Science, and Sport 21st Edition By Deborah Wuest Jennifer Walton-Fisette ( All Chapters, 100% Original Verified, A+ Grade)
$ 30

The Diary of a CEO: The 33 Laws of Business and Life by Steven Bartlett
$ 4.5

Week #3: Assignment: Assessing, Diagnosing, and Treating Conditions of the Cardiovascular System 1 (NRNP 6550: Advanced Care of Adults in Acute Settings II) i-Human: Darrell Bridges V5.1







.png)