eBook PDF for Paramedic Pocketbook of Prescription Medications 1st Edition By Rose Matheson

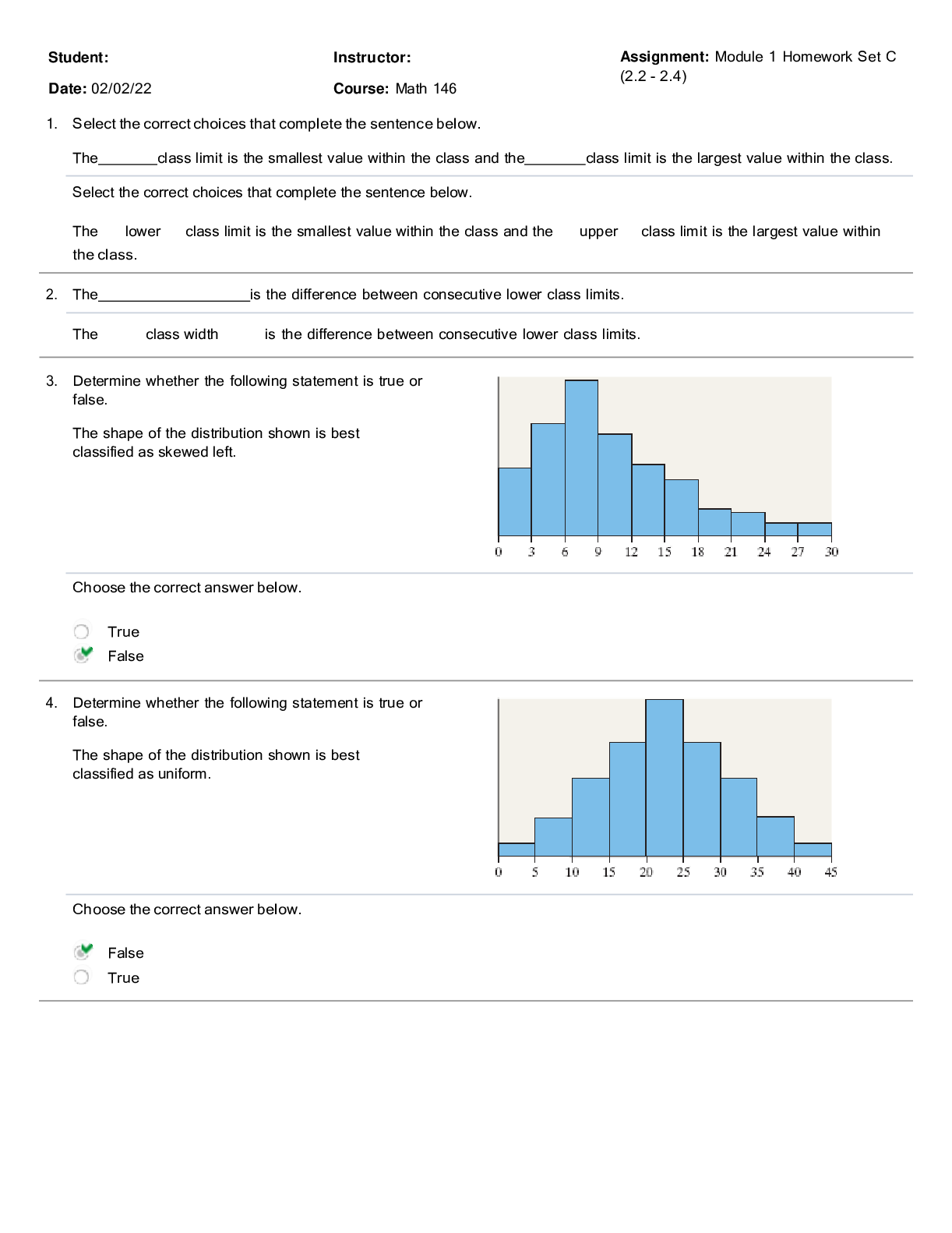
$ 25

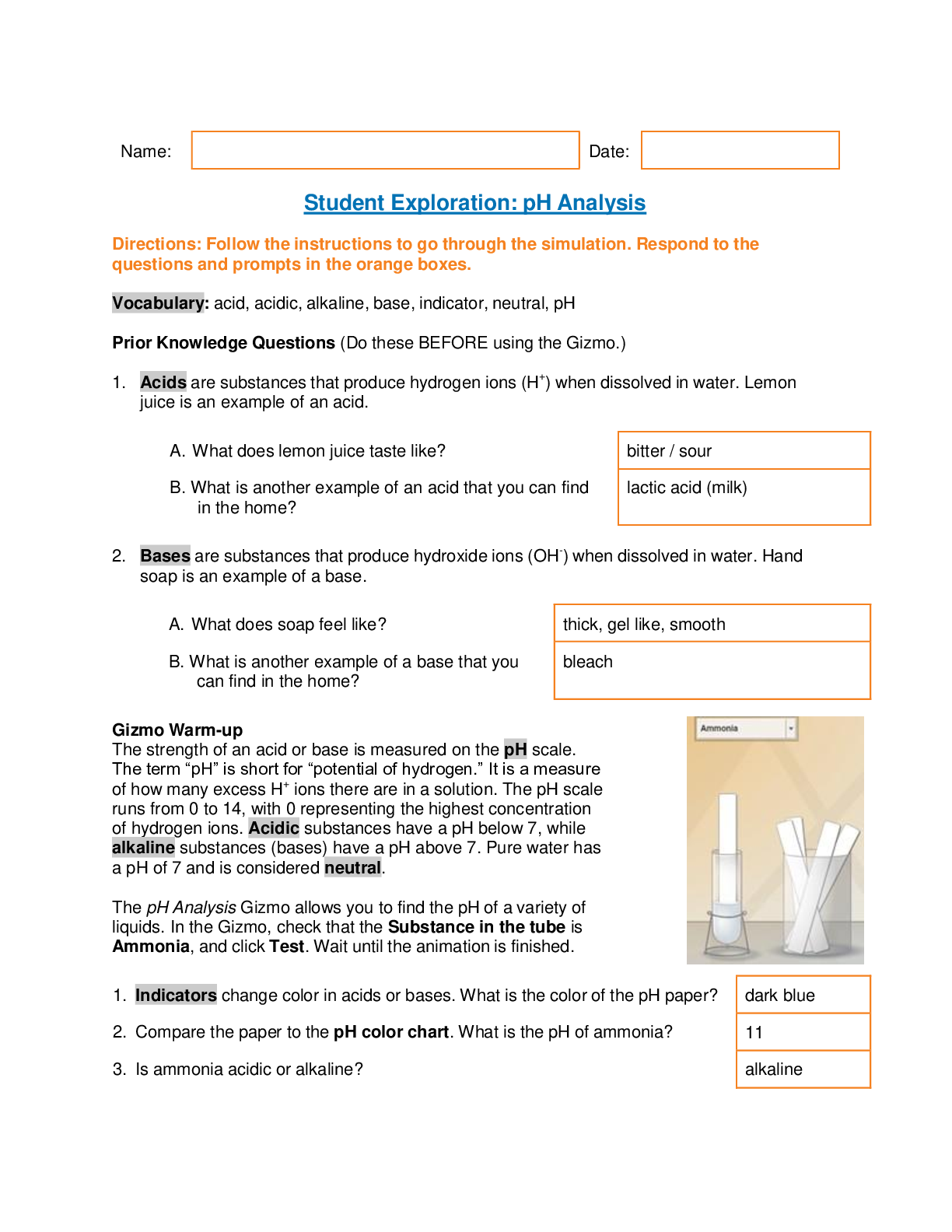
pH Analysis Questions and Answers

$ 7

MA278 / BSC2346 Section 06 Human Anatomy and Physiology I Final Exam, attempt Score: 59 Out of 60.

$ 20

eBook Robotic Surgery for Renal Cancer 1st Edition By Sanchia S. Goonewardene , Raj Persad ,David Albala

$ 25

Solutions Manual For Essentials of Econometrics, 5th Edition By Damodar Gujarati, Dawn Porter

$ 30

A Level Ancient History_H407/12 Mark Scheme Oct 2021 | Athens and the Greek world

$ 7

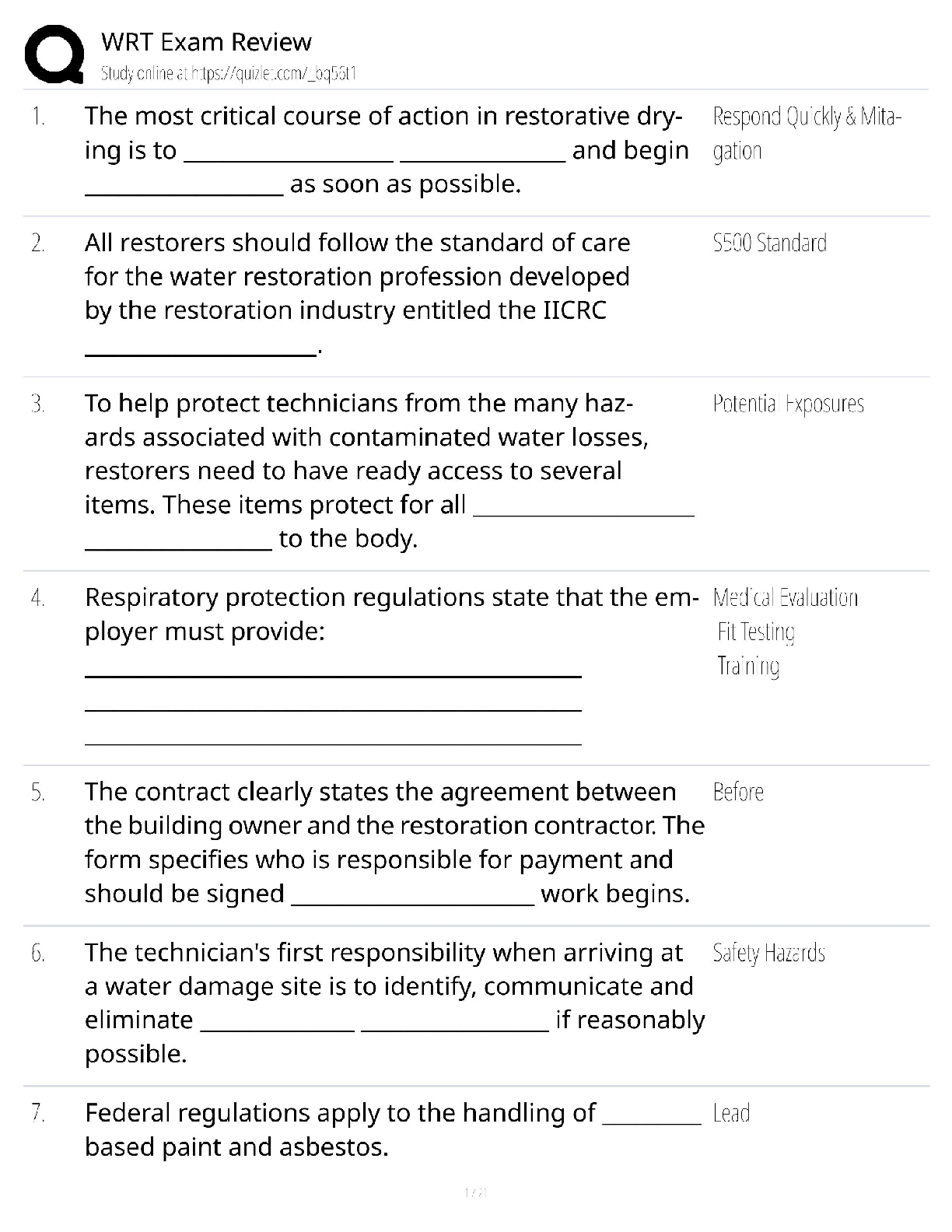
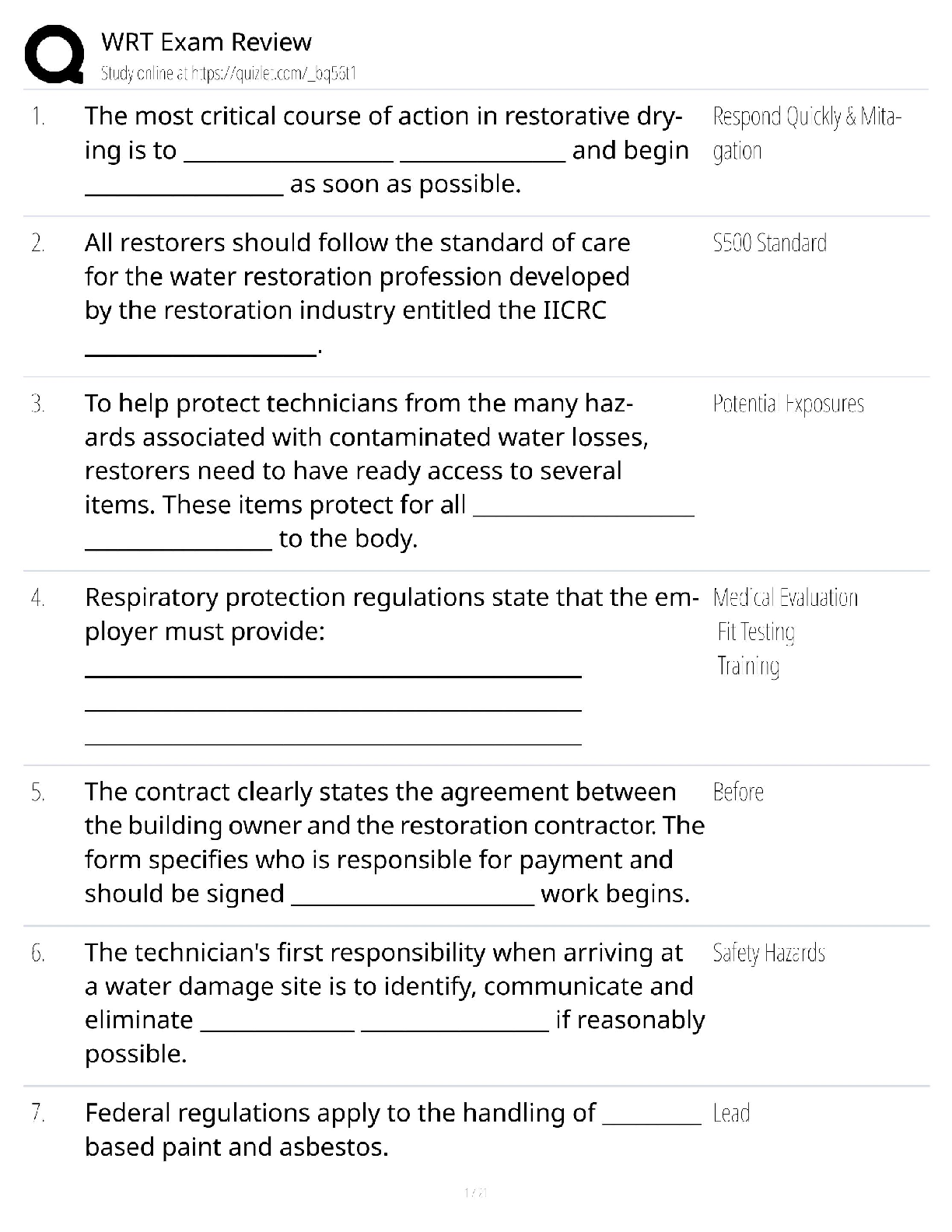
WGU C207 Data Driven Decision Making Module 2 Latest 2023 Rated A

$ 10

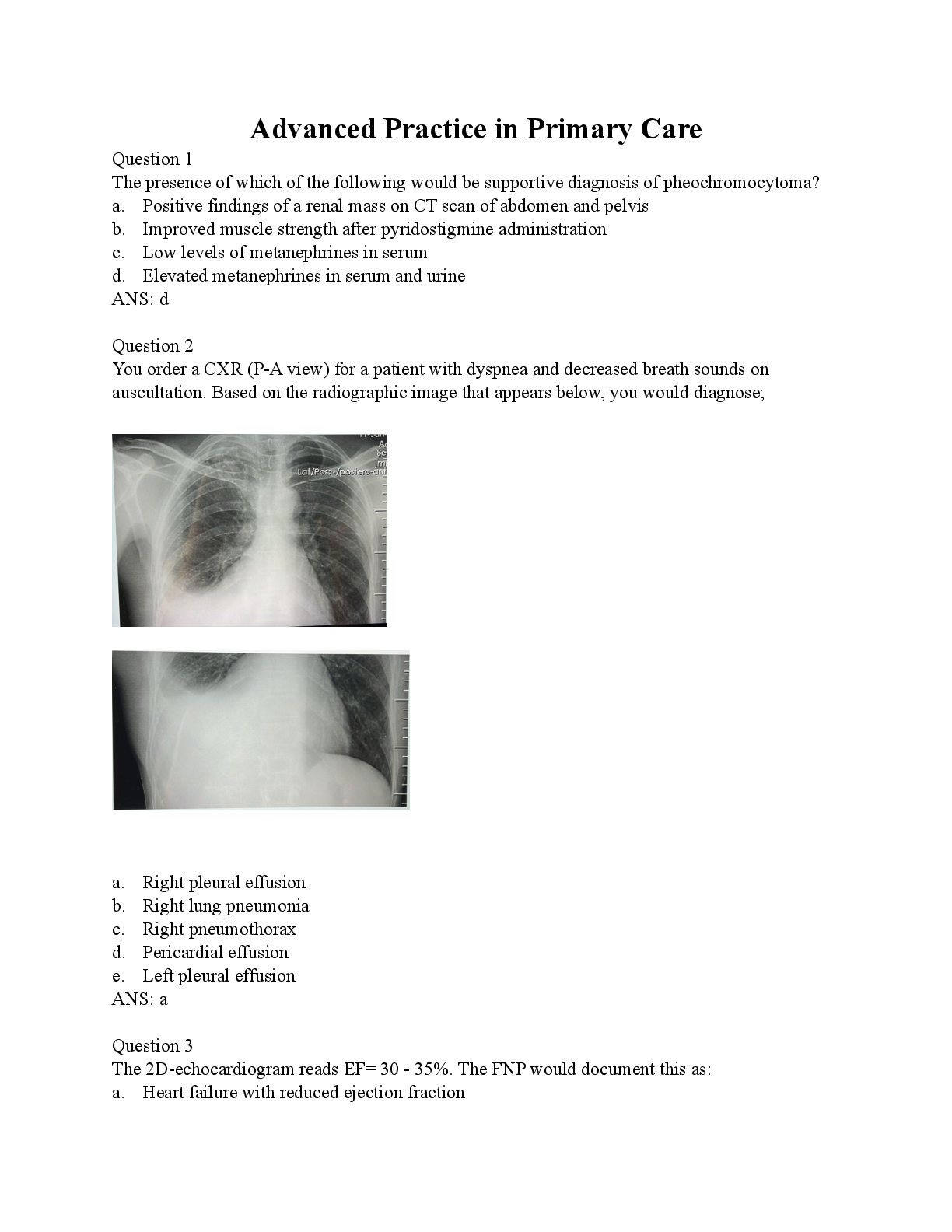
Miami Regional University: Advanced Practice in Primary Care Exam Questions with Answers 2025

$ 41

Edexcel A Level In GCE Physics (9PH0/01)Paper 1: physics I + mark scheme May 2025

$ 10

Sophia Final Milestone,100% CORRECT

$ 15

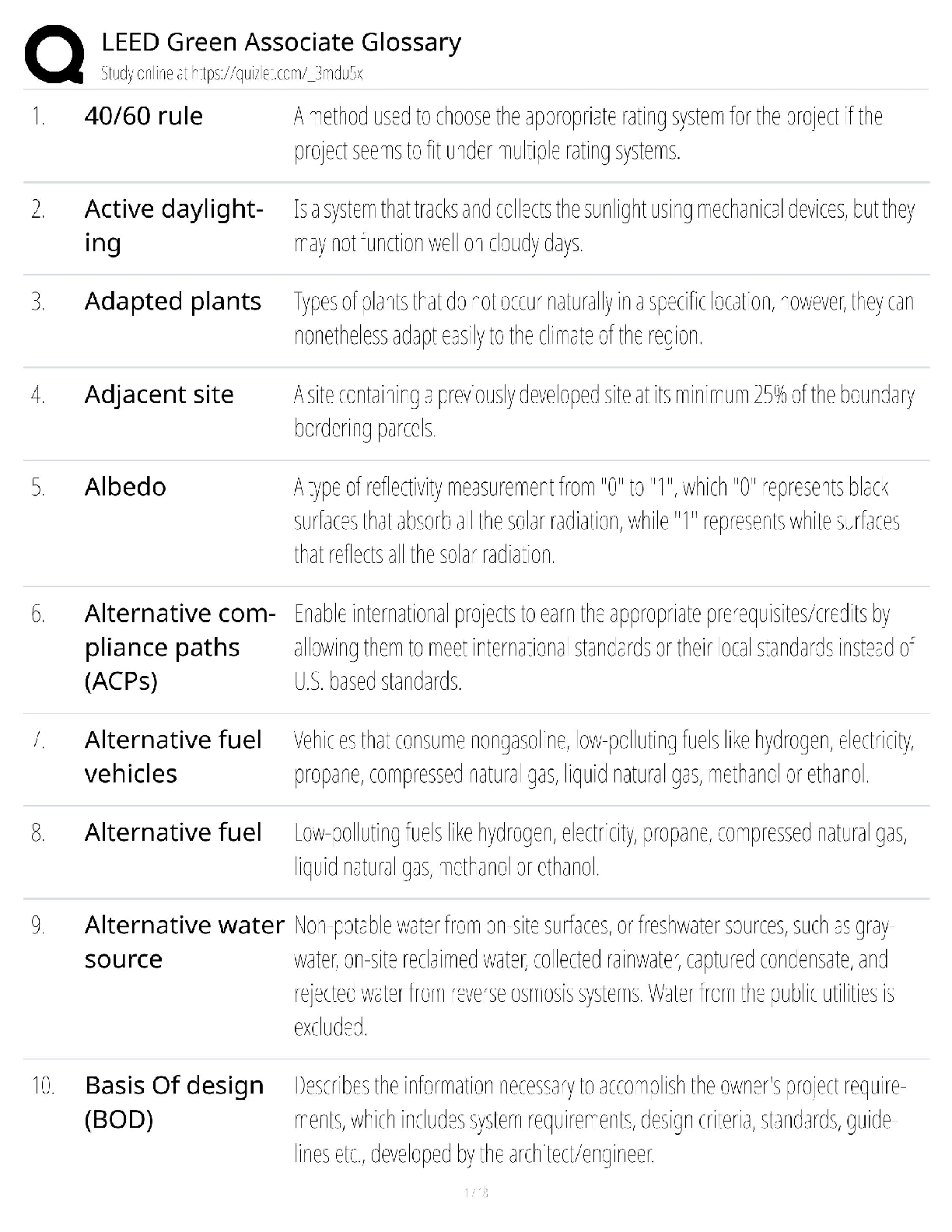
eBook PDF Child Development An Introduction 15th Edition By John Santrock, Kirby Deater-Deckard, Jennifer Lansford

$ 30

WGU Project Management C722 Unit 8 Questions and answers, graded A+. A quality audit should______________.

$ 9

Test Bank for Foundations of Earth Science, 8e Frederick Lutgens, Edward Tarbuck, Dennis Tasa (All Chapters)

$ 7.5

eBook (EPUB) [PDF] Introduction to Teaching 4th Edition By Gene Erwin Hall, Linda Quinn, Donna Gollnick

$ 30

University of the West Indies at St. Augustine - BIOC 2169BIOC2169-DNA Lab 2020 -STUDENT LAB-1 (1).

$ 7

Florida Civic Literacy Exam (FCLE) Practice Exam - Q & A

$ 12

NCLEX-RN EXAM PREP 2023/2024 | 75 QUESTIONS, ANSWERS AND EXPLANATIONS

$ 15

CJ 215 CRIMINAL JUSTICE (CRISIS INERVENTION) LATEST REVIEW FINAL EXAM Q & A 2024

$ 13

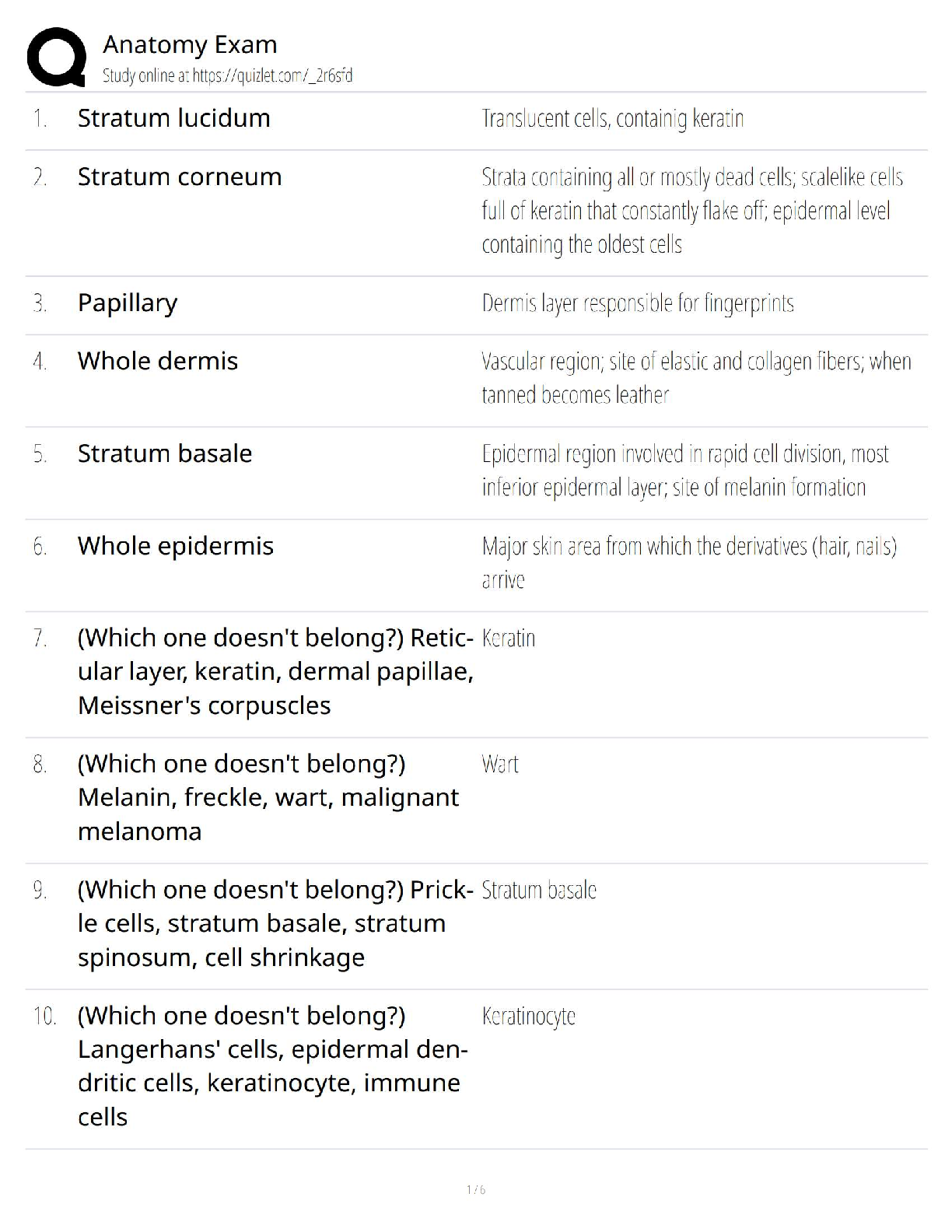
Anatomy Exam / Score 100% / 2025 Update / Test Bank, Study Notes & Practice Questions

$ 8.5

[eBook] [PDF] Osteoporosis Osteoarthritis and Rheumatoid Arthritis An Agonizing Skeletal Triad By Puneetpal Singh

$ 27

Salesforce Admin 201 Practice Exam Questions with Complete Solutions

$ 15

WISCONSIN_CIVICS_EXAM_QUESTIONS_&_ANSWERS_VERIFIED_LATEST_UPDATE

$ 15

Straighterline BIO 202L Lab 18 The Reproductive System Quiz 2022 | Complete | 100% Correct Answers

$ 5

2024 DMV Nevada Permit Test New Full TEST | Questions and Answers ( Included ) 100% Correct

$ 11

MN568 Unit 2 Exam : Kaplan University (graded A) {Latest 2019 Questions & Answers}

$ 21

eBook Protein Interactions The Molecular Basis of Interactomics 1st Edition By Volkhard Helms, Olga V. Kalinina

$ 30

ATI RN Comprehensive Predictor 2019 Test With Correct And Verified Answers

$ 38.5

SOPHIA PATHWAY- MACROECONOMICS Milestone 3

$ 10

BIO 235 midterm 2 version B Study Notes 2b study notes

$ 10.5

WGU D002- Professional, Ethical, and Legal Practices for Special Education Verified Solutions 100%

$ 10.5

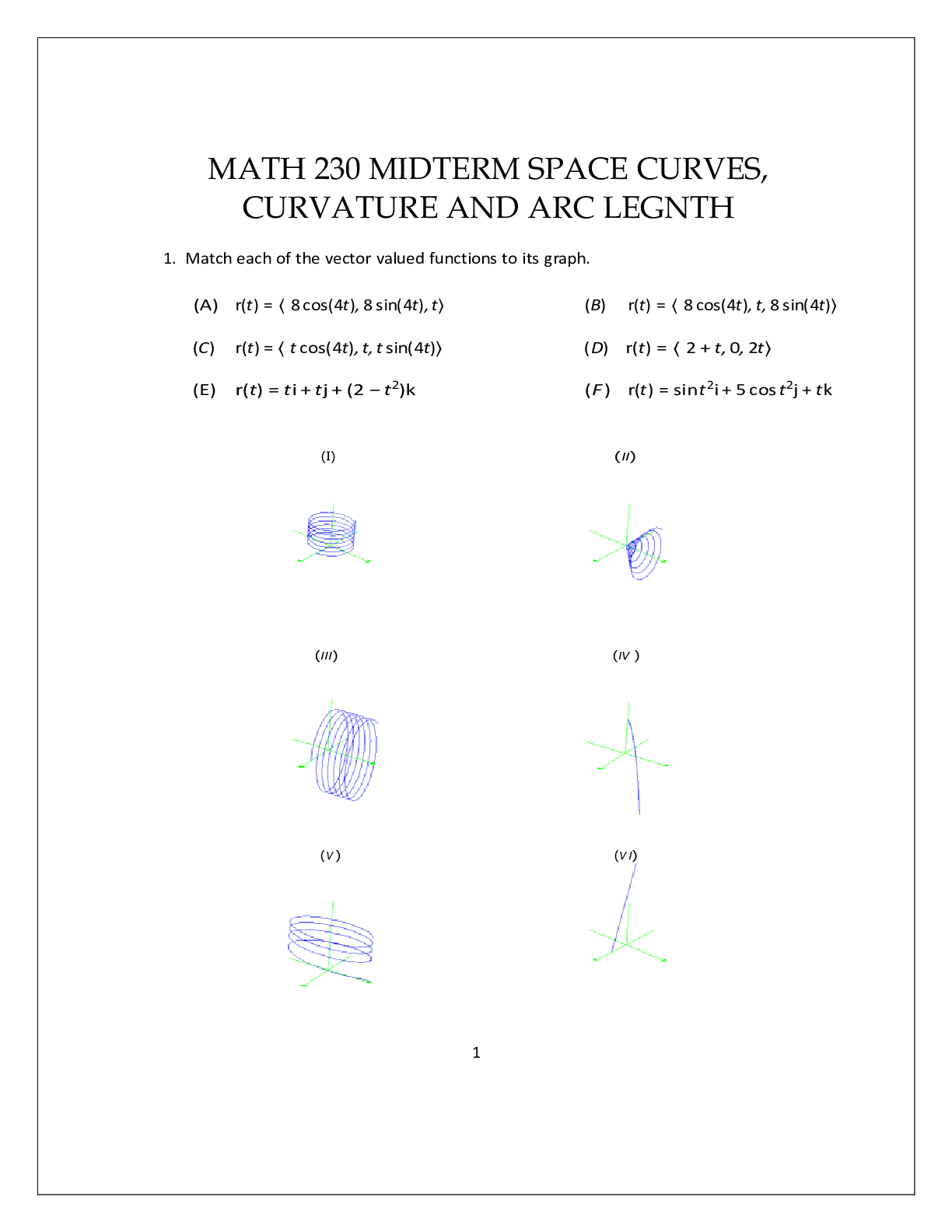
MATH 230 MIDTERM 1 SPACE CURVES, CURVATURE AND ARC LEGNTH OFFICIAL PRACTICE QUESTIONS 2024

$ 14

ECE Test Questions and answers, 100% Accurate, graded A+

$ 6

NR 503 Week 3 Discussion: Chronic Health and Occupational Health Articles

$ 10

University of PhoenixCJA 224Plea Bargaining Paper_Week 3

$ 9

SEJPME Lesson 5 Crisis Response and Limited Contingency-St John's University: Complete Solution 100% Correct

$ 15

MGT 6681 Quiz Review complete exam questions and answers solved solution

$ 13

Engineering > QUESTIONS & ANSWERS > Clemson University ECE 8010 ECE8010_HW4_solution. (All)

Clemson University ECE 8010 ECE8010_HW4_solution.

Document Content and Description Below

ECE 8010 Homework #4 Solutions 1. (Exercise) The elementary row operations used to find reduced row echelon form of a matrix are (i) scaling row i by  , (ii) swapping row i and row j, and (iii) replacing row i with the sum of row i and row j. a. Performing an elementary row operation on a matrix A is equivalent to multiplying A on the left by an appropriate square matrix M , i.e. MA. For each of the elementary row operations, describe the form of the matrix M and check that the matrix is full rank. b. Similarly, elementary column operations are equivalent to right multiplication by an appropriate square matrix M , i.e. AM . For each of the elementary column operation, describe the form of the matrix M and check that the matrix is full-rank. 2. (Exercise) Let :    n n  , :    n m  , :    m m  be linear transformations such that ( )   n and ( )   m . Use the Sylvester Inequality to show that   ( ) ( )    . 3. Let : n n A    , : m n B    , : m m C    be linear transformations. (The notation A B C , , will be used for the transformation as well as the corresponding matrix representation of the transformation when the standard bases are used for the domain and codomain.) Let A and C be full rank. a. Show that   ( ) ( ) AB B  b. Find a counterexample to demonstrate that in general   ( ) ( ) BC B  c. Show that   ( ) ( ) BC B  d. Find a counterexample to demonstrate that in general   ( ) ( ) AB B  e. (Exercise) Can you find a condition related to m , n , and ( ) B that will guarantee that the columns B form a basis for ( ) B ? Note that 3a is a stronger statement than   ( ) ( ) AB B  . While   ( ) ( ) AB B  implies   ( ) ( ) AB B  , the converse is not true. Similarly for 4b,   ( ) ( ) BC B  implies   ( ) ( ) BC B  , but the converse is not true. 4. (Exercise) True/False: (Provide a proof if true, or a counterexample if false.) a. A full rank linear transformation is always onto. b. A full rank linear transformation is always 1:1. c. A square, full rank linear transformation is always 1:1

[Show More]

Last updated: 3 years ago

Preview 1 out of 14 pages

Buy Now

Instant download

We Accept: